第109页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
8.(2025·南通如皋期末)小明同学骑自行车上学途中,要经过一段上坡路。他思考:物体以相同初速度冲上斜坡后运动的最大距离可能与哪些因素有关呢?他和小华商量后提出以下猜想。
猜想一:可能与斜坡的粗糙程度有关;
猜想二:可能与物体的质量大小有关;
猜想三:可能与斜坡的倾角大小有关。
他们将与水平面平滑连接的长木板以角度θ(可改变)倾斜固定,并找来质量不同的小木块若干、光滑的斜面M(物块在斜面M上滑动时可忽略物块所受的摩擦力)和轻弹簧P等实验器材进行探究。
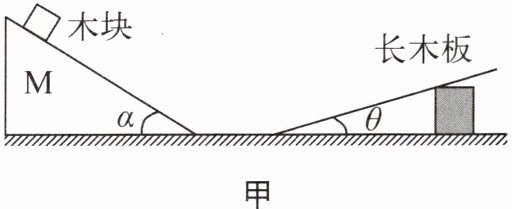
(1)他们上网查找得知:初速度相同的汽车关闭发动机后在路面滑行时,路面越粗糙,汽车滑行的距离越短。由此他们认为猜想一是
(2)为了验证猜想二,小明在老师的帮助下一起设计了如图甲所示的装置。实验时将质量不同的小木块从斜面M的同一高度自由滑下,就可以使木块以
小华设计了如图乙所示的装置进行实验,他认为只要让不同质量的小木块分别将同一弹簧压缩到相同程度后自由释放,也可以验证猜想二。老师告诉小华这一设计方案是不可行的,理由是
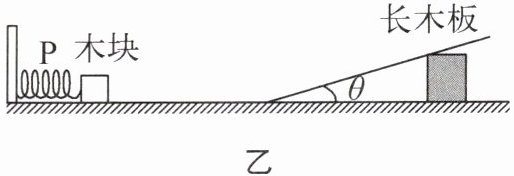
(3)他们保持长木板的粗糙程度和木块的初速度相同,分别改变木块的质量m和长木板的倾角θ,测得木块冲上长木板后运动的最大距离x,实验数据如表。分析数据可知:
①最大距离x与质量m
②最大距离x随长木板倾角θ变化的关系:θ角增大时,
|m/kg|1.2| |1.0| |0.5| | |0.3| |
|θ/°|10|20|30|30|40|45|45|50|55|55|60|65|
|x/m|1.76|1.57|1.45|1.45|1.38|1.37|1.37|1.36|1.37|1.37|1.39|1.42|
猜想一:可能与斜坡的粗糙程度有关;
猜想二:可能与物体的质量大小有关;
猜想三:可能与斜坡的倾角大小有关。
他们将与水平面平滑连接的长木板以角度θ(可改变)倾斜固定,并找来质量不同的小木块若干、光滑的斜面M(物块在斜面M上滑动时可忽略物块所受的摩擦力)和轻弹簧P等实验器材进行探究。

(1)他们上网查找得知:初速度相同的汽车关闭发动机后在路面滑行时,路面越粗糙,汽车滑行的距离越短。由此他们认为猜想一是
正确
的。(2)为了验证猜想二,小明在老师的帮助下一起设计了如图甲所示的装置。实验时将质量不同的小木块从斜面M的同一高度自由滑下,就可以使木块以
相同
的初始速度滑上长木板,通过比较木块冲上长木板的最大距离
就可以验证猜想二。小华设计了如图乙所示的装置进行实验,他认为只要让不同质量的小木块分别将同一弹簧压缩到相同程度后自由释放,也可以验证猜想二。老师告诉小华这一设计方案是不可行的,理由是
无法控制木块初速度相等
。
(3)他们保持长木板的粗糙程度和木块的初速度相同,分别改变木块的质量m和长木板的倾角θ,测得木块冲上长木板后运动的最大距离x,实验数据如表。分析数据可知:
①最大距离x与质量m
无关
(填“有关”或“无关”);②最大距离x随长木板倾角θ变化的关系:θ角增大时,
最大距离x先减小后增大
。|m/kg|1.2| |1.0| |0.5| | |0.3| |
|θ/°|10|20|30|30|40|45|45|50|55|55|60|65|
|x/m|1.76|1.57|1.45|1.45|1.38|1.37|1.37|1.36|1.37|1.37|1.39|1.42|

答案:
(1)正确 (2)相同 最大距离 无法控制木块初速度相等 (3)①无关 ②最大距离x随木块的质量减小先减小后增大 提示:
(1)路面越粗糙汽车滑行距离越短,说明最大距离与粗糙程度有关,故猜想一正确。
(2)验证猜想二时,应当控制斜面倾角、释放位置相同,只改变质量,比较木块冲上长木板的最大距离;图乙中,因同一弹簧压缩到相同程度后弹性势能相等,弹出的木块的动能也相等,则质量大的木块速度小,无法控制木块初速度相等。
(3)分析30°时质量为1.2 kg、1.0 kg,45°时质量为1.0 kg、0.5 kg,55°时质量为0.5 kg、0.3 kg的最大距离,发现这几组的最大距离相等,说明最大距离与质量无关;由表可知,当倾角θ变大时,最大距离随着木块质量的减小先减小后增大。
(1)路面越粗糙汽车滑行距离越短,说明最大距离与粗糙程度有关,故猜想一正确。
(2)验证猜想二时,应当控制斜面倾角、释放位置相同,只改变质量,比较木块冲上长木板的最大距离;图乙中,因同一弹簧压缩到相同程度后弹性势能相等,弹出的木块的动能也相等,则质量大的木块速度小,无法控制木块初速度相等。
(3)分析30°时质量为1.2 kg、1.0 kg,45°时质量为1.0 kg、0.5 kg,55°时质量为0.5 kg、0.3 kg的最大距离,发现这几组的最大距离相等,说明最大距离与质量无关;由表可知,当倾角θ变大时,最大距离随着木块质量的减小先减小后增大。
9. 在“探究电流与电阻的关系”实验中,有以下器材:电源(电压恒为4.5 V)、电压表、电流表、滑动变阻器(铭牌上标有“20 Ω 2 A”字样)和开关各一个,5 Ω、10 Ω、15 Ω、20 Ω的定值电阻各一个,导线若干。如图所示,是小林连接好的电路。
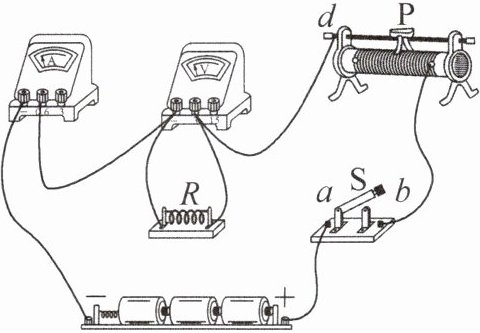
(1)实验中,小林把5 Ω的定值电阻接入电路中,此时电流表的示数为0.4 A;接着实验,他断开开关,把5 Ω的定值电阻换成10 Ω,仍然使电压表保持之前的电压值不变,则电流表的示数为
(2)在实验过程中,当他把15 Ω的定值电阻换成20 Ω后,发现把滑片P滑到最左端,电压表的示数也不能减小到想要的数值,这样就不能完成实验了。根据所学的物理知识,他想到了两个解决的办法,请你帮他完成:
方法一:把现有的滑动变阻器换成一个最大阻值至少为
方法二:其他器材不变,在电路中再串联一个定值电阻R₀,重新做实验,仍然使电压表保持原来的电压值不变,依次换用5 Ω到20 Ω这四个电阻,就能顺利完成实验了,但是R₀的阻值大小是有要求的,R₀的最大阻值为

(1)实验中,小林把5 Ω的定值电阻接入电路中,此时电流表的示数为0.4 A;接着实验,他断开开关,把5 Ω的定值电阻换成10 Ω,仍然使电压表保持之前的电压值不变,则电流表的示数为
0.2
A。(2)在实验过程中,当他把15 Ω的定值电阻换成20 Ω后,发现把滑片P滑到最左端,电压表的示数也不能减小到想要的数值,这样就不能完成实验了。根据所学的物理知识,他想到了两个解决的办法,请你帮他完成:
方法一:把现有的滑动变阻器换成一个最大阻值至少为
25
Ω的滑动变阻器;方法二:其他器材不变,在电路中再串联一个定值电阻R₀,重新做实验,仍然使电压表保持原来的电压值不变,依次换用5 Ω到20 Ω这四个电阻,就能顺利完成实验了,但是R₀的阻值大小是有要求的,R₀的最大阻值为
6.25
Ω。
答案:
(1)0.2 (2)25 6.25 提示:
(1)$ U_{V}=I_{1}R_{1}=0.4\ \text{A}×5\ \Omega=2\ \text{V} $,把$ R_{定} $由5 Ω换成10 Ω时,保持电压表示数不变,则$ I_{2}=\frac{U_{V}}{R_{2}}=\frac{2\ \text{V}}{10\ \Omega}=0.2\ \text{A} $。
(2)将$ R_{定} $换成20 Ω后,$ U_{变}=U-U_{V}=4.5\ \text{V}-2\ \text{V}=2.5\ \text{V} $,因$ \frac{U_{变}}{U_{V}}=\frac{R_{变}}{R_{定}} $,即$ \frac{2.5\ \text{V}}{2\ \text{V}}=\frac{R_{变}}{20\ \Omega} $,解得$ R_{变}=25\ \Omega $;若$ R_{变} $最大为20 Ω,至少应串联电阻$ R_{串小}=25\ \Omega-20\ \Omega=5\ \Omega $,当$ R_{定}=5\ \Omega $时,$ R_{0} $最大,$ U_{0}=U-U_{V}=4.5\ \text{V}-2\ \text{V}=2.5\ \text{V} $,$ R_{0大}=\frac{U_{0}}{I}=\frac{2.5\ \text{V}}{0.4\ \text{A}}=6.25\ \Omega $。
(1)$ U_{V}=I_{1}R_{1}=0.4\ \text{A}×5\ \Omega=2\ \text{V} $,把$ R_{定} $由5 Ω换成10 Ω时,保持电压表示数不变,则$ I_{2}=\frac{U_{V}}{R_{2}}=\frac{2\ \text{V}}{10\ \Omega}=0.2\ \text{A} $。
(2)将$ R_{定} $换成20 Ω后,$ U_{变}=U-U_{V}=4.5\ \text{V}-2\ \text{V}=2.5\ \text{V} $,因$ \frac{U_{变}}{U_{V}}=\frac{R_{变}}{R_{定}} $,即$ \frac{2.5\ \text{V}}{2\ \text{V}}=\frac{R_{变}}{20\ \Omega} $,解得$ R_{变}=25\ \Omega $;若$ R_{变} $最大为20 Ω,至少应串联电阻$ R_{串小}=25\ \Omega-20\ \Omega=5\ \Omega $,当$ R_{定}=5\ \Omega $时,$ R_{0} $最大,$ U_{0}=U-U_{V}=4.5\ \text{V}-2\ \text{V}=2.5\ \text{V} $,$ R_{0大}=\frac{U_{0}}{I}=\frac{2.5\ \text{V}}{0.4\ \text{A}}=6.25\ \Omega $。
查看更多完整答案,请扫码查看


