《2025年小题狂做九年级物理上册苏科版巅峰版》

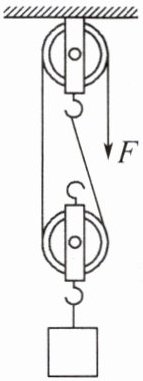
1. (2024·苏州姑苏月考)使用如图所示的滑轮组匀速提升重力不同的物体时,除了动滑轮的重力导致的额外功外,其他因素导致的额外功与总功之比为一定值。已知动滑轮的重力为4.0 N,绳子能够承受的最大拉力为50 N。当匀速提升重为15 N的物体时,滑轮组的机械效率为75%,则使用该滑轮组匀速提升物体时的机械效率的最大值为 (B)

A.92%
B.91%
C.90%
D.89%

答案： B 提示:设提升物体的高度为$h,W_{有用}=Gh=15N×h,W_{总}=\frac {W_{有用}}{η}=\frac {15N×h}{75\% }=20N×h,W_{额动}=G_{动}h=4.0N×h,W_{额其他}=W_{总}-W_{有用}-W_{额动}=20N×h-15N×h-4.0N×h=1N×h,\frac {W_{额其他}}{W_{总}}=\frac {1N×h}{20N×h}=\frac {1}{20};W_{总大}=F_{大}s=50N×2h=100N×h,W_{额其他大}=\frac {1}{20}W_{总大}=\frac {1}{20}×100N×h=5N×h,W_{有大}=W_{总大}-W_{额动}-W_{额其他大}=100N×h-4.0N×h-5N×h=91N×h,η_{大}=\frac {W_{有大}}{W_{总大}}×100\% =\frac {91N×h}{100N×h}×100\% =91\% 。$

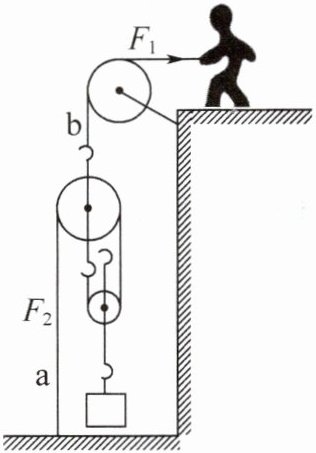
2. 小叶同学用如图所示的滑轮组提升重物,不计绳重和机械之间的摩擦,每个滑轮的重力均为10 N,与地面固定的细绳a的拉力$F_2= 105 N,$他通过细绳b用$F_1$的拉力将重物匀速提升1.5 m,所用时间为10 s。下列说法正确的是 (C)

A.物体的重力为210 N
B.细绳b的拉力为315 N
C.拉力$F_1$做功的功率为32.5 W
D.该滑轮组在使用过程中的机械效率为80%

答案： C 提示:不计绳重和摩擦时,G=2F_{2}-G_{动}=2×105N-10N=200N;以中间的动滑轮为研究对象,F_{1}=3F_{2}+G_{动}=3×105N+10N=325N;s_{a}=2h=3m,中间的滑轮受到3段绳子向下的拉力,F_{1}作用在该滑轮的挂钩上,此时费力但省距离,绳子b移动的距离$s_{b}=1m,W_{总}=F_{1}s_{b}=325N×1m=325J,P=\frac {W_{总}}{t}=\frac {325J}{10s}=32.5W,W_{有用}=Gh=200N×1.5m=300J,η=\frac {W_{有用}}{W_{总}}×100\% =\frac {300J}{325J}×100\% \approx 92.3\% 。$

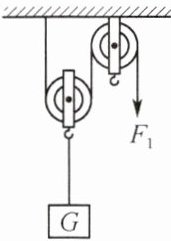
3. 小李同学利用如图所示的滑轮组匀速提升重物。第一次提升的重物A的重力为Gₐ,加在绳子自由端的拉力为$F_1,$重物上升的速度为$v_1,$运动时间为$t_1。$第二次提升的重物B的重力为Gᵦ,加在绳子自由端的拉力为$F_2,$重物上升的速度为$v_2,$运动时间为$t_2。$已知$F_1:Gₐ= 5:8,Gᵦ:Gₐ= 3:2,v_1:v_2= 2:1,t_1:t_2= 2:3。$动滑轮的重力不能忽略,不计绳重与摩擦的影响。下列对两个过程的分析错误的是 ( C )


A.拉力之比为$F_1:F_2= 5:7$
B.拉力的功率之比为$P_1:P_2= 10:7$
C.机械效率之比为$η_1:η_2= 7:8$
D.额外功之比为$W_1:W_2= 4:3$

答案： C 提示:已知$F_{1}:G_{A}=5:8,G_{B}:G_{A}=3:2$,假设$G_{A}=8F$,则$G_{B}=12F,F_{1}=5F$,图中使用的滑轮组,$n=2$,不计绳重与摩擦的影响,拉力$F_{1}=\frac {1}{2}(G_{A}+G_{动})$,则动滑轮重$G_{动}=2F_{1}-G_{A}=2×5F-8F=2F$,拉力$F_{2}=\frac {1}{2}(G_{B}+G_{动})=\frac {1}{2}×(12F+2F)=7F$,所以$F_{1}:F_{2}=5:7$;拉力的功率之比$P_{1}:P_{2}=F_{1}v_{1}:F_{2}v_{2}=(5F×2):(7F×1)=10:7$;不计绳重与摩擦的影响,滑轮组的机械效率$η_{甲}=\frac {W_{有用}}{W_{总}}×100\% =\frac {W_{有用}}{W_{有用}+W_{额外}}×100\% =\frac {Gh}{Gh+G_{动}h}×100\% =\frac {G}{G+G_{动}}×100\% $,则$η_{1}:η_{2}=\frac {G_{A}}{G_{A}+G_{动}}:\frac {G_{B}}{G_{B}+G_{动}}=\frac {8}{8+2}:\frac {12}{12+2}=14:15$;不计绳重与摩擦的影响,额外功$W_{额外}=G_{动}h,h_{1}:h_{2}=v_{1}t_{1}:v_{2}t_{2}=(2×2):(1×3)=4:3$,额外功$W_{1}:W_{2}=G_{动}h_{1}:G_{动}h_{2}=h_{1}:h_{2}=4:3$。

4. (2024·镇江句容模拟)如图所示,小型牵引车通过滑轮组匀速打捞起深井中的均质物体,物体上升的速度保持1 m/s不变,已知物体重$1.2×10^3N,$密度为$1.6×10^3kg/m^3。$测得物体在出水面前、后牵引车作用在绳子上的拉力之比为1:2,若不计摩擦、绳重及水的阻力,g取10 N/kg,下列结果错误的是 (A)
A.物体出水面前牵引车拉力的功率为500 W
B.物体浸没在水中受到的浮力为750 N
C.物体出水面前牵引车的拉力为250 N
D.物体出水面前滑轮组的效率是60%

答案： A 提示:物体出水面前,$V_{排}=V_{物}=\frac {G_{物}}{ρ_{物}g}=\frac {1.2×10^{3}N}{1.6×10^{3}kg/m^{3}×10N/kg}=0.075m^{3},F_{浮}=ρ_{水}gV_{排}=1×10^{3}kg/m^{3}×10N/kg×0.075m^{3}=750N$;不计摩擦、绳重及水的阻力,$F_{1}=\frac {1}{3}(G_{物}+G_{动}-F_{浮})=\frac {1}{3}×(1.2×10^{3}N+G_{动}-750N)$,物体出水面后,$F_{2}=\frac {1}{3}(G_{物}+G_{动})=\frac {1}{3}×(1.2×10^{3}N+G_{动})$,因$F_{1}:F_{2}=1:2$,解得$G_{动}=300N,F_{1}=250N,F_{2}=500N;v_{F}=3v_{物}=3×1m/s=3m/s,P_{1}=F_{1}v_{F}=250N×3m/s=750W;η=\frac {W_{有用}}{W_{总}}×100\% =\frac {(G_{物}-F_{浮})h}{F_{1}s}×100\% =\frac {G_{物}-F_{浮}}{3F_{1}}×100\% =\frac {1.2×10^{3}N-750N}{3×250N}×100\% =60\% $。

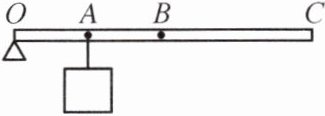
5. 如图所示,一根均匀的细木棒OC,OA= 1/4OC,B为OC的中点。在C点用始终竖直向上50 N的拉力将挂在A点的重为180 N的物体匀速提升0.1 m。提升该物体做的有用功是18J,总功是20J,木棒的机械效率为90%,木棒重为10N(不计一切摩擦)。如果将拉力从C点移动至B点,则机械效率会不变(填“增大”“不变”或“减小”)。

答案： 18 20 90% 10 不变 提示:$W_{有用}=Gh=180N×0.1m=18J$;因$OA=\frac {1}{4}OC,s=4h=4×0.1m=0.4m,W_{总}=Fs=50N×0.4m=20J;η=\frac {W_{有用}}{W_{总}}×100\% =\frac {18J}{20J}×100\% =90\% ;W_{额外}=W_{总}-W_{有用}=20J-18J=2J$,B为OC的中点,故$OB=2OA$,物体上升0.1m时,B点(重心)上升$h'=0.2m$,不计摩擦和绳重,$G_{杆}=\frac {W_{额外}}{h'}=\frac {2J}{0.2m}=10N$;拉力从C点移至B点,两次物体被提升的高度相同,$W_{有用}$相同,杠杆被提升的高度也相同,$W_{额外}$也相同,由$η=\frac {W_{有用}}{W_{总}}×100\% =\frac {W_{有用}}{W_{有用}+W_{额外}}×100\% $可知,机械效率不变。