第111页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
1.(2024·盐城大丰月考)如图甲所示,某健身俱乐部通过压力传感器获取运动者的运动数据,其工作原理如图乙所示。电源电压不变,$R_{1}$为定值电阻,压力传感器$R$的阻值随压力的增加而减小。在人从与蹦床接触至下落到最低点的过程中,下列说法中正确的是(
A.运动员在此过程中,动能增大,重力势能减小,机械能不变
B.电流表的示数逐渐变大
C.电压表的示数逐渐变小
D.电压表与电流表的比值逐渐变大
B
)A.运动员在此过程中,动能增大,重力势能减小,机械能不变
B.电流表的示数逐渐变大
C.电压表的示数逐渐变小
D.电压表与电流表的比值逐渐变大
答案:
B 提示:人从与蹦床接触至下落到最低点的过程中,速度先变大后变小,动能先变大后变小,重力势能减小,机械能不守恒;R上受到的压力增加,阻值减小,$U_R$变小,V表示数变大,电流变大;V表与A表的示数的比值即$R_1$的阻值,其比值不变。
2.(2024·常州金坛模拟)如图甲所示是脚踏式翻盖垃圾桶的实物图,翻盖的原理是由两个杠杆$AO_{1}B及DCO_{2}$组合而成,图乙是两个杠杆组合的示意图。桶盖的质量为400 g,桶盖的直径为60 cm。脚踏杆和其他连接杆的质量不计,已知$AO_{1}= 24\ \text{cm}$,$O_{1}B= 18\ \text{cm}$,$CO_{2}= 5\ \text{cm}$,桶盖$DC$质量分布均匀,厚度不计,桶盖闭合时,连接杆$BC$处于竖直状态,$g取10\ \text{N/kg}$。下列说法正确的是(
D
)
答案:
D 提示:因$AO_1>O_1B$,即$L_1>L_2$,故$AO_1B$为省力杠杆;因$CO_2<DO_2$,即$L_1<L_2$,故$DCO_2$为费力杠杆;将桶盖翻开$30^\circ$时,桶盖重心上升高度$h=0.5×35\ \text{cm}=17.5\ \text{cm}=0.175\ \text{m}$,克服桶盖重力做功$W=Gh=mgh=0.4\ \text{kg}×10\ \text{N/kg}×0.175\ \text{m}=0.7\ \text{J}$;设脚对A点的作用力为F,顶杆对B点的作用力为$F_1$,顶杆对桶盖上C点的作用力为$F_2$,有$F× AO_1=F_1× O_1B$,$G× DO_2=F_2× CO_2$,$F_1=F_2$,$G=mg=0.4\ \text{kg}×10\ \text{N/kg}=4\ \text{N}$,$DO_2=30\ \text{cm}+5\ \text{cm}=35\ \text{cm}$,解得$F=\frac{O_1B× DO_2}{CO_2× AO_1}× G=\frac{18\ \text{cm}×35\ \text{cm}}{5\ \text{cm}×24\ \text{cm}}×4\ \text{N}=21\ \text{N}$。
3.(2024·无锡宜兴期中)如图甲所示,水平放置的方形容器里有一个重为8 N、棱长为10 cm的正方体物块M,M与容器底部不密合。以5 mL/s的恒定水流向容器内注水,容器中水的深度$h随时间t$的变化关系如图乙所示,下列选项正确的是( )
 A. 当$t= 140\ \text{s}$时,物块M在水中处于悬浮状态
A. 当$t= 140\ \text{s}$时,物块M在水中处于悬浮状态
B. 当$t= 140\ \text{s}$时,水对容器底部的压力大小是15 N
C. 图乙中$a$的值是9
D. 40~140 s时段,浮力对物块M做的功是0.3 J
B
 A. 当$t= 140\ \text{s}$时,物块M在水中处于悬浮状态
A. 当$t= 140\ \text{s}$时,物块M在水中处于悬浮状态B. 当$t= 140\ \text{s}$时,水对容器底部的压力大小是15 N
C. 图乙中$a$的值是9
D. 40~140 s时段,浮力对物块M做的功是0.3 J
答案:
B 提示:$\rho_M=\frac{G}{gV}=\frac{8\ \text{N}}{10\ \text{N/kg}×0.001\ \text{m}^3}=0.8×10^3\ \text{kg/m}^3<\rho_水$,当$t=140\ \text{s}$时,水深$h=12\ \text{cm}>L_M$,物块M在水中漂浮;当$t=140\ \text{s}$时,$V_水=vt=5\ \text{mL/s}×140\ \text{s}=700\ \text{mL}=7×10^{-4}\ \text{m}^3$,$G_水=\rho_水gV_水=1×10^3\ \text{kg/m}^3×10\ \text{N/kg}×7×10^{-4}\ \text{m}^3=7\ \text{N}$,水对底部压力$F=G_水+G_M=7\ \text{N}+8\ \text{N}=15\ \text{N}$;当$t=40\ \text{s}$时,物块M刚开始漂浮,$F_浮=G_M=8\ \text{N}$,$V_排=\frac{F_浮}{\rho_水g}=\frac{8\ \text{N}}{1×10^3\ \text{kg/m}^3×10\ \text{N/kg}}=8×10^{-4}\ \text{m}^3=800\ \text{cm}^3$,物块M浸入水中的深度$a=\frac{V_排}{S_M}=\frac{800\ \text{cm}^3}{(10\ \text{cm})^2}=8\ \text{cm}$;在$40~140\ \text{s}$内,物块M上升的高度$h'=12\ \text{cm}-8\ \text{cm}=4\ \text{cm}=0.04\ \text{m}$,$W=F_浮h'=8\ \text{N}×0.04\ \text{m}=0.32\ \text{J}$。
4.(2024·南通海门期中)跨学科实践小组设计了如图甲所示的电路来监测“智能种植园”内的温度变化,其中的“恒流源”是一个特殊电源,电流大小由电源内部结构决定,当电阻$R$变化时,通过$R$的电流大小保持不变。电阻$R$的阻值随温度的变化规律如图乙所示,通过数字电压表的示数可反映环境的温度。某次环境温度从$15^{\circ}\text{C}上升到25^{\circ}\text{C}$,电压表的示数变化了0.2 V。下列说法正确的是(
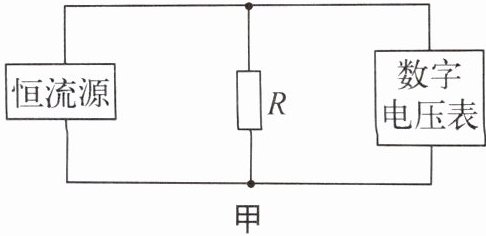
A.每升高$1^{\circ}\text{C}$,$R$的阻值增大0.5 Ω

B.此时电路中通过$R$的电流为2 mA
C.环境温度为$20^{\circ}\text{C}$时,电压表的示数为2.3 V
D.增大恒流源电流值可增大该装置的灵敏度
D
)
A.每升高$1^{\circ}\text{C}$,$R$的阻值增大0.5 Ω

B.此时电路中通过$R$的电流为2 mA
C.环境温度为$20^{\circ}\text{C}$时,电压表的示数为2.3 V
D.增大恒流源电流值可增大该装置的灵敏度
答案:
D 提示:温度上升$80^\circ\text{C}$时,电阻增大$80\ \Omega$,故每升高$1^\circ\text{C}$,$R$增大$1\ \Omega$;从$15^\circ\text{C}$上升到$25^\circ\text{C}$,电阻增加量为$1×10\ \Omega=10\ \Omega$,恒定电流$I=\frac{\Delta U}{\Delta R}=\frac{0.2\ \text{V}}{10\ \Omega}=0.02\ \text{A}=20\ \text{mA}$;温度变为$20^\circ\text{C}$时,$R=120\ \Omega$,$U=IR=0.02\ \text{A}×120\ \Omega=2.4\ \text{V}$;为了增大装置的灵敏度,应在温度变化量相同时,变化更大的电压,故应换一个电流更大的恒流源。
查看更多完整答案,请扫码查看


