《2025年小题狂做九年级物理上册苏科版巅峰版》

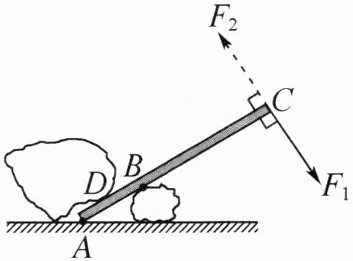
9. 如图所示是用木棒撬石块的示意图。撬石块有两种方法:第一种是以B点为支点,在C点用与木棒垂直的力$F_1$向下撬;第二种是以A点为支点,在C点用与木棒垂直的力$F_2$向上撬(木棒自重不计)。已知AC= 2m,BC= 1.6m,且AD= DB。则:

(1) 若石块对木棒的阻力f为100N,求垂直于木棒向上用力时的动力$F_2$的大小。
(2) 假设石块对木棒的阻力始终为f,采用两种不同方向用力时,动力$F_1与F_2$的差值为30N,求阻力f的大小。

答案：
(1)10N
(2)1200N 提示:
(1)垂直于木棒向上用力时,支点为A,动力臂$l_1=AC=2m,$阻力臂$l_2=AD=(AC-BC)/2=(2m-1.6m)/2=0.2m,$由$F_2×l_1=f×l_2,$解得$F_2=(f×l_2)/l_1=(100N×0.2m)/2m=10N。$
(2)垂直于木棒向下用力时,支点为B,动力臂$l_1^'=BC=1.6m,$阻力臂$l_2^'=BD=(AC-BC)/2=(2m-1.6m)/2=0.2m,$由$F_1×l_1^'=f×l_2^'$得$F_1=(f×l_2^')/l_1^',$则有$(f×l_2^')/l_1^'-(f×l_2)/l_1=30N,$即(f×0.2m)/1.6m-(f×0.2m)/2m=30N,解得f=1200N。

10. 如图甲是一种壶口处配有自动开合小壶盖的电水壶。图乙是自动开合小壶盖的简化侧视图,OA是小壶盖,C是其重力作用点,B是小壶盖的配重,OB是配重柄,AOB能绕固定点O自由转动。

(1) 请在图乙中作出小壶盖的重力G及其力臂l。
(2) 已知:小壶盖质量为4g,OA= 3cm,OC= 1.4cm,OB= 1cm,∠AOB= 135°。要求倒水时,壶身最多倾斜45°,小壶盖便自动打开;壶身竖直时,小壶盖在水平位置自动闭合。求配重B的质量取值范围。(配重柄质量和O点的摩擦均忽略不计,取√2= 1.4)

答案：

(1)如图甲所示
(2)4～7.89g 提示:
(2)①当配重柄水平时,杠杆示意图如图乙所示，此时配重的力臂最大、小壶盖重力的力臂最小,即配重的质量最小,OD和OC间的夹角为45°,OD=
(1)/√2×OC=
(1)/√2×1.4cm=1cm,因$G_1l_1=G_2l_2,$即$m_1g×OD=m_2g×OB,$则$m_2=(m_1×OD)/OB=(4g×1cm)/1cm=4g;②$当壶盖水平时,杠杆的示意图如图丙所示,此时配重的力臂最小、壶盖重力的力臂最大,即配重的质量最大,OE和OB间的夹角为45°,OE=
(1)/√2×OB=
(1)/√2×1cm≈0.71cm,因$G_1l_1^'=G_2^'l_2^',$即$m_1g×OC=m_2^'g×OE,$则$m_2^'=(m_1×OC)/OE=(4g×1.4cm)/0.71cm≈7.89g,$故配重B的质量范围为4～7.89g。
　，
　　　　
　　　　　　　　　　乙
　　　

11. 如图所示的装置中,轻质杠杆的支点为O,物块A、B通过轻质细线悬挂于Q点,当柱形薄壁容器中没有水时,物块C悬挂于E点,杠杆在水平位置平衡。当往容器中加入质量为m的水时(水还未浸没物块B),为使杠杆在水平位置平衡,物块C应悬挂于F点,A、B为均匀实心正方体,A、B的边长均为20cm。B的下表面到容器底的距离为20cm,柱形容器的底面积为$S= 600cm^2。$G_A= 1.6N,G_B= 12.8N,OQ= 4cm,OE= 14.4cm,OF= 10.4cm。ρ_水$=1.0×10^3kg/m^3,$杠杆重力对平衡的影响忽略不计,细线重力忽略不计,物块不吸水。求:(g取10N/kg)

(1) 物块C的重力。
(2) 物块C悬挂于F点时,物块B受到的浮力。
(3) 物块B浸入水中的深度h_浸。
(4) 往容器中加入水的质量m。

答案：
(1)4N
(2)4N
(3)1cm
(4)12.2kg 提示:
(1)Q点为阻力作用点$,F_2=G_A+G_B=1.6N+12.8N=14.4N,OQ$为阻力臂,OE为动力臂,杠杆在水平位置平衡时,有$F_2×L_OQ=G_C×L_OE,G_C=(F_2×L_OQ)/L_OE=(14.4N×4cm)/14.4cm=4N。$
(2)物块C悬挂于F点时,有$F_2^'×L_OQ=G_C×L_OF,F_2^'=(G_C×L_OF)/L_OQ=(4N×10.4cm)/4cm=10.4N,F_$浮$B=G_A+G_B-F_2^'=1.6N+12.8N-10.4N=4N。$
(3)V_排B=F_浮B/(ρ_水$g)=4N/(1.0×10^3kg/m^3×10N/kg)=4×10^(-4)m^3=400cm^3,$物块B浸入水中的深度h_浸=V_排$B/S_B=400cm^3/(20cm×20cm)=1cm。$
(4)容器中水深h=h^'+h_浸=20cm+1cm=21cm,V_水=S_容h-V_排$B=600cm^2×21cm-400cm^3=12200cm^3=1.22×10^(-2)m^3,m_$水=ρ_水V_水$=1.0×10^3kg/m^3×1.22×10^(-2)m^3=12.2kg。$