《2025年小题狂做九年级物理上册苏科版巅峰版》

11. 如图所示是一个自制密度秤,其外形与杆秤类似。装秤钩的B处吊着一个体积为50$cm^{3}$、密度为6$g/cm^{3}$的均匀合金块,提纽位于O处,质量为100 g的秤砣放在A处时,秤杆恰好水平平衡(图甲)。把合金块浸没在待测密度的液体中时,移动秤砣便可直接在杆上读出液体的密度。

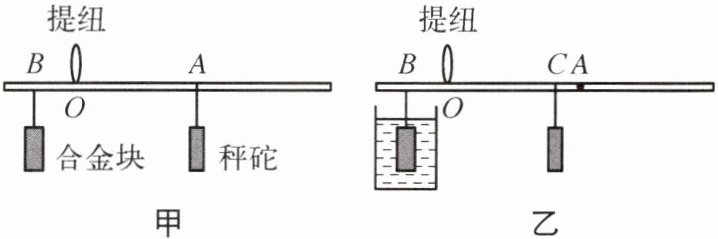
(1)在图甲位置平衡时,整个装置的重心位于O处(填“A处”“O处”或“AO之间的某一位置”)。
(2)当测量水的密度时,将合金块浸没在水中,秤砣移到C处时密度秤水平平衡,如图乙所示,现在向水中加入一定量的食盐,则秤砣向左(填“左”或“右”)移才能使密度秤再次在水平位置平衡。
(3)若测量液体的密度时,合金块没有完全浸没,则测量值小于(填“大于”“等于”或“小于”)真实值。
(4)若测量液体的密度时,合金块没有完全浸没,则测量值1.2×10³kg/m³或0.8×10³kg/m³。

答案：
(1)O处
(2)左
(3)小于
(4)1.2×10³kg/m³或0.8×10³kg/m³ 提示:
(2)V排不变时,ρ液变大,F浮也变大,B处的拉力变小;提纽左侧动力减小,提纽右侧阻力臂应减小,故秤砣应向左移。
(3)如动力臂不变,未完全浸没在液体中时,提纽左侧动力比完全浸没时的大,阻力臂应变大,秤砣向右移,测量值小于真实值。
(4)m合金 = ρ合金V合金 = 6g/cm³×50cm³ = 300g = 0.3kg,G合金 = m合金g = 0.3kg×10N/kg = 3N,G秤砣 = 0.1kg×10N/kg = 1N,金属块浸没水中时,F浮 = ρ水gV排 = 1.0×10³kg/m³×10N/kg×50×10⁻⁶m³ = 0.5N。杠杆平衡时,有(G合金 - F浮)×OB = G秤砣×OC,(3N - 0.5N)×20cm = 1N×OC,解得OC = 50cm,则OD = 48cm或OD = 52cm。当OD = 48cm时,(G合金 - F浮')×OB = G秤砣×OD,(3N - F浮')×20cm = 1N×48cm,解得F浮' = 0.6N,ρ液' = F浮'/gV排 = 0.6N/(10N/kg×50×10⁻⁶m³)=1.2×10³kg/m³;当OD = 52cm时,(G合金 - F浮'')×OB = G秤砣×OD,(3N - F浮'')×20cm = 1N×52cm,解得F浮'' = 0.4N,ρ液'' = F浮''/gV排 = 0.4N/(10N/kg×50×10⁻⁶m³)=0.8×10³kg/m³。

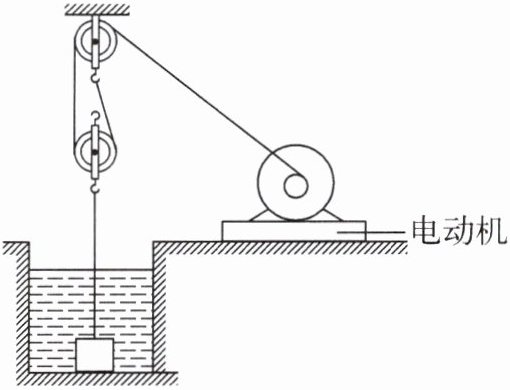
12. 小超与同学到某工地参观,看到工人操作电动机,通过如图所示的滑轮组将正方体石料从水池底竖直匀速吊起。他们通过调查得知：石料的边长为0.2 m,密度为$2.5×10^{3}kg/m^{3}$,石料上升时的速度恒为0.4 m/s,圆柱形水池的底面积为0.2$m^{2}$,动滑轮重为30 N。请根据他们的调查数据,求：(不计绳重和摩擦,$\rho_{水}= 1.0×10^{3}kg/m^{3}$,g取10 N/kg)
(1)石料露出水面前受到的浮力。
(2)石料的重力。
(3)石料露出水面前滑轮组的机械效率。
(4)石料从刚露出水面到完全露出水面所用的时间,并推导出该过程中电动机的输出功率P(单位：W)与时间t(单位：s)的函数关系式。

答案：
(1)80N
(2)200N
(3)80%
(4)0.4s P = 80t + 60(W),0≤t≤0.4s 提示:
(1)F浮 = ρ水gV排 = 1.0×10³kg/m³×10N/kg×(0.2m)³ = 80N。
(2)G石 = m石g = ρ石gV石 = 2.5×10³kg/m³×10N/kg×(0.2m)³ = 200N。
(3)η = W有用/W总×100% = W有用/(W有用 + W额外)×100% = (G石 - F浮)h/((G石 - F浮)h + G动h)×100% = (200N - 80N)/(120N + 30N)×100% = 80%。
(4)当石料全露出水面时,△h水 = V石/S池 = 8×10⁻³m³/0.2m² = 0.04m,石料实际上升的高度h' = L - △h水 = 0.2m - 0.04m = 0.16m,石料被拉出水面的时间t = h'/v石 = 0.16m/0.4m/s = 0.4s,设石料刚露出水面时t = 0,某一时刻上升的高度h = v石t = 0.4m/s×t = 0.4t,△h水' = V露/(S池 - S石)=v石tS石/(S池 - S石)=(0.4m/s×t×(0.2m)²)/(0.2m² - (0.2m)²)=0.1t,h露 = h + △h水' = 0.4t + 0.1t = 0.5t,V排 = (L - h露)S石 = (0.2m - 0.5t)×(0.2m)² = 8×10⁻³ - 0.02t,F浮 = ρ水gV排 = 1.0×10³kg/m³×10N/kg×(8×10⁻³ - 0.02t)= - 200t + 80(N),绳端拉力F = (G石 + G动 - F浮)/2 = (200N + 30N - (- 200t + 80)N)/2 = 100t + 75(N),P = FvF = (100t + 75)N×2×0.4m/s = 80t + 60(W),0≤t≤0.4s。