第99页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
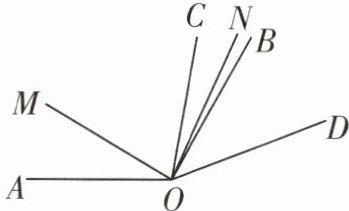
6 如图,$∠AOC= 100^{\circ }$,$∠BOD= 40^{\circ }$,射线OM在$∠AOB$内部,射线ON在$∠COD$内部,$∠AOB= 4∠AOM$,$∠COD= 4∠CON$,求$∠MON$的度数.

答案:
解:设∠AOM=x,∠CON=y,则∠AOB=4x,∠COD=4y,所以∠BOC=∠AOB - ∠AOC=∠COD - ∠BOD,即4x - 100°=4y - 40°,所以x - y=15°,所以∠MON=∠AOC+∠CON - ∠AOM=100°+y - x=100° - (x - y)=85°.
7 新趋势·过程性学习[2025太原期末]阅读与思考:下面是小钧课后思考的一部分笔记,请你认真阅读,并完成相应的任务.
线段与角的研究一致性
在第4章《几何图形初步》的学习中,我认识到“线段”和“角”在研究方法和研究路径上具有一致性,同时,我还发现,在解决线段和角的某些问题时,其方法也有许多一致性.
【问题1】如图1,①点C是线段AB上一点,②点M是线段AC的中点,点N是线段BC的中点,③若$AB= 10$,$AM= 2$,求MN的长.
分析:在审题时,我用下划线和序号①②③分别标记了题目的已知条件,并逐次分析如下:
由条件①,可得$AC+BC= AB$;将条件②得到的部分结论和条件③标记在图1中.
解答:下面是我解决问题1的过程.
因为点M是线段AC的中点,所以$AM= MC= \frac {1}{2}AC$.因为$AM= 2$,所以$MC= 2$,所以$AC= 4$.
因为点C是线段AB上一点,所以$BC= AB-AC= 10-4= 6… …$
反思1:我发现,根据题中的条件,能求出图1中所有线段的长度.若去掉任何一个条件,就无法求出所有线段了.
反思2:根据问题1的结果,可以发现MN与AB有特殊的数量关系,即$MN= $____AB.
反思3:我发现若将条件①改为“点C是直线AB上的一点”,去掉题中的条件____(选填“②”或“③”),MN与AB之间的关系也不会变化.
在练习中,我发现下面的问题2与问题1有许多一致性,分析时,我也用下划线和①②③标记了已知条件,可类比问题1的思路解答.
【问题2】如图2,$∠AOB<180^{\circ }$,将射线OB绕点O按逆时针方向旋转得到射线OC(旋转的度数小于$180^{\circ }$).已知①射线OC在$∠AOB$内部,②OM,ON分别平分$∠AOC和∠BOC$.③若$∠AOB= 120^{\circ }$,$∠AOM= 40^{\circ }$,求$∠MON$的度数.
解答:……$ $
反思4:……$ $
任务:(1)请将阅读材料中问题1的解答过程和反思2、反思3补充完整;
(2)请完成问题2的解答;
(3)请类比小钧问题1的反思,写出完成问题2后你的一条反思.
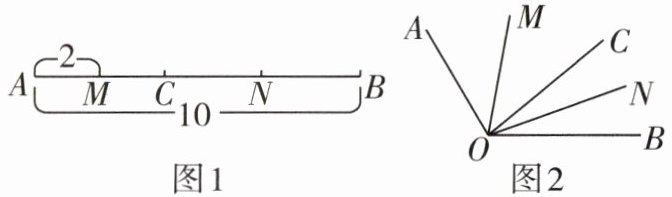
线段与角的研究一致性
在第4章《几何图形初步》的学习中,我认识到“线段”和“角”在研究方法和研究路径上具有一致性,同时,我还发现,在解决线段和角的某些问题时,其方法也有许多一致性.
【问题1】如图1,①点C是线段AB上一点,②点M是线段AC的中点,点N是线段BC的中点,③若$AB= 10$,$AM= 2$,求MN的长.
分析:在审题时,我用下划线和序号①②③分别标记了题目的已知条件,并逐次分析如下:
由条件①,可得$AC+BC= AB$;将条件②得到的部分结论和条件③标记在图1中.
解答:下面是我解决问题1的过程.
因为点M是线段AC的中点,所以$AM= MC= \frac {1}{2}AC$.因为$AM= 2$,所以$MC= 2$,所以$AC= 4$.
因为点C是线段AB上一点,所以$BC= AB-AC= 10-4= 6… …$
反思1:我发现,根据题中的条件,能求出图1中所有线段的长度.若去掉任何一个条件,就无法求出所有线段了.
反思2:根据问题1的结果,可以发现MN与AB有特殊的数量关系,即$MN= $____AB.
反思3:我发现若将条件①改为“点C是直线AB上的一点”,去掉题中的条件____(选填“②”或“③”),MN与AB之间的关系也不会变化.
在练习中,我发现下面的问题2与问题1有许多一致性,分析时,我也用下划线和①②③标记了已知条件,可类比问题1的思路解答.
【问题2】如图2,$∠AOB<180^{\circ }$,将射线OB绕点O按逆时针方向旋转得到射线OC(旋转的度数小于$180^{\circ }$).已知①射线OC在$∠AOB$内部,②OM,ON分别平分$∠AOC和∠BOC$.③若$∠AOB= 120^{\circ }$,$∠AOM= 40^{\circ }$,求$∠MON$的度数.
解答:……$ $
反思4:……$ $
任务:(1)请将阅读材料中问题1的解答过程和反思2、反思3补充完整;
(2)请完成问题2的解答;
(3)请类比小钧问题1的反思,写出完成问题2后你的一条反思.
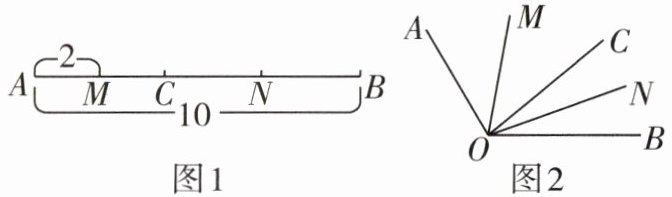
答案:
解:
(1)补充的问题1的解答过程如下:因为点N是线段BC的中点,所以CN=BN=$\frac{1}{2}$BC=3.因为MC=2,所以MN=MC+CN=2+3=5.
反思2:$\frac{1}{2}$
反思3:③ 若将条件①改为“点C是直线AB上的一点”,去掉题中的条件③,MN与AB之间的关系也不会变化,理由如下.
(ⅰ)当点C在点A,点B之间时,如图1所示,因为点M是线段AC的中点,点N是线段BC的中点,所以设AM=MC=a,CN=BN=b,所以AC=2a,BC=2b,MN=MC+CN=a+b,所以AB=AC+BC=2(a+b),所以MN=$\frac{1}{2}$AB.
(ⅱ)当点C在点A的左侧时,如图2所示,因为点M是线段AC的中点,点N是线段BC的中点,所以设AM=MC=a,CN=BN=b,所以AC=2a,所以AN=CN - AC=b - 2a,所以MN=AM+AN=a+b - 2a=b - a,AB=AN+BN=b - 2a+b=2b - 2a,所以MN=$\frac{1}{2}$AB.
(ⅲ)当点C在点B的右侧时,如图3所示,因为点M是线段AC的中点,点N是线段BC的中点,所以设AM=MC=a,CN=BN=b,所以BC=2b,所以MB=MC - BC=a - 2b,所以MN=MB+BN=a - 2b+b=a - b,AB=AM+MB=a+a - 2b=2a - 2b,所以MN=$\frac{1}{2}$AB.

(2)因为OM平分∠AOC,∠AOM=40°,所以∠COM=∠AOM=40°,所以∠AOC=∠COM+∠AOM=80°.因为∠AOB=120°,所以∠BOC=∠AOB - ∠AOC=120° - 80°=40°.因为ON平分∠BOC,所以∠CON=∠BON=$\frac{1}{2}$∠BOC=20°,所以∠MON=∠COM+∠CON=40°+20°=60°.
(3)(反思答案不唯一,合理即可)
反思1:我发现,根据题中的条件,能求出题图2中所有角的度数.若去掉任何一个条件,就无法求出所有角的度数了.
反思2:根据问题2的结果,可以发现∠MON与∠AOB之间有特殊的数量关系,即∠MON=$\frac{1}{2}$∠AOB.
反思3:我发现若条件①、条件②不动,去掉条件③,依然有∠MON=$\frac{1}{2}$∠AOB,理由如下:因为射线OC在∠AOB内部,OM,ON分别平分∠AOC和∠BOC,所以设∠COM=∠AOM=α,∠CON=∠BON=β,所以∠AOC=2α,∠BOC=2β,∠MON=∠COM+∠CON=α+β,所以∠AOB=∠AOC+∠BOC=2α+2β,所以∠MON=$\frac{1}{2}$∠AOB.
解:
(1)补充的问题1的解答过程如下:因为点N是线段BC的中点,所以CN=BN=$\frac{1}{2}$BC=3.因为MC=2,所以MN=MC+CN=2+3=5.
反思2:$\frac{1}{2}$
反思3:③ 若将条件①改为“点C是直线AB上的一点”,去掉题中的条件③,MN与AB之间的关系也不会变化,理由如下.
(ⅰ)当点C在点A,点B之间时,如图1所示,因为点M是线段AC的中点,点N是线段BC的中点,所以设AM=MC=a,CN=BN=b,所以AC=2a,BC=2b,MN=MC+CN=a+b,所以AB=AC+BC=2(a+b),所以MN=$\frac{1}{2}$AB.
(ⅱ)当点C在点A的左侧时,如图2所示,因为点M是线段AC的中点,点N是线段BC的中点,所以设AM=MC=a,CN=BN=b,所以AC=2a,所以AN=CN - AC=b - 2a,所以MN=AM+AN=a+b - 2a=b - a,AB=AN+BN=b - 2a+b=2b - 2a,所以MN=$\frac{1}{2}$AB.
(ⅲ)当点C在点B的右侧时,如图3所示,因为点M是线段AC的中点,点N是线段BC的中点,所以设AM=MC=a,CN=BN=b,所以BC=2b,所以MB=MC - BC=a - 2b,所以MN=MB+BN=a - 2b+b=a - b,AB=AM+MB=a+a - 2b=2a - 2b,所以MN=$\frac{1}{2}$AB.

(2)因为OM平分∠AOC,∠AOM=40°,所以∠COM=∠AOM=40°,所以∠AOC=∠COM+∠AOM=80°.因为∠AOB=120°,所以∠BOC=∠AOB - ∠AOC=120° - 80°=40°.因为ON平分∠BOC,所以∠CON=∠BON=$\frac{1}{2}$∠BOC=20°,所以∠MON=∠COM+∠CON=40°+20°=60°.
(3)(反思答案不唯一,合理即可)
反思1:我发现,根据题中的条件,能求出题图2中所有角的度数.若去掉任何一个条件,就无法求出所有角的度数了.
反思2:根据问题2的结果,可以发现∠MON与∠AOB之间有特殊的数量关系,即∠MON=$\frac{1}{2}$∠AOB.
反思3:我发现若条件①、条件②不动,去掉条件③,依然有∠MON=$\frac{1}{2}$∠AOB,理由如下:因为射线OC在∠AOB内部,OM,ON分别平分∠AOC和∠BOC,所以设∠COM=∠AOM=α,∠CON=∠BON=β,所以∠AOC=2α,∠BOC=2β,∠MON=∠COM+∠CON=α+β,所以∠AOB=∠AOC+∠BOC=2α+2β,所以∠MON=$\frac{1}{2}$∠AOB.
查看更多完整答案,请扫码查看


