《2025年一遍过七年级数学上册沪科版》

1 [2023 宜宾中考]下列计算正确的是( )

A.$4a - 2a = 2$
B.$2ab + 3ba = 5ab$
C.$a + a^{2}= a^{3}$
D.$5x^{2}y - 3xy^{2}= 2xy$

答案： B

2 [2024 云南中考]按一定规律排列的代数式：$2x$,$3x^{2}$,$4x^{3}$,$5x^{4}$,$6x^{5}$,…,第 $n$ 个代数式是( )

A.$2x^{n}$
B.$(n - 1)x^{n}$
C.$nx^{n + 1}$
D.$(n + 1)x^{n}$

答案： D

3 新趋势·代数推理 [2023 宜昌中考]在月历上,某些数满足一定的规律。如图是某年 $8$ 月份的月历,任意选择其中所示的含 $4$ 个数的方框部分,设右上角的数为 $a$,则下列叙述中正确的是( )


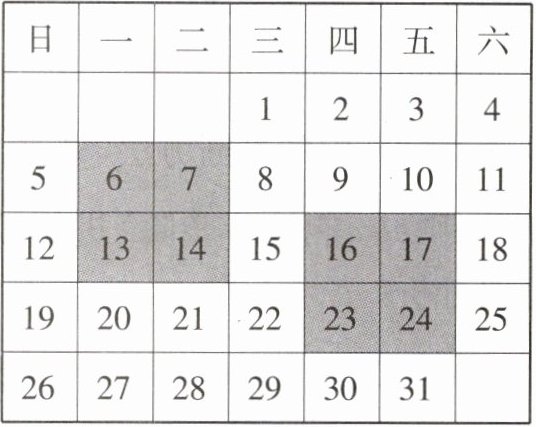
A.左上角的数为 $a + 1$
B.左下角的数为 $a + 7$
C.右下角的数为 $a + 8$
D.方框中 $4$ 个位置的数相加,结果是 $4$ 的倍数

答案： D

4 [2023 德阳中考]在“点燃我的梦想,数学皆有可能”数学创新设计活动中,“智多星”小强设计了一个数学探究活动。对依次排列的两个整式 $m$,$n$ 按如下规律进行操作：第 $1$ 次操作后得到整式串 $m$,$n$,$n - m$；第 $2$ 次操作后得到整式串 $m$,$n$,$n - m$,$-m$；第 $3$ 次操作后……其操作规则为每次操作增加的项,都是用上一次操作得到的最末项减去其前一项的差,小强将这个活动命名为“回头差”游戏。则该“回头差”游戏第 $2023$ 次操作后得到的整式串各项之和是( )

A.$m + n$
B.$m$
C.$n - m$
D.$2n$

答案： D

5 [2024 泰安中考]单项式 $-3ab^{2}$ 的次数是____。

答案： 3

6 [2024 德阳中考]若一个多项式加上 $y^{2}+3xy - 4$,结果是 $3xy + 2y^{2}-5$,则这个多项式为____。

答案： $y^{2}-1$

7 [2023 沈阳中考]当 $a + b = 3$ 时,代数式 $2(a + 2b)-(3a + 5b)+5$ 的值为____。

答案： 2

8 [2023 安徽中考节选]【观察思考】

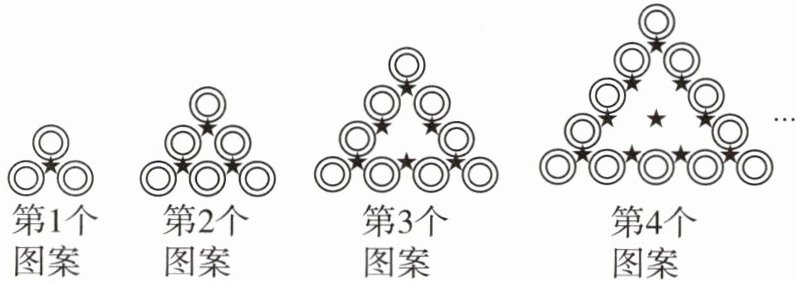
【规律发现】
请用含 $n$ 的式子填空：
(1)第 $n$ 个图案中“$◎$”的个数为____；
(2)第 $1$ 个图案中“$★$”的个数可表示为 $\frac{1×2}{2}$,第 $2$ 个图案中“$★$”的个数可表示为 $\frac{2×3}{2}$,第 $3$ 个图案中“$★$”的个数可表示为 $\frac{3×4}{2}$,第 $4$ 个图案中“$★$”的个数可表示为 $\frac{4×5}{2}$……第 $n$ 个图案中“$★$”的个数可表示为____。

答案：
(1)3n；
(2)$\frac{n(n+1)}{2}$

9 新趋势·代数推理 [2023 重庆中考 A 卷]如果一个四位自然数 $\overline{abcd}$ 的各数位上的数字互不相等且均不为 $0$,满足 $\overline{ab}-\overline{bc}= \overline{cd}$,那么称这个四位数为“递减数”。例如：四位数 $4129$,因为 $41 - 12 = 29$,所以 $4129$ 是“递减数”；又如：四位数 $5324$,因为 $53 - 32 = 21\neq24$,所以 $5324$ 不是“递减数”。若一个“递减数”为 $\overline{a312}$,则这个数为____；若一个“递减数”的前三个数字组成的三位数 $\overline{abc}$ 与后三个数字组成的三位数 $\overline{bcd}$ 的和能被 $9$ 整除,则满足条件的数的最大值是____。

答案： 4312；8165