《2025年一遍过七年级数学上册沪科版》

(1)下列说法可以用 $2(a + b)$ 表示的是( )

A.$a$ 的 $2$ 倍与 $b$ 的和
B.$a$ 与 $b$ 的 $2$ 倍的和
C.$a$ 与 $b$ 的和的 $2$ 倍
D.$2$ 与 $a$ 的乘积与 $b$ 的和

答案： C

(2)写出一个与 $-2ab$ 是同类项的单项式：____。

答案： ab(答案不唯一)

(3)多项式 $-2(a^{2}-2ab + b^{2})$ 去括号后的结果是____,这个结果是____次____项式,这个结果按字母 $b$ 的降幂排列是____。

答案： $-2a^{2}+4ab-2b^{2}$ 二 三 $-2b^{2}+4ab-2a^{2}$

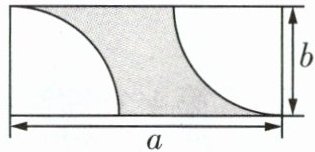
(4)在围成的长方形中,分别以它的两个顶点为圆心,$b$ m 为半径作两个不重叠的四分之一圆,如图。
①用代数式表示阴影部分的面积；
②当 $a = 10$,$b = 4$ 时,求阴影部分的面积。(结果保留 $\pi$)

答案： ①图中阴影部分的面积为$(ab-\frac {1}{2}\pi b^{2})m^{2}.$②当$a=10,b=4$时,阴影部分的面积为$ab-\frac {1}{2}\pi b^{2}=(40-8\pi )m^{2}.$

(5)若有理数 $a$,$b$ 在数轴上的位置如图所示,且 $c$ 为最大的负整数。化简：$\vert a - b\vert - 2\vert b - a + c\vert + 2\vert b - c\vert=$____。

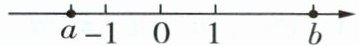
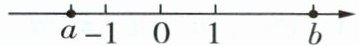
答案： $a+b+4$

(6)若 $a = b$,则用绳子围成的是正方形,下列图形都是由同样大小的正方形按一定规律组成的,其中第①个图形中一共有 $5$ 个正方形,第②个图形中一共有 $12$ 个正方形,第③个图形中一共有 $21$ 个正方形……按此规律排列,则第⑧个图形中正方形的个数为____。

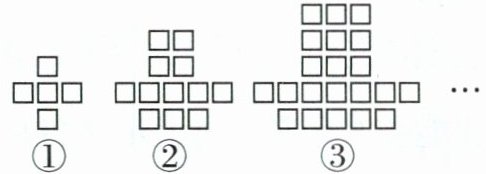
答案： 96

(7)若 $a$,$b$,$m$ 组成一个三位数 $\overline{abm}$,阅读下列材料,判断三位数 $\overline{abm}$ 能否被 $7$ 整除。
割尾法：三位数 $\overline{abm}$ 割掉末尾数字 $m$ 得两位数 $\overline{ab}$,再用 $\overline{ab}$ 减去 $m$ 的 $2$ 倍所得的差为 $\overline{ab}-2m$。若 $\overline{ab}-2m$ 是 $7$ 的倍数,则 $\overline{abm}$ 能被 $7$ 整除。
举例：对于三位数 $364$,割掉末尾数字 $4$ 得 $36$,$36 - 4×2 = 28$,因为 $28$ 是 $7$ 的倍数,所以 $364$ 能被 $7$ 整除。
【类比解决】尝试用“割尾法”判断 $455$ 能否被 $7$ 整除。
【推理验证】已知三位数 $\overline{abm}$。
①请用含 $a$,$b$,$m$ 的代数式表示“割尾法”后所得的差 $\overline{ab}-2m$；
②现在对材料中的判断方法“若 $\overline{ab}-2m$ 是 $7$ 的倍数,则 $\overline{abm}$ 能被 $7$ 整除”进行验证,下面是思路分析。
分析：要说明 $\overline{abm}$ 能被 $7$ 整除,需把 $\overline{abm}$ 表示成 $7$ 的倍数。已知 $\overline{abm}= 100a + 10b + m = 10(10a + b)+m$(i)。因为 $\overline{ab}-2m$ 是 $7$ 的倍数,可设 $\overline{ab}-2m = $ ①中的代数式 $=7k$($k$ 为整数)(ii)。只需把(ii)式变形代入(i)式即可。
请根据上述分析写出推理过程。

答案： 【类比解决】能.理由如下:对于三位数455,割掉末位数字5得45,$45-5×2=35$.因为35是7的倍数,所以455能被7整除.【推理验证】①因为$\overline {ab}=10a+b$,所以$\overline {ab}-2m=10a+b-2m.$②设$\overline {ab}-2m=10a+b-2m=7k$,所以$10a+b=7k+2m,$所以$\overline {abm}=100a+10b+m=10(10a+b)+m=10(7k+2m)+m=70k+21m=7(10k+3m),$所以$\overline {abm}$能被7整除.