第16页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
1 [2024 吉林中考]若$(-3)×□$的运算结果为正数,则□内的数字可以为 ( )
A.2
B.1
C.0
D.-1
A.2
B.1
C.0
D.-1
答案:
D由‘两数相乘,同号得正’可知□内的数字符号与-3相同,即负数,故选D.
2 [2025 蚌埠蚌山区段考]下列各式计算结果为负数的是 ( )
A.$5-(-3)$
B.$5+(-3)$
C.$5×(-3)$
D.$(-5)×(-3)$
A.$5-(-3)$
B.$5+(-3)$
C.$5×(-3)$
D.$(-5)×(-3)$
答案:
【解析】:
本题主要考察有理数的加、减、乘运算以及负数的识别。
A选项:$5-(-3)$,根据有理数的减法法则,减去一个负数等于加上这个数的绝对值,所以$5-(-3) = 5+3 = 8$,结果为正数,不符合题意。
B选项:$5+(-3)$,根据有理数的加法法则,异号相加取绝对值较大的数的符号,并用较大的绝对值减去较小的绝对值,所以$5+(-3) = 2$,结果为正数,不符合题意。
C选项:$5×(-3)$,根据有理数的乘法法则,正数乘以负数结果为负数,所以$5×(-3) = -15$,结果为负数,符合题意。
D选项:$(-5)×(-3)$,根据有理数的乘法法则,负数乘以负数结果为正数,所以$(-5)×(-3) = 15$,结果为正数,不符合题意。
综上所述,只有C选项的结果为负数。
【答案】:
C
本题主要考察有理数的加、减、乘运算以及负数的识别。
A选项:$5-(-3)$,根据有理数的减法法则,减去一个负数等于加上这个数的绝对值,所以$5-(-3) = 5+3 = 8$,结果为正数,不符合题意。
B选项:$5+(-3)$,根据有理数的加法法则,异号相加取绝对值较大的数的符号,并用较大的绝对值减去较小的绝对值,所以$5+(-3) = 2$,结果为正数,不符合题意。
C选项:$5×(-3)$,根据有理数的乘法法则,正数乘以负数结果为负数,所以$5×(-3) = -15$,结果为负数,符合题意。
D选项:$(-5)×(-3)$,根据有理数的乘法法则,负数乘以负数结果为正数,所以$(-5)×(-3) = 15$,结果为正数,不符合题意。
综上所述,只有C选项的结果为负数。
【答案】:
C
3 下列说法错误的是 ( )
A.一个数同 0 相乘,仍得 0
B.一个数同 1 相乘,仍得原数
C.一个数同 -1 相乘,得原数的相反数
D.互为相反数的两数之积为 1
A.一个数同 0 相乘,仍得 0
B.一个数同 1 相乘,仍得原数
C.一个数同 -1 相乘,得原数的相反数
D.互为相反数的两数之积为 1
答案:
【解析】:
本题主要考察有理数的乘法性质及相反数的定义。
A选项:根据有理数的乘法定义,任何数乘以0都等于0,所以A选项正确。
B选项:同样根据有理数的乘法定义,任何数乘以1都等于它本身,所以B选项正确。
C选项:一个数乘以-1,其结果为该数的相反数。例如,5乘以-1等于-5,-3乘以-1等于3,所以C选项正确。
D选项:互为相反数的两数之和为0,但它们的乘积并不一定是1。例如,5和-5是互为相反数,但它们的乘积是-25,不是1。所以D选项错误。
综上所述,错误的选项是D。
【答案】:
D
本题主要考察有理数的乘法性质及相反数的定义。
A选项:根据有理数的乘法定义,任何数乘以0都等于0,所以A选项正确。
B选项:同样根据有理数的乘法定义,任何数乘以1都等于它本身,所以B选项正确。
C选项:一个数乘以-1,其结果为该数的相反数。例如,5乘以-1等于-5,-3乘以-1等于3,所以C选项正确。
D选项:互为相反数的两数之和为0,但它们的乘积并不一定是1。例如,5和-5是互为相反数,但它们的乘积是-25,不是1。所以D选项错误。
综上所述,错误的选项是D。
【答案】:
D
4 [2025 合肥庐江县段考]在 2,-3,4,-5 这四个数中,任取两个数相乘,所得积的最大值是______.
答案:
【解析】:
本题考查了有理数的乘法。题目给出了四个数:2, -3, 4, -5,要求从这四个数中任取两个数相乘,并找出所得积的最大值。
首先,列出所有可能的数对组合,并计算它们的积:
$2 × (-3) = -6$
$2 × 4 = 8$
$2 × (-5) = -10$
$(-3) × 4 = -12$
$(-3) × (-5) = 15$
$4 × (-5) = -20$
从上面的计算中,可以看到最大的积是15。
【答案】:
15
本题考查了有理数的乘法。题目给出了四个数:2, -3, 4, -5,要求从这四个数中任取两个数相乘,并找出所得积的最大值。
首先,列出所有可能的数对组合,并计算它们的积:
$2 × (-3) = -6$
$2 × 4 = 8$
$2 × (-5) = -10$
$(-3) × 4 = -12$
$(-3) × (-5) = 15$
$4 × (-5) = -20$
从上面的计算中,可以看到最大的积是15。
【答案】:
15
5 计算:
(1)$(+6)×(-1)$;
(2)$(-36)×\frac {5}{6}$;
(3)$(-\frac {2}{3})×(-\frac {9}{10})$;
(4)$0.5×(-0.6)$;
(5)$-3\frac {5}{7}×0$;
(6)$\frac {17}{12}×(-0.8)$.
(1)$(+6)×(-1)$;
(2)$(-36)×\frac {5}{6}$;
(3)$(-\frac {2}{3})×(-\frac {9}{10})$;
(4)$0.5×(-0.6)$;
(5)$-3\frac {5}{7}×0$;
(6)$\frac {17}{12}×(-0.8)$.
答案:
【解析】:
本题考查了有理数的乘法法则,特别是乘法运算中正负数的处理以及分数与小数的乘法运算。
(1) 对于 $(+6)×(-1)$,根据有理数乘法法则,正数乘以负数得负数,所以结果为 $-6$。
(2) 对于 $(-36)×\frac{5}{6}$,首先确定符号为负,然后将36与6相约分,得到 $-6 × 5 = -30$。
(3) 对于 $(-\frac{2}{3})×(-\frac{9}{10})$,两个负数相乘得正数,然后进行分数的乘法运算,即 $\frac{2}{3} × \frac{9}{10} = \frac{18}{30}$,化简得 $\frac{3}{5}$。
(4) 对于 $0.5×(-0.6)$,正数乘以负数得负数,然后小数相乘,即 $0.5 × 0.6 = 0.3$,所以结果为 $-0.3$。
(5) 对于 $-3\frac{5}{7}×0$,任何数乘以0都得0,所以结果为0。
(6) 对于 $\frac{17}{12}×(-0.8)$,正数乘以负数得负数,然后将分数与小数相乘,即 $\frac{17}{12} × 0.8 = \frac{17 × 8}{12 × 10} = \frac{68}{60}$,化简得 $-\frac{17}{15}$,也可以表示为 $-1\frac{2}{15}$。
【答案】:
(1) $-6$
(2) $-30$
(3) $\frac{3}{5}$
(4) $-0.3$
(5) $0$
(6) $-1\frac{2}{15}$
本题考查了有理数的乘法法则,特别是乘法运算中正负数的处理以及分数与小数的乘法运算。
(1) 对于 $(+6)×(-1)$,根据有理数乘法法则,正数乘以负数得负数,所以结果为 $-6$。
(2) 对于 $(-36)×\frac{5}{6}$,首先确定符号为负,然后将36与6相约分,得到 $-6 × 5 = -30$。
(3) 对于 $(-\frac{2}{3})×(-\frac{9}{10})$,两个负数相乘得正数,然后进行分数的乘法运算,即 $\frac{2}{3} × \frac{9}{10} = \frac{18}{30}$,化简得 $\frac{3}{5}$。
(4) 对于 $0.5×(-0.6)$,正数乘以负数得负数,然后小数相乘,即 $0.5 × 0.6 = 0.3$,所以结果为 $-0.3$。
(5) 对于 $-3\frac{5}{7}×0$,任何数乘以0都得0,所以结果为0。
(6) 对于 $\frac{17}{12}×(-0.8)$,正数乘以负数得负数,然后将分数与小数相乘,即 $\frac{17}{12} × 0.8 = \frac{17 × 8}{12 × 10} = \frac{68}{60}$,化简得 $-\frac{17}{15}$,也可以表示为 $-1\frac{2}{15}$。
【答案】:
(1) $-6$
(2) $-30$
(3) $\frac{3}{5}$
(4) $-0.3$
(5) $0$
(6) $-1\frac{2}{15}$
6 [2024 陕西中考]-3 的倒数是 ( )
A.$-\frac {1}{3}$
B.$\frac {1}{3}$
C.-3
D.3
A.$-\frac {1}{3}$
B.$\frac {1}{3}$
C.-3
D.3
答案:
【解析】:
本题考查的是有理数的倒数概念。根据倒数的定义,一个数(0除外)的倒数等于1除以这个数。
因此,对于-3,其倒数应为1除以-3,即$-\frac{1}{3}$。
【答案】:
A. $-\frac{1}{3}$。
本题考查的是有理数的倒数概念。根据倒数的定义,一个数(0除外)的倒数等于1除以这个数。
因此,对于-3,其倒数应为1除以-3,即$-\frac{1}{3}$。
【答案】:
A. $-\frac{1}{3}$。
7 下列说法正确的是 ( )
A.$\frac {1}{4}$与 -0.25 互为倒数
B.$\frac {1}{4}$与 -4 互为倒数
C.0.1 与 10 互为倒数
D.0 的倒数是 0
A.$\frac {1}{4}$与 -0.25 互为倒数
B.$\frac {1}{4}$与 -4 互为倒数
C.0.1 与 10 互为倒数
D.0 的倒数是 0
答案:
【解析】:
本题主要考查有理数中倒数的概念。
根据倒数的定义,两个数的乘积为1时,这两个数互为倒数。需要验证每个选项中给出的两个数是否满足这一条件。
A. 验证$\frac{1}{4}$与-0.25的乘积:
$\frac{1}{4}× (-0.25) = -0.0625$
由于结果不为1,所以A选项错误。
B. 验证$\frac{1}{4}$与-4的乘积:
$\frac{1}{4} × (-4) = -1$
由于结果不为1,所以B选项错误。
C. 验证0.1与10的乘积:
$0.1 × 10 = 1$
由于结果为1,所以C选项正确。
D. 根据倒数的定义,0没有倒数,因为没有任何数与0相乘能得到1。所以D选项错误。
【答案】:
C
本题主要考查有理数中倒数的概念。
根据倒数的定义,两个数的乘积为1时,这两个数互为倒数。需要验证每个选项中给出的两个数是否满足这一条件。
A. 验证$\frac{1}{4}$与-0.25的乘积:
$\frac{1}{4}× (-0.25) = -0.0625$
由于结果不为1,所以A选项错误。
B. 验证$\frac{1}{4}$与-4的乘积:
$\frac{1}{4} × (-4) = -1$
由于结果不为1,所以B选项错误。
C. 验证0.1与10的乘积:
$0.1 × 10 = 1$
由于结果为1,所以C选项正确。
D. 根据倒数的定义,0没有倒数,因为没有任何数与0相乘能得到1。所以D选项错误。
【答案】:
C
8 [2024 亳州谯城区质检]倒数等于它本身的有理数是______.
答案:
【解析】:
本题考查有理数的乘法中倒数的概念。
设这个有理数为$x$,则根据倒数的定义,有$\frac{1}{x} = x$。
为了解这个方程,我们可以将方程两边同时乘以$x$(注意$x \neq 0$,因为0没有倒数):
$x \cdot \frac{1}{x} = x \cdot x$。
$1 = x^2$。
解得$x = \pm 1$。
因此,倒数等于它本身的有理数是$\pm 1$。
【答案】:
$\pm 1$。
本题考查有理数的乘法中倒数的概念。
设这个有理数为$x$,则根据倒数的定义,有$\frac{1}{x} = x$。
为了解这个方程,我们可以将方程两边同时乘以$x$(注意$x \neq 0$,因为0没有倒数):
$x \cdot \frac{1}{x} = x \cdot x$。
$1 = x^2$。
解得$x = \pm 1$。
因此,倒数等于它本身的有理数是$\pm 1$。
【答案】:
$\pm 1$。
9 [2025 上海宝山区期末]若 a,b 互为倒数,则$2ab-5= $______.
答案:
【解析】:
本题主要考察有理数的乘法运算以及倒数的概念。
首先,根据倒数的定义,如果两个数互为倒数,那么它们的乘积为1。
即,如果a和b互为倒数,那么有$ab = 1$。
接下来,我们将这个关系代入到给定的表达式$2ab-5$中。
代入$ab = 1$,我们得到:
$2ab - 5 = 2 × 1 - 5 = 2 - 5 = -3$
【答案】:
$-3$
本题主要考察有理数的乘法运算以及倒数的概念。
首先,根据倒数的定义,如果两个数互为倒数,那么它们的乘积为1。
即,如果a和b互为倒数,那么有$ab = 1$。
接下来,我们将这个关系代入到给定的表达式$2ab-5$中。
代入$ab = 1$,我们得到:
$2ab - 5 = 2 × 1 - 5 = 2 - 5 = -3$
【答案】:
$-3$
10 [2024 巴中中考]有理数 a,b 在数轴上对应点的位置如图所示,下列结论正确的是 ( )
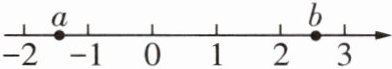
A.$ab>0$
B.$a+b<0$
C.$|a|>|b|$
D.$a-b<0$
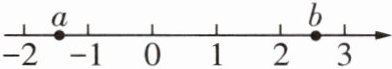
A.$ab>0$
B.$a+b<0$
C.$|a|>|b|$
D.$a-b<0$
答案:
【解析】:
由图可知,$a$ 在数轴上的位置在 -2 和 -1 之间,是一个负数;$b$ 在数轴上的位置在 2 和 3 之间,是一个正数。
接下来,我们逐一分析每个选项:
A. $ab \gt 0$
由于 $a$ 是负数,$b$ 是正数,根据有理数乘法法则,负数乘以正数结果是负数,所以 $ab \lt 0$,故 A 选项错误。
B. $a+b \lt 0$
由于 $a$ 是负数且其绝对值小于$b$的绝对值,$b$ 是正数,根据有理数加法法则,异号相加,取绝对值较大的数的符号,并用较大的绝对值减去较小的绝对值,所以 $a+b$ 的结果应为正数(因为 $b$ 的绝对值大于 $a$ 的绝对值),故 B 选项错误。
C. $|a| \gt |b|$
由图可知,$a$ 的绝对值(即 $a$ 到数轴原点的距离)小于 $b$ 的绝对值(即 $b$ 到数轴原点的距离),所以 $|a| \lt |b|$,故 C 选项错误。
D. $a-b \lt 0$
由于 $a$ 是负数,$b$ 是正数,根据有理数减法法则,减去一个数等于加上这个数的相反数,所以 $a-b = a+(-b)$,由于 $a$ 和 $-b$ 都是负数,所以 $a-b$ 的结果也是负数,即 $a-b \lt 0$,故 D 选项正确。
【答案】:
D
由图可知,$a$ 在数轴上的位置在 -2 和 -1 之间,是一个负数;$b$ 在数轴上的位置在 2 和 3 之间,是一个正数。
接下来,我们逐一分析每个选项:
A. $ab \gt 0$
由于 $a$ 是负数,$b$ 是正数,根据有理数乘法法则,负数乘以正数结果是负数,所以 $ab \lt 0$,故 A 选项错误。
B. $a+b \lt 0$
由于 $a$ 是负数且其绝对值小于$b$的绝对值,$b$ 是正数,根据有理数加法法则,异号相加,取绝对值较大的数的符号,并用较大的绝对值减去较小的绝对值,所以 $a+b$ 的结果应为正数(因为 $b$ 的绝对值大于 $a$ 的绝对值),故 B 选项错误。
C. $|a| \gt |b|$
由图可知,$a$ 的绝对值(即 $a$ 到数轴原点的距离)小于 $b$ 的绝对值(即 $b$ 到数轴原点的距离),所以 $|a| \lt |b|$,故 C 选项错误。
D. $a-b \lt 0$
由于 $a$ 是负数,$b$ 是正数,根据有理数减法法则,减去一个数等于加上这个数的相反数,所以 $a-b = a+(-b)$,由于 $a$ 和 $-b$ 都是负数,所以 $a-b$ 的结果也是负数,即 $a-b \lt 0$,故 D 选项正确。
【答案】:
D
11 [2025 阜阳段考]已知两个有理数 a,b,如果$ab<0且a+b>0$,那么 ( )
A.$a>0,b>0$
B.$a<0,b>0$
C.a,b 同号
D.a,b 异号,且正数的绝对值较大
A.$a>0,b>0$
B.$a<0,b>0$
C.a,b 同号
D.a,b 异号,且正数的绝对值较大
答案:
【解析】:
本题主要考察有理数的乘法性质以及绝对值的性质。
首先,根据有理数的乘法性质,当两个数的乘积小于0时,这两个数必定异号。即,如果$ab < 0$,那么a和b的符号必定不同。
其次,题目给出$a+b > 0$,即两个数的和大于0。由于a和b异号,那么这两个数相加要大于0,必须保证正数的绝对值大于负数的绝对值。
综合以上两点,我们可以得出结论:a和b异号,且正数的绝对值较大。
【答案】:
D. a,b 异号,且正数的绝对值较大。
本题主要考察有理数的乘法性质以及绝对值的性质。
首先,根据有理数的乘法性质,当两个数的乘积小于0时,这两个数必定异号。即,如果$ab < 0$,那么a和b的符号必定不同。
其次,题目给出$a+b > 0$,即两个数的和大于0。由于a和b异号,那么这两个数相加要大于0,必须保证正数的绝对值大于负数的绝对值。
综合以上两点,我们可以得出结论:a和b异号,且正数的绝对值较大。
【答案】:
D. a,b 异号,且正数的绝对值较大。
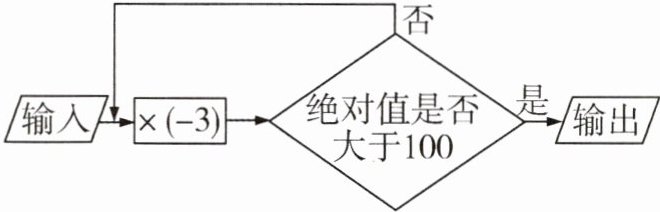
12 [2025 温州期中]按如图所示的程序计算,如果输入的数是 -2,那么输出的数是______.

答案:
【解析】:本题可根据程序图的运算规则,逐步计算输入值为$-2$时的输出结果。
首先,将输入的数$-2$乘以$-3$,得到$(-2)×(-3)=6$。
然后,判断$6$的绝对值是否大于$100$,因为$\vert6\vert = 6\lt100$,所以需要将$6$再次代入程序进行计算。
接着,将$6$乘以$-3$,得到$6×(-3)= -18$。
再判断$-18$的绝对值是否大于$100$,因为$\vert -18\vert = 18\lt100$,所以继续将$-18$代入程序计算。
将$-18$乘以$-3$,得到$(-18)×(-3)=54$。
判断$54$的绝对值是否大于$100$,因为$\vert54\vert = 54\lt100$,所以再将$54$代入程序计算。
将$54$乘以$-3$,得到$54×(-3)= -162$。
最后,判断$-162$的绝对值是否大于$100$,因为$\vert -162\vert = 162\gt100$,满足输出条件,所以输出的数是$-162$。
【答案】:$-162$
首先,将输入的数$-2$乘以$-3$,得到$(-2)×(-3)=6$。
然后,判断$6$的绝对值是否大于$100$,因为$\vert6\vert = 6\lt100$,所以需要将$6$再次代入程序进行计算。
接着,将$6$乘以$-3$,得到$6×(-3)= -18$。
再判断$-18$的绝对值是否大于$100$,因为$\vert -18\vert = 18\lt100$,所以继续将$-18$代入程序计算。
将$-18$乘以$-3$,得到$(-18)×(-3)=54$。
判断$54$的绝对值是否大于$100$,因为$\vert54\vert = 54\lt100$,所以再将$54$代入程序计算。
将$54$乘以$-3$,得到$54×(-3)= -162$。
最后,判断$-162$的绝对值是否大于$100$,因为$\vert -162\vert = 162\gt100$,满足输出条件,所以输出的数是$-162$。
【答案】:$-162$
查看更多完整答案,请扫码查看


