《2025年一遍过七年级数学上册沪科版》

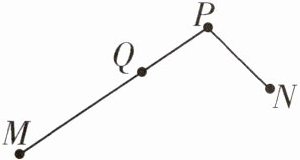
1 [2025合肥期末]如图,有公共端点P的两条线段MP,NP组成一条折线M—P—N,若该折线M—P—N上一点Q把这条折线分成相等的两部分,我们把这个点Q叫作这条折线的“折中点”.已知点D是折线A—C—B的“折中点”,点E为线段AC的中点,$CD= 3$,$CE= 5$,则线段BC的长为____.

答案：
4或16 分两种情况:①如图1,因为点D是折线A—C—B的“折中点”,所以AD=DC+CB,因为点E为线段AC的中点,所以AE=EC=$\frac{1}{2}$AC=5,所以AC=10,所以AD=AC - DC=7,所以DC+CB=7,所以BC=4;②如图2,因为点D是折线A—C—B的“折中点”,所以BD=DC+AC,因为点E为线段AC的中点,所以AE=EC=$\frac{1}{2}$AC=5,所以AC=10,所以AC+DC=13,所以BD=13,所以BC=BD+DC=16.综上所述,BC的长为4或16.
　　 　　　　

2 [2025亳州期末]作图与计算.
(1)如图,已知:$∠α$,$∠AOB$.
求作:以OA为一边,在$∠AOB的内部作∠AOC= ∠α$.(保留作图痕迹,不写作法)
(2)过点O作射线OD,若$∠AOB= 65^{\circ }$,$∠BOD= 30^{\circ }$,则$∠AOD$的度数为____.

答案：
解:
(1)如图所示,∠AOC即为所求的角.
　　　　　　　　　　　　　　　 　　　　　
(2)35°或95° 分两种情况讨论.如图1,当OD在∠AOB内部时,因为∠AOB=65°,∠BOD=30°,所以∠AOD=∠AOB - ∠BOD=65° - 30°=35°;如图2,当OD在∠AOB外部时,因为∠AOB=65°,∠BOD=30°,所以∠AOD=∠AOB+∠BOD=65°+30°=95°.综上,∠AOD的度数为35°或95°.
　　　　　　　　　　　　　　 　　

3 如图,$∠AOC与∠BOC$互余,OD平分$∠BOC$,$∠EOC= 2∠AOE$.
(1)若$∠AOD= 75^{\circ }$,求$∠AOE$的度数;
(2)若$∠DOE= 54^{\circ }$,求$∠EOC$的度数.

答案： 解:因为OD平分∠BOC,所以∠BOD=∠COD.因为∠AOC与∠BOC互余,所以∠AOB=∠AOC+∠BOC=90°.
(1)因为∠AOD=75°,所以∠BOD=90° - ∠AOD=15°,所以∠COD=∠BOD=15°,所以∠AOC=∠AOB - ∠BOC=90° - 2×15°=60°,即∠EOC+∠AOE=60°.因为∠EOC=2∠AOE,所以3∠AOE=60°,所以∠AOE=20°.
(2)设∠BOD=x,则∠COD=x,所以∠AOC=∠AOB - ∠BOC=90° - 2x.因为∠EOC=2∠AOE,所以∠EOC=$\frac{2}{3}$∠AOC=$\frac{2}{3}$(90° - 2x).因为∠DOE=54°,所以∠EOC+∠COD=$\frac{2}{3}$(90° - 2x)+x=54°,解得x=18°,所以∠EOC=36°.

4 如图,C是线段AB上一点,$AB= 12cm$,$AC= 4cm$,P,Q两点分别从点A,C出发,以$1cm/s$,$2cm/s$的速度沿直线AB向右运动,设运动时间为$ts$.
(1)当$t= 1$时,$CP= $____cm,$QB= $____cm.
(2)当t为多少时,PQ为AB的一半?
(3)当t为多少时,$BQ= AP$?

答案： 解:
(1)3 6 因为AB=12cm,AC=4cm,所以CB=12 - 4=8(cm).当t=1时,CP=4 - 1×1=3(cm),QB=8 - 2×1=6(cm).
(2)由题意,得AP=tcm,AQ=(4+2t)cm,所以4+2t - t=$\frac{1}{2}$×12,解得t=2.故当t为2时，PQ为AB的一半.
(3)由题意,得AP=tcm,BQ=|8 - 2t|cm,当BQ=AP时,有t=|8 - 2t|,解得t=8或$\frac{8}{3}$,故当t为8或$\frac{8}{3}$时,BQ=AP.

5 如图,点A在数轴上表示的数是-9,点D在数轴上表示的数是12,$AB= 4$(单位长度),$CD= 2$(单位长度).
(1)点B在数轴上表示的数是____,点C在数轴上表示的数是____,线段BC的长为____(单位长度);
(2)若点P是线段BC的中点,则点P在数轴上表示的数是____;
(3)若点Q是数轴上的点,且$QC= 2QB$,则点Q在数轴上表示的数是____.

答案：
(1)-5 10 15;
(2)2.5;
(3)0或 - 20
(1)因为 - 9+4=-5,所以点B在数轴上表示的数是 - 5.因为12 - 2=10,所以点C在数轴上表示的数是10.因为10 - (-5)=10+5=15,所以线段BC的长为15(单位长度).
(2)设点P在数轴上表示的数是x,因为点P是线段BC的中点,所以BP=CP,所以10 - x=x - (-5),所以10 - x=x+5,所以x=2.5,所以点P在数轴上表示的数是2.5.
(3)设点Q在数轴上表示的数是a,分两种情况:当点Q在点B的右侧时,因为QC=2QB,所以10 - a=2[a - (-5)],所以a=0;当点Q在点B的左侧时,因为QC=2QB,所以10 - a=2(-5 - a),所以a=-20.综上,点Q在数轴上表示的数是0或 - 20.