第76页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
7 [2024绵阳期末]某工厂有m名工人,每名工人每天能加工6个A型零件或者3个B型零件,其中某产品每套由4个A型零件和3个B型零件配套组成,现将工人分成两组,每组分别只加工一种零件,并要求每天加工的零件正好配套,现50天恰好完成1200套产品的生产任务,则m的值为 ( )
A.30
B.40
C.50
D.60
A.30
B.40
C.50
D.60
答案:
B 设安排x名工人加工A型零件,则安排(m-x)名工人加工B型零件,根据题意,得{3×6x=4×3(m-x),50×[6x+3(m-x)]=1200×(3+4)整理,得{5x=2m,x+m=56,解得{x=16,m=40.
8 [2025滁州一模]茶叶是我省西南地区的特产,某村部分青年返乡创业生产销售A,B两种茶叶,去年年初制订的计划是完成总销售利润200万元.经过努力,其中生产销售A种茶叶的利润比原计划增加5%,生产销售B种茶叶的利润比原计划增加15%,实际生产销售的总利润为225万元,他们去年生产销售A,B两种茶叶实际完成的销售利润各多少万元?
答案:
解:设他们去年计划生产销售A种茶叶的销售利润为x万元,B种茶叶的销售利润为y万元,
根据题意,得{x+y=200,(1+5%)x+(1+15%)y=225,解得{x=50,y=150,
所以(1+5%)x=(1+5%)×50=52.5,(1+15%)y=(1+15%)×150=172.5.
答:他们去年生产销售A,B两种茶叶实际完成的销售利润分别为52.5万元,172.5万元.
根据题意,得{x+y=200,(1+5%)x+(1+15%)y=225,解得{x=50,y=150,
所以(1+5%)x=(1+5%)×50=52.5,(1+15%)y=(1+15%)×150=172.5.
答:他们去年生产销售A,B两种茶叶实际完成的销售利润分别为52.5万元,172.5万元.
9 某工厂计划生产甲、乙两种季节性产品,在春季中,甲种产品售价为50千元/件,乙种产品售价为30千元/件,生产这两种产品需要A,B两种原料.
| |A种原料/(吨/件)|B种原料/(吨/件)|
|甲产品|4|2|
|乙产品|3|1|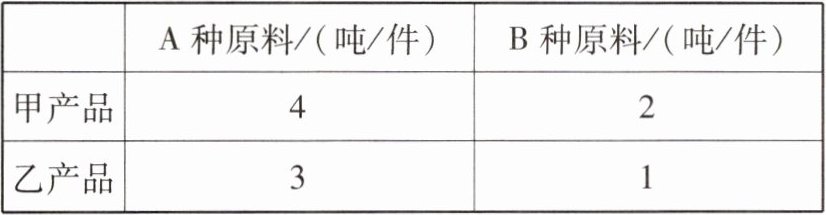
每个季节该厂能获得A种原料120吨,B种原料50吨.
(1)如何安排生产,才能恰好使两种原料全部用完?此时总产值是多少万元?
(2)在夏季中甲种产品售价上涨10%,而乙种产品售价下降10%,并且要求甲种产品比乙种产品多生产20件,如何安排甲、乙两种产品的生产,能使总产值是1264千元?
| |A种原料/(吨/件)|B种原料/(吨/件)|
|甲产品|4|2|
|乙产品|3|1|

每个季节该厂能获得A种原料120吨,B种原料50吨.
(1)如何安排生产,才能恰好使两种原料全部用完?此时总产值是多少万元?
(2)在夏季中甲种产品售价上涨10%,而乙种产品售价下降10%,并且要求甲种产品比乙种产品多生产20件,如何安排甲、乙两种产品的生产,能使总产值是1264千元?
答案:
(1)设生产甲种产品x件、乙种产品y件.
根据题意,得{4x+3y=120,2x+y=50,解得{x=15,y=20.
15×50+30×20=750+600=1350(千元),
1350千元=135万元.
答:生产甲种产品15件、乙种产品20件才能恰好使两种原料全部用完,此时总产值是135万元.
(2)设生产甲种产品m件、乙种产品n件.
根据题意,得{m-n=20,(1+10%)×50m+(1-10%)×30n=1264,解得{m=22,n=2.
此时消耗A原料22×4+2×3=94(吨),
消耗B原料22×2+2×1=46(吨),
因为94<120,46<50,所以这样安排可行.
答:生产甲种产品22件、乙种产品2件,可使总产值是1264千元.
(1)设生产甲种产品x件、乙种产品y件.
根据题意,得{4x+3y=120,2x+y=50,解得{x=15,y=20.
15×50+30×20=750+600=1350(千元),
1350千元=135万元.
答:生产甲种产品15件、乙种产品20件才能恰好使两种原料全部用完,此时总产值是135万元.
(2)设生产甲种产品m件、乙种产品n件.
根据题意,得{m-n=20,(1+10%)×50m+(1-10%)×30n=1264,解得{m=22,n=2.
此时消耗A原料22×4+2×3=94(吨),
消耗B原料22×2+2×1=46(吨),
因为94<120,46<50,所以这样安排可行.
答:生产甲种产品22件、乙种产品2件,可使总产值是1264千元.
10 [2025阜阳段考]随着“低碳生活,绿色出行”理念的普及,新能源汽车正逐渐成为人们喜爱的交通工具.某汽车销售公司计划购进一批新能源汽车尝试进行销售,据了解2辆A型汽车、3辆B型汽车的进价共计80万元;3辆A型汽车、2辆B型汽车的进价共计95万元.
(1)求A,B两种型号的汽车每辆进价分别为多少万元.
(2)若该公司计划正好用200万元购进以上两种型号的新能源汽车(两种型号的汽车均购买),请你帮助该公司设计购买方案.
(3)若该汽车销售公司销售1辆A型汽车可获利8000元,销售1辆B型汽车可获利5000元,在(2)中的购买方案中,假如这些新能源汽车全部售出,哪种方案获利最大?最大利润是多少元?
(1)求A,B两种型号的汽车每辆进价分别为多少万元.
(2)若该公司计划正好用200万元购进以上两种型号的新能源汽车(两种型号的汽车均购买),请你帮助该公司设计购买方案.
(3)若该汽车销售公司销售1辆A型汽车可获利8000元,销售1辆B型汽车可获利5000元,在(2)中的购买方案中,假如这些新能源汽车全部售出,哪种方案获利最大?最大利润是多少元?
答案:
(1)设A型汽车每辆的进价为x万元,B型汽车每辆的进价为y万元.
依题意,得{2x+3y=80,3x+2y=95,解得{x=25,y=10.
答:A型汽车每辆的进价为25万元,B型汽车每辆的进价为10万元.
(2)设购进A型汽车m辆,购进B型汽车n辆,
依题意,得25m+10n=200,所以m=8-25n.
因为m,n均为正整数,所以n为5的倍数,
所以25m+10n=200的正整数解为{m=6,n=5或{m=4,n=10或{m=2,n=15.
所以共有3种购买方案,
方案一:购进A型汽车6辆、B型汽车5辆;
方案二:购进A型汽车4辆、B型汽车10辆;
方案三:购进A型汽车2辆、B型汽车15辆.
(3)方案一获得利润:8000×6+5000×5=73000(元);
方案二获得利润:8000×4+5000×10=82000(元);
方案三获得利润:8000×2+5000×15=91000(元).
因为73000<82000<91000,
所以购进A型汽车2辆、B型汽车15辆获利最大,最大利润是91000元.
(1)设A型汽车每辆的进价为x万元,B型汽车每辆的进价为y万元.
依题意,得{2x+3y=80,3x+2y=95,解得{x=25,y=10.
答:A型汽车每辆的进价为25万元,B型汽车每辆的进价为10万元.
(2)设购进A型汽车m辆,购进B型汽车n辆,
依题意,得25m+10n=200,所以m=8-25n.
因为m,n均为正整数,所以n为5的倍数,
所以25m+10n=200的正整数解为{m=6,n=5或{m=4,n=10或{m=2,n=15.
所以共有3种购买方案,
方案一:购进A型汽车6辆、B型汽车5辆;
方案二:购进A型汽车4辆、B型汽车10辆;
方案三:购进A型汽车2辆、B型汽车15辆.
(3)方案一获得利润:8000×6+5000×5=73000(元);
方案二获得利润:8000×4+5000×10=82000(元);
方案三获得利润:8000×2+5000×15=91000(元).
因为73000<82000<91000,
所以购进A型汽车2辆、B型汽车15辆获利最大,最大利润是91000元.
查看更多完整答案,请扫码查看


