《2025年一遍过七年级数学上册沪科版》

1 教材 P118 例 1 变式 [2025 深圳龙岗区期末]“市长杯”青少年校园足球联赛的比赛规则是:胜一场得 3 分,平一场得 1 分,负一场得 0 分.某校足球队在第一轮比赛中赛了 9 场,只负了 2 场,共得 17 分.那么该队胜了几场,平了几场?设该队胜了 x 场,平了 y 场,根据题意可列方程组为 ( )

A.$\left\{\begin{array}{l} x+y= 7,\\ 3x+y= 17\end{array} \right.$
B.$\left\{\begin{array}{l} x+y= 9,\\ 3x+y= 17\end{array} \right.$
C.$\left\{\begin{array}{l} x+y= 7,\\ x+3y= 17\end{array} \right.$
D.$\left\{\begin{array}{l} x+y= 9,\\ x+3y= 17\end{array} \right.$

答案： A

2 一题多解 一份试卷共 25 道题,每道题都给出四个答案,其中只有一个是正确的,要求学生把正确答案选出来,每道题选对得 4 分,不选或选错扣 1 分,如果一个学生得 90 分,那么他选对了几道题?

答案： 解:通解设他选对了x道题,不选或选错了y道题.
根据题意,得{x+y=25,\n4x−y=90.解得{x=23,\ny=2.\n答:他选对了23道题.\n另解设他选对了x道题,则不选或选错了(25−x)道题.\n根据题意$4x−(25−x)=90$,解得x=23.\n答:他选对了23道题.

3 甲、乙两人分别从相距 20 km 的 A,B 两地出发,相向而行.如图是小华绘制的甲、乙两人两次运动的情形.设甲的速度是 x km/h,乙的速度是 y km/h,根据题意可列方程组为______.

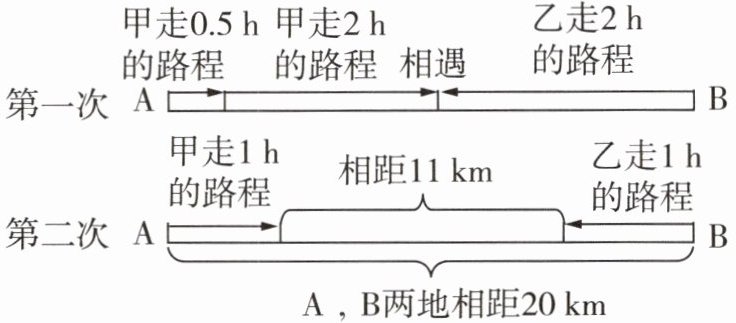
答案： 解：根据题意，第一次运动中，甲先出发0.5小时，之后甲、乙共同行走2小时相遇，甲总共行走的时间为$0.5 + 2 = 2.5$小时，乙行走2小时，两人路程之和为20km，可得方程$2.5x + 2y = 20$；第二次运动中，甲、乙同时出发1小时后相距11km，两人1小时行走的路程之和为$20 - 11 = 9$km，可得方程$x + y = 9$。
综上，可列方程组为$\begin{cases}2.5x + 2y = 20 \\ x + y = 9\end{cases}$

4 一题多解 从 A 地到 B 地全程 290 km,前一路段为国道,其余路段为高速公路.已知一辆汽车在国道上行驶的速度为 60 km/h,在高速公路上行驶的速度为 100 km/h,该辆汽车从 A 地开往 B 地一共行驶了 3.5 h.求 A,B 两地间国道和高速公路长分别是多少千米.

答案： 解:通解设A,B两地间国道和高速公路长分别是xkm,\nykm.\n依题意,得{x + y = 290,\n$\frac{x}{60}+\frac{y}{100}=3.5$,解得{x=90,\ny=200.\n答:A,B两地间国道和高速公路长分别是90km,200km.\n另解设该辆汽车在国道上行驶的时间为xh,在高速公路上行驶的时间为yh.\n依题意,得{x + y = 3.5,\n60x + 100y = 290,解得{x=1.5,\ny=2.\n则A,B两地间国道长是1.5×60=90(km),高速公路长是100×2=200(km).\n答:A,B两地间国道长90km,高速公路长200km.

5 一题多解 [2025 武汉汉阳区期中]在文具店,若买 2 个橡皮、1 支铅笔共需 4 元;若买 1 个橡皮、2 支铅笔共需 5 元,则买一个橡皮和一支铅笔共需 ( )

A.3 元
B.4 元
C.5 元
D.6 元

答案： A

6 [2025 宿州期末]为创建“绿色校园”,绿化校园环境,某校计划分两次购进 A,B 两种花草,第一次分别购进 A,B 两种花草 30 棵和 15 棵,共花费 675 元,第二次分别购进 A,B 两种花草 12 棵和 5 棵,共花费 265 元(两次购进同种花草和价格相同).那么 A,B 两种花草每棵的价格分别是多少元?

答案： 【解析】：
本题主要考查二元一次方程组的应用。
设A种花草每棵的价格为$x$元，B种花草每棵的价格为$y$元。
根据题意，第一次购进A、B两种花草的费用可以表示为$30x + 15y$，第二次购进的费用可以表示为$12x + 5y$。
因此，我们可以列出以下方程组：
$\begin{cases}30x + 15y = 675 \\12x + 5y = 265\end{cases}$
为了解这个方程组，我们可以使用消元法或代入法。
这里我们使用消元法，先将第一个方程除以5，第二个方程除以1，得到：
$\begin{cases}6x + 3y = 135 \\12x + 5y = 265\end{cases}$
然后用第二个新方程减去第一个新方程的两倍，得到：
$12x + 5y - 2(6x + 3y) = 265 - 2 × 135$
$12x + 5y - 12x - 6y = 265 - 270$
$-y = -5$
$y = 5$
将$y = 5$代入第一个新方程$6x + 3y = 135$，解得：
$6x + 3 × 5 = 135$
$6x + 15 = 135$
$6x = 120$
$x = 20$
所以，A种花草每棵的价格是20元，B种花草每棵的价格是5元。
【答案】：
A种花草每棵的价格是20元，B种花草每棵的价格是5元。