第37页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
1 [2025亳州谯城区期末]若$m= -1$,则$5m^{3}-2m$的值为 ( )
A.-3
B.3
C.-7
D.7
A.-3
B.3
C.-7
D.7
答案:
A 当m=-1时,5m³-2m=5×(-1)³-2×(-1)=-3.
2 [2023无锡中考]当$a= 2,b= -3$时,代数式$(a-b)^{2}+2ab$的值为 ( )
A.13
B.27
C.-5
D.-7
A.13
B.27
C.-5
D.-7
答案:
A 当a=2,b=-3时,(a-b)²+2ab=[2-(-3)]²+2×2×(-3)=25-12=13.
3 [2025合肥庐阳区期中]按照如图所示的计算程序,若$x= 2$,则输出的结果是 ( )

A.16
B.26
C.-16
D.-26

A.16
B.26
C.-16
D.-26
答案:
D 输入x=2,得10-x²=10-4=6>0,不输出;继续输入x=6,得10-x²=10-36=-26<0,输出-26.
4 [2024合肥瑶海区期末]已知$a^{2}-2a-2= 0$,则$3(a^{2}-2a)+6$的值为____.
答案:
12 因为a²-2a-2=0,所以a²-2a=2,所以3(a²-2a)(整体代入)+6=3×2+6=12.
5 [2025芜湖期中]人在运动时,心跳速率通常和人的年龄有关,如果用x表示一个人的年龄,用y表示正常情况下这个人在运动时所能承受的每分钟心跳的最多次数,假设y与x存在关系式:$y= \frac {4}{5}(220-x).$
(1)正常情况下,一个15岁的少年在运动时,所能承受的每分钟心跳的最多次数是多少?
(2)一个50岁的人运动时,30秒钟心跳的最多次数为60次,他有危险吗? 请说明你的理由.
(1)正常情况下,一个15岁的少年在运动时,所能承受的每分钟心跳的最多次数是多少?
(2)一个50岁的人运动时,30秒钟心跳的最多次数为60次,他有危险吗? 请说明你的理由.
答案:
解:
(1)当x=15时,y=4/5(220-x)=4/5×(220-15)=164,即正常情况下,一个15岁的少年在运动时,所能承受的每分钟心跳的最多次数是164.
(2)他没有危险.理由如下:
当x=50时,y=4/5(220-x)=4/5×(220-50)=136.
因为他运动时,30秒心跳的最多次数是60次,所以他每分钟心跳的最多次数是120次.
因为136>120,所以他没有危险.
(1)当x=15时,y=4/5(220-x)=4/5×(220-15)=164,即正常情况下,一个15岁的少年在运动时,所能承受的每分钟心跳的最多次数是164.
(2)他没有危险.理由如下:
当x=50时,y=4/5(220-x)=4/5×(220-50)=136.
因为他运动时,30秒心跳的最多次数是60次,所以他每分钟心跳的最多次数是120次.
因为136>120,所以他没有危险.
6 [2025石家庄期末]下列代数式,满足表中条件的是 ( )
|x|0|1|2|3|
|代数式的值|-3|-1|1|3|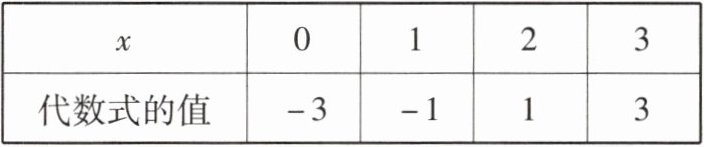
A.$-x-3$
B.$x^{2}+2x-3$
C.$2x-3$
D.$x^{2}-2x-3$
|x|0|1|2|3|
|代数式的值|-3|-1|1|3|

A.$-x-3$
B.$x^{2}+2x-3$
C.$2x-3$
D.$x^{2}-2x-3$
答案:
C
7 已知多项式$A= 2025x^{2}+2026x+m和B= 2026x^{2}+2025x+m$,下列三个判断中一定正确的是____.(填序号)
①当$x= 1$时,$A= B$.
②当$x= -1$时,$A+B= 0$.
③当x为任意有理数时,B的值总大于A的值.
①当$x= 1$时,$A= B$.
②当$x= -1$时,$A+B= 0$.
③当x为任意有理数时,B的值总大于A的值.
答案:
① 当x=1时,A=2025+2026+m,B=2026+2025+m,此时A=B,故①正确.当x=-1时,A+B=2025-2026+m+2026-2025+m=2m,故②错误.当x=0时,B=A,故③错误
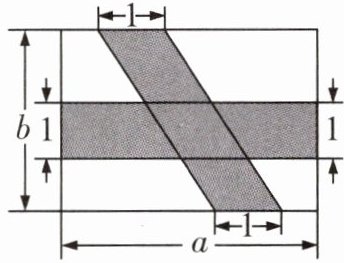
8 教材P71练习T2变式[2024滁州期末]如图是一个长为a,宽为b的长方形,两个阴影图形都是一对底边长为1,且底边在长方形对边上的平行四边形.
(1)用含字母a,b的代数式表示长方形中空白部分的面积;
(2)当$a= 3,b= 2$时,求长方形中空白部分的面积.
(1)用含字母a,b的代数式表示长方形中空白部分的面积;
(2)当$a= 3,b= 2$时,求长方形中空白部分的面积.

答案:
解:
(1)将题图中阴影部分平移,可知空白部分的面积为(a-1)(b-1).
(2)当a=3,b=2时,空白部分の面积为(3-1)(2-1)=2.
(1)将题图中阴影部分平移,可知空白部分的面积为(a-1)(b-1).
(2)当a=3,b=2时,空白部分の面积为(3-1)(2-1)=2.
查看更多完整答案,请扫码查看


