《2025年一遍过七年级数学上册沪科版》

8 [2025合肥瑶海区期中]若$A = 2x^{2} + x + 1$,$B = x^{2} + x$,则$A$,$B$的大小关系是( )

A.$A ＞ B$
B.$A ＜ B$
C.$A = B$
D.不能确定

答案： A 因为A=2x²+x+1,B=x²+x,所以A-B=(2x²+x+1)-(x²+x)=2x²+x+1-x²-x=x²+1.因为x²≥0,所以x²+1＞0,所以A-B＞0,即A＞B.

9 [2025莆田荔城区期末]已知$6y - x = -5$,则$(x + 2y) - 2(x - 2y) = $( )

A.$-5$
B.$5$
C.$3$
D.$2$

答案： A (x+2y)-2(x-2y)=x+2y-2x+4y=6y-x,因为6y-x=-5,所以原式=-5.

10 [2025安庆期末]若$A$,$B$都是四次多项式,则$A + B$一定是( )

A.八次多项式
B.次数不低于4的多项式
C.四次多项式
D.次数不高于4的多项式或单项式

答案： D A+B的最高次数可能是4,最低次数可能是0,即为常数.

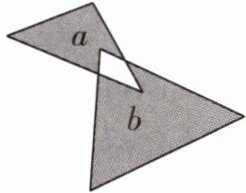
11 [2025安庆期末]如图,两个三角形的面积分别为7和18,两阴影部分的面积分别为$a$,$b$($a ＜ b$),则$a - b$的值为____。

答案： -11 设重合的空白部分的面积为m,由题图可得,a=7-m,b=18-m,所以a-b=7-m-(18-m)=-11.

12 [2025合肥蜀山区期中]有一个程序指令,当任意数对$(m, n)$放入其中,会得到一个新的数：$-3m + 2n + 1$.例如把$(-2, 1)$放入其中,就会得到$-3×(-2) + 2×1 + 1 = 9$.
(1)现将数对$(3, 2)$放入其中,得到的数为$a$,再将$(a, -5)$放入其中,则得到的新数是____；
(2)若将$(ax - 2, -3x + 1)$放入其中,得到的式子中不含$x$项,则$a$的值为____。

答案：
(1)3;
(2)-2
(1)把数对(3,2)放入其中,得a=-3×3+2×2+1=-9+4+1=-4,再将(-4,-5)放入其中,得到的新数为-3×(-4)+2×(-5)+1=12+(-10)+1=3.
(2)将(ax-2,-3x+1)放入其中,得到的式子为-3(ax-2)+2(-3x+1)+1=-3ax+6-6x+2+1=(-3a-6)x+9,因为得到的式子中不含x项,所以-3a-6=0,-3a=6,a=-2.

13 [2025合肥庐阳区期中]已知一个三角形院墙,第一条边长为$(5a + 2b)$米,第二条边比第一条边长$(a - b)$米,第三条边比第二条边短$2a$米.
(1)第二条边长为____米,第三条边长为____米.(用含有$a$,$b$的式子表示)
(2)当$a = 2$,$b = 1$时,这个三角形的周长是多少米？
(3)在(2)的条件下,围成院墙的材料20米以内收费每米180元,超过20米的部分每米收费150元,请问围成这个三角形的院墙至少要花费多少钱？

答案： 解:
(1)(6a+b) (4a+b)
由题意得,第二条边长为5a+2b+(a-b)=6a+b(米),第三条边长为6a+b-2a=4a+b(米).
(2)这个三角形的周长为
(5a+2b)+(6a+b)+(4a+b)
=5a+2b+6a+b+4a+b
=15a+4b,
当a=2,b=1时,原式=15×2+4×1=30+4=34,
即这个三角形的周长是34米.
(3)因为34＞20,所以围成这个三角形的院墙至少要花费20×180+(34-20)×150=3600+2100=5700(元).

14 几何直观 在如图所示的数轴(缺原点)上$A点表示数a$,$B点表示数b$,$C点表示数c$,$b$是最小的正整数,且$a$,$c满足|a + 2| + (c - 7)^{2} = 0$.

(1)$a = $____,$b = $____,$c = $____。
(2)点$A$,$B$,$C$开始在数轴上运动,若点$A$以每秒1个单位长度的速度向左运动,同时,点$B和点C$分别以每秒2个单位长度和每秒4个单位长度的速度向右运动.设$t$秒过后,点$A与点B之间的距离表示为AB$,点$A与点C之间的距离表示为AC$,点$B与点C之间的距离表示为BC$,则$AB = $____,$AC = $____,$BC = $____.(用含$t$的代数式表示)
追问：$3BC - 2AB的值是否随着时间t$的变化而改变？若改变,请说明理由；若不变,请求其值。

答案： 解:
(1)-2 1 7
因为|a+2|+(c-7)²=0,所以a+2=0,c-7=0,所以a=-2,c=7.因为b是最小的正整数,所以b=1.
(2)3t+3 5t+9 2t+6
由题意知,t秒过后,点A表示的数为-2-t,点B表示的数为1+2t,点C表示的数为7+4t,所以AB=1+2t-(-2-t)=1+2t+2+t=3t+3,AC=7+4t-(-2-t)=7+4t+2+t=5t+9,BC=7+4t-(1+2t)=7+4t-1-2t=2t+6.
追问:不变.
3BC-2AB=3(2t+6)-2(3t+3)=6t+18-6t-6=12.