第89页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
9 [2025汕头龙湖区期末]如图是某住宅小区的平面图,点B是该小区“菜鸟驿站”的位置,其余各点为居民楼的位置,图中各条线为小区内的小路,从居民楼点A到“菜鸟驿站”点B的最短路径是( )

A.$A-C-G-E-B$
B.$A-C-E-B$
C.$A-D-G-E-B$
D.$A-F-E-B$

A.$A-C-G-E-B$
B.$A-C-E-B$
C.$A-D-G-E-B$
D.$A-F-E-B$
答案:
D
10 如图,已知B是线段AC上的一点,M是线段AB的中点,N是线段AC的中点,P是线段AN的中点,Q是线段AM的中点,则$MN:PQ$等于( )
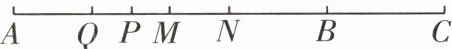
A.$1:1$
B.$2:1$
C.$3:1$
D.$4:1$
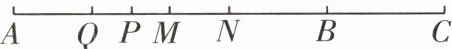
A.$1:1$
B.$2:1$
C.$3:1$
D.$4:1$
答案:
B 因为P是线段AN的中点,Q是线段AM的中点,所以AP=$\frac{1}{2}$AN,AQ=$\frac{1}{2}$AM,所以PQ=AP-AQ=$\frac{1}{2}$AN-$\frac{1}{2}$AM=$\frac{1}{2}$(AN-AM)=$\frac{1}{2}$MN,所以MN:PQ=2:1.
11 [2025安庆期末]如图,C是线段AB上的一点,D是BC中点,已知图中所有线段长度之和为23.

(1)设线段BD的长为x,则线段$AC= $____.(用含x的代数式表示).
(2)若线段AC,BD的长度都是正整数,则线段AC的长为____.

(1)设线段BD的长为x,则线段$AC= $____.(用含x的代数式表示).
(2)若线段AC,BD的长度都是正整数,则线段AC的长为____.
答案:
(1)$\frac{23-7x}{3}$;
(2)3 解题思路:
(1)由中点的定义可得CD=x,BC=2x,AD=AC+CD=AC+x,AB=AC+CB=AC+2x,由题意可得AC+CD+DB+AD+AB+CB=23,等量代换即可求解;
(2)由
(1)结论可知AC=$\frac{23-7x}{3}$,根据正整数的定义即可求解.
(1)因为D是BC中点,所以CD=BD=x,BC=2BD=2x,所以AD=AC+CD=AC+x,AB=AC+CB=AC+2x,因为AC+CD+DB+AD+AB+CB=23(不重不漏找出题图中所有线段),所以AC+x+x+AC+x+AC+2x+2x=23,即3AC+7x=23,所以AC=$\frac{23-7x}{3}$.
(2)因为线段AC,BD的长度都是正整数,所以$\frac{23-7x}{3}$>0,x>0,所以x可能为1,2,3.当x=1时,$\frac{23-7x}{3}$是小数,不符合题意,舍去;当x=2时,$\frac{23-7x}{3}$=3,符合题意;当x=3时,$\frac{23-7x}{3}$是小数,不符合题意,舍去.综上,AC的长为3.
(1)$\frac{23-7x}{3}$;
(2)3 解题思路:
(1)由中点的定义可得CD=x,BC=2x,AD=AC+CD=AC+x,AB=AC+CB=AC+2x,由题意可得AC+CD+DB+AD+AB+CB=23,等量代换即可求解;
(2)由
(1)结论可知AC=$\frac{23-7x}{3}$,根据正整数的定义即可求解.
(1)因为D是BC中点,所以CD=BD=x,BC=2BD=2x,所以AD=AC+CD=AC+x,AB=AC+CB=AC+2x,因为AC+CD+DB+AD+AB+CB=23(不重不漏找出题图中所有线段),所以AC+x+x+AC+x+AC+2x+2x=23,即3AC+7x=23,所以AC=$\frac{23-7x}{3}$.
(2)因为线段AC,BD的长度都是正整数,所以$\frac{23-7x}{3}$>0,x>0,所以x可能为1,2,3.当x=1时,$\frac{23-7x}{3}$是小数,不符合题意,舍去;当x=2时,$\frac{23-7x}{3}$=3,符合题意;当x=3时,$\frac{23-7x}{3}$是小数,不符合题意,舍去.综上,AC的长为3.
12 [2024六安期末]如图1,已知点M是线段AB上一点,C,D两点分别从M,B同时出发分别以1 cm/s,3 cm/s的速度沿线段BA向左运动,且点C在线段AM上,点D在线段BM上.
(1)若$AB= 10cm$,当点C,D运动2 s时,$AC+MD= $____cm.
(2)当点C,D运动时,总有$MD= 3AC$,则$AM= $____AB.
(3)如图2,若$AM= \frac {1}{4}AB$,点N是直线AB上一点,且$AN-BN= MN$,求$\frac {MN}{AB}$的值.

(1)若$AB= 10cm$,当点C,D运动2 s时,$AC+MD= $____cm.
(2)当点C,D运动时,总有$MD= 3AC$,则$AM= $____AB.
(3)如图2,若$AM= \frac {1}{4}AB$,点N是直线AB上一点,且$AN-BN= MN$,求$\frac {MN}{AB}$的值.

答案:
解:
(1)2
当点C,D运动2 s时,CM=2 cm,BD=6 cm,因为AB=10 cm,所以AC+MD=AB-CM-BD=10-2-6=2(cm).
(2)$\frac{1}{4}$
因为C,D两点运动的速度分别为1 cm/s,3 cm/s,所以BD=3CM,又因为MD=3AC,所以BD+MD=3CM+3AC,所以BM=3AM,所以AM=$\frac{1}{4}$AB.
(3)当点N在线段AB上时,如图1,因为AN-BN=MN,AN=AM=MN,所以BN=AM=$\frac{1}{4}$AB,所以MN=$\frac{1}{2}$AB,即$\frac{MN}{AB}$=$\frac{1}{2}$.
A M N B(图略)
当点N在线段AB 的延长线上时,如图2,因为AN-BN=MN,AN-BN=AB,所以MN=AB,即$\frac{MN}{AB}$=1.
A M B N(图略)综上所述,$\frac{MN}{AB}$的值为$\frac{1}{2}$或1.A M N B图1
A M B N图2
(1)2
当点C,D运动2 s时,CM=2 cm,BD=6 cm,因为AB=10 cm,所以AC+MD=AB-CM-BD=10-2-6=2(cm).
(2)$\frac{1}{4}$
因为C,D两点运动的速度分别为1 cm/s,3 cm/s,所以BD=3CM,又因为MD=3AC,所以BD+MD=3CM+3AC,所以BM=3AM,所以AM=$\frac{1}{4}$AB.
(3)当点N在线段AB上时,如图1,因为AN-BN=MN,AN=AM=MN,所以BN=AM=$\frac{1}{4}$AB,所以MN=$\frac{1}{2}$AB,即$\frac{MN}{AB}$=$\frac{1}{2}$.
A M N B(图略)
当点N在线段AB 的延长线上时,如图2,因为AN-BN=MN,AN-BN=AB,所以MN=AB,即$\frac{MN}{AB}$=1.
A M B N(图略)综上所述,$\frac{MN}{AB}$的值为$\frac{1}{2}$或1.A M N B图1
A M B N图2
13 运算能力[2025合肥期末]如图,线段$AB= 1$,点$A_{1}$是线段AB的中点,点$A_{2}是线段A_{1}B$的中点,点$A_{3}是线段A_{2}B$的中点……以此类推,点$A_{n+1}是线段A_{n}B$的中点.
(1)线段$A_{3}B$的长为____;
(2)线段$A_{n}B$的长为____;
(3)$AA_{1}+A_{1}A_{2}+A_{2}A_{3}+... +A_{6}A_{7}$的值为____.
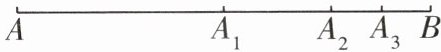
(1)线段$A_{3}B$的长为____;
(2)线段$A_{n}B$的长为____;
(3)$AA_{1}+A_{1}A_{2}+A_{2}A_{3}+... +A_{6}A_{7}$的值为____.
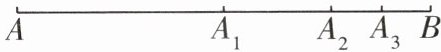
答案:
(1)$(\frac{1}{2})^{3}$;
(2)$(\frac{1}{2})^{n}$;
(3)${1}-(\frac{1}{2})^{7}$(图略) (图略) (图略)
(图略)
(1)由线段中点的定义可知,$A_{1}B=\frac{1}{{2}}AB=\frac{1}{2}$,$A_{2}B=\frac{1}{2}A_{{1}}B=\frac{1}{{{2}}}×\frac{1}{2}AB=(\frac{1}{2})^{2}$,$A_{3}B=\frac{1}{2}A_{2}B=\frac{1}{2}×\frac{1}{{2}}×\frac{1}{2}AB=(\frac{1}{2})^{3}$.
(2)由
(1)可推断$A_{n}B=(\frac{1}{2})^{n}AB=(\frac{1}{2})^{n}$.
(3)由
(2)可知,$A_{7}B=(\frac{1}{2})^{7}$,所以$AA_{1}+A_{1}A_{2}+A_{2}A_{3}+\cdots+A_{6}A_{7}=AB-A_{7}B=1-(\frac{1}{2})^{7}$.
(1)$(\frac{1}{2})^{3}$;
(2)$(\frac{1}{2})^{n}$;
(3)${1}-(\frac{1}{2})^{7}$(图略) (图略) (图略)
(图略)
(1)由线段中点的定义可知,$A_{1}B=\frac{1}{{2}}AB=\frac{1}{2}$,$A_{2}B=\frac{1}{2}A_{{1}}B=\frac{1}{{{2}}}×\frac{1}{2}AB=(\frac{1}{2})^{2}$,$A_{3}B=\frac{1}{2}A_{2}B=\frac{1}{2}×\frac{1}{{2}}×\frac{1}{2}AB=(\frac{1}{2})^{3}$.
(2)由
(1)可推断$A_{n}B=(\frac{1}{2})^{n}AB=(\frac{1}{2})^{n}$.
(3)由
(2)可知,$A_{7}B=(\frac{1}{2})^{7}$,所以$AA_{1}+A_{1}A_{2}+A_{2}A_{3}+\cdots+A_{6}A_{7}=AB-A_{7}B=1-(\frac{1}{2})^{7}$.
如图,点C,D是线段AB上两点(点C在点D的左侧),$AB= 4cm$.

(1)若$AD= 1.5cm,BC= 3.5cm$,则CD的长度为____;
(2)若点D是线段AB的中点,点C是线段AD的中点,则CD的长度为____;
(3)若$AC:BC= 1:4,AD:BD= 2:3$,则CD的长度为____;
(4)若点D是线段AB的三等分点,点C是线段AD的中点,则CD的长度为____;
(5)若$AC= BD$,延长线段BA到点M,使$MD= 5cm$,点N是线段CM的中点,则AN的长度为____.

(1)若$AD= 1.5cm,BC= 3.5cm$,则CD的长度为____;
(2)若点D是线段AB的中点,点C是线段AD的中点,则CD的长度为____;
(3)若$AC:BC= 1:4,AD:BD= 2:3$,则CD的长度为____;
(4)若点D是线段AB的三等分点,点C是线段AD的中点,则CD的长度为____;
(5)若$AC= BD$,延长线段BA到点M,使$MD= 5cm$,点N是线段CM的中点,则AN的长度为____.
答案:
解:
(1)1 cm
因为AB=4 cm,AD=1.5 cm,所以BD=AB-AD=2.5 cm,所以CD=BC-BD=3.5-2.5=1(cm).\\
(2)1 cm
因为点D是线段AB的中点,所以AD=$\frac{1}{2}$AB=2 cm,因为点C是线段AD的中点,所以CD=$\frac{1}{2}$AD=1 cm.\\
(3)$\frac{4}{5}$ cm
因为AC:BC=1:4,AD:BD=2:3,所以AC=$\frac{1}{5}$AB=$\frac{4}{5}$ cm,AD=$\frac{2}{5}$AB=$\frac{8}{5}$ cm,所以CD=AD-AC=$\frac{4}{5}$ cm.\\
(4)$\frac{2}{3}$ cm或$\frac{4}{3}$ cm
因为点C是线段AD的中点,所以CD=$\frac{1}{2}$AD.分情况讨论:当点D靠近点A时,因为点D是线段AB的三等分点,所以AD=$\frac{1}{3}$AB=$\frac{4}{3}$ cm,所以CD=$\frac{1}{2}×\frac{4}{3}=\frac{2}{3}$(cm);当点D靠近点B时,因为点D是线段AB的三等分点,所以AD=$\frac{2}{3}$AB=$\frac{8}{3}$ cm,所以CD=$\frac{1}{2}×\frac{8}{3}=\frac{4}{3}$(cm).故CD的长度为$\frac{2}{3}$ cm或$\frac{4}{3}$ cm.\\
(5)$\frac{1}{2}$ cm
设AC=BD=x,则AM=BM-AB=5+x-4=(1+x)cm,所以MC=AM+AC=(2x+1)cm.因为点N是线段CM的中点,所以CN=$\frac{1}{2}$CM=($\frac{1}{2}$+x)cm,所以AN=CN-AC=$\frac{1}{2}$ cm.
(1)1 cm
因为AB=4 cm,AD=1.5 cm,所以BD=AB-AD=2.5 cm,所以CD=BC-BD=3.5-2.5=1(cm).\\
(2)1 cm
因为点D是线段AB的中点,所以AD=$\frac{1}{2}$AB=2 cm,因为点C是线段AD的中点,所以CD=$\frac{1}{2}$AD=1 cm.\\
(3)$\frac{4}{5}$ cm
因为AC:BC=1:4,AD:BD=2:3,所以AC=$\frac{1}{5}$AB=$\frac{4}{5}$ cm,AD=$\frac{2}{5}$AB=$\frac{8}{5}$ cm,所以CD=AD-AC=$\frac{4}{5}$ cm.\\
(4)$\frac{2}{3}$ cm或$\frac{4}{3}$ cm
因为点C是线段AD的中点,所以CD=$\frac{1}{2}$AD.分情况讨论:当点D靠近点A时,因为点D是线段AB的三等分点,所以AD=$\frac{1}{3}$AB=$\frac{4}{3}$ cm,所以CD=$\frac{1}{2}×\frac{4}{3}=\frac{2}{3}$(cm);当点D靠近点B时,因为点D是线段AB的三等分点,所以AD=$\frac{2}{3}$AB=$\frac{8}{3}$ cm,所以CD=$\frac{1}{2}×\frac{8}{3}=\frac{4}{3}$(cm).故CD的长度为$\frac{2}{3}$ cm或$\frac{4}{3}$ cm.\\
(5)$\frac{1}{2}$ cm
设AC=BD=x,则AM=BM-AB=5+x-4=(1+x)cm,所以MC=AM+AC=(2x+1)cm.因为点N是线段CM的中点,所以CN=$\frac{1}{2}$CM=($\frac{1}{2}$+x)cm,所以AN=CN-AC=$\frac{1}{2}$ cm.
查看更多完整答案,请扫码查看


