第9页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1 [2025 黑龙江大庆校级期中]如图,有一个直角三角形纸板破损了一个角,如果把它补成完整的三角形纸板,需要补的角的度数是 (
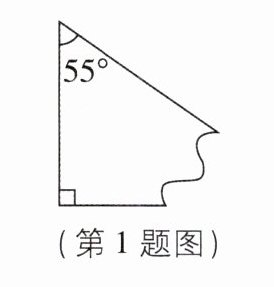
A.$45^{\circ}$
B.$35^{\circ}$
C.$55^{\circ}$
D.$25^{\circ}$
B
)
A.$45^{\circ}$
B.$35^{\circ}$
C.$55^{\circ}$
D.$25^{\circ}$
答案:
B 【解析】
∵ 直角三角形的两锐角互余,
∴ 需要补的角的度数为$90^{\circ }-55^{\circ }=35^{\circ }$,故选 B.
∵ 直角三角形的两锐角互余,
∴ 需要补的角的度数为$90^{\circ }-55^{\circ }=35^{\circ }$,故选 B.
在 $Rt\triangle ABC$ 中, $\angle C = 90^{\circ}$, $\angle A = 2\angle B$,则 $\angle A = $ (
A.$60^{\circ}$
B.$30^{\circ}$
C.$45^{\circ}$
D.$90^{\circ}$
A
)A.$60^{\circ}$
B.$30^{\circ}$
C.$45^{\circ}$
D.$90^{\circ}$
答案:
A 【解析】在$\text{Rt}\triangle ABC$中,$∠C=90^{\circ }$,
∴$∠A+∠B=90^{\circ }$.$\because$$∠A=2∠B$,
∴$3∠B=90^{\circ }$,$\therefore$$∠B=30^{\circ }$,$\therefore$$∠A=60^{\circ }$.故选 A.
∴$∠A+∠B=90^{\circ }$.$\because$$∠A=2∠B$,
∴$3∠B=90^{\circ }$,$\therefore$$∠B=30^{\circ }$,$\therefore$$∠A=60^{\circ }$.故选 A.
如图,在直角三角形 $ABC$ 中, $\angle BAC = 90^{\circ}$, $AC \neq AB$, $DE \perp AC$, $DF \perp AB$, $AD \perp BC$,则图中与 $\angle C$ ( $\angle C$ 除外)相等的角的个数是 (
A.3 个
B.4 个
C.5 个
D.6 个
A
)A.3 个
B.4 个
C.5 个
D.6 个
答案:
A 【解析】$\because$$∠BAC=90^{\circ }$,$AD⊥BC$,$DF⊥AB$,$\therefore$$∠C+∠B=90^{\circ }$,$∠BAD+∠B=90^{\circ }$,$∠BDF+∠B=90^{\circ }$,$\therefore$$∠C=∠BDF=∠BAD$.同理,$∠DAC+∠C=90^{\circ }$,$∠DAC+∠ADE=90^{\circ }$,$\therefore$$∠C=∠ADE$,$\therefore$题图中与$∠C$($∠C$除外)相等的角的个数是 3 个,故选 A.
4 如图,小明在计算机上用“几何画板”画了一个 $Rt\triangle ABC$, $\angle C = 90^{\circ}$,并画出了两锐角的平分线 $AD$, $BE$ 及其交点 $F$. 小明发现,无论怎样变动 $Rt\triangle ABC$ 的形状和大小, $\angle AFB$ 的度数是定值. 这个定值为
$135^{\circ }$
.
答案:
$135^{\circ }$【解析】$\because$$∠C=90^{\circ }$,$\therefore$$∠CAB+∠CBA=90^{\circ }$.$\because$AD 平分$∠CAB$,BE 平分$∠ABC$,$\therefore$$∠FAB=\frac {1}{2}∠CAB$,$∠FBA=\frac {1}{2}∠CBA$,$\therefore$$∠FAB+∠FBA=\frac {1}{2}(∠CAB+∠CBA)=45^{\circ }$,$\therefore$$∠AFB=180^{\circ }-45^{\circ }=135^{\circ }$.故答案为$135^{\circ }$.
5 [2025 辽宁鞍山质检]如图, $\triangle ABC$ 是直角三角形, $\angle C = 90^{\circ}$, $\angle A = 30^{\circ}$,过 $AB$ 边上一点 $D$ 剪下 $\triangle ADE$,点 $E$ 在 $AC$ 上,当 $\triangle ADE$ 是直角三角形时, $\angle AED$ 的度数是______.
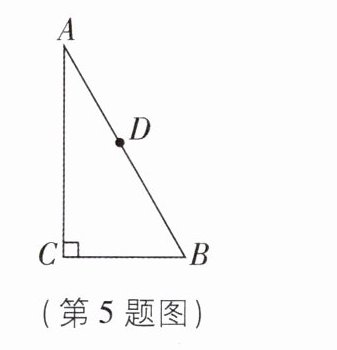

答案:
$60^{\circ }$或$90^{\circ }$【解析】当点 D 为直角顶点时,如图(1)所示,则$∠ADE=90^{\circ }$.$\because$$∠A=30^{\circ }$,$\therefore$$∠AED=90^{\circ }-30^{\circ }=60^{\circ }$.

思路分析
分两种情况讨论:点 D 为直角顶点;点 E 为直角顶点.
易错警示
没有确定三角形最大内角的情况下,应分类讨论作答,本题可分为以下两种情况:①$∠C=90^{\circ }$;②$∠B=90^{\circ }$.注意不要漏解.
当点 E 为直角顶点时,如图(2)所示,则$∠AED=90^{\circ }$.综上,$∠AED$的度数为$60^{\circ }$或$90^{\circ }$.

$60^{\circ }$或$90^{\circ }$【解析】当点 D 为直角顶点时,如图(1)所示,则$∠ADE=90^{\circ }$.$\because$$∠A=30^{\circ }$,$\therefore$$∠AED=90^{\circ }-30^{\circ }=60^{\circ }$.

思路分析
分两种情况讨论:点 D 为直角顶点;点 E 为直角顶点.
易错警示
没有确定三角形最大内角的情况下,应分类讨论作答,本题可分为以下两种情况:①$∠C=90^{\circ }$;②$∠B=90^{\circ }$.注意不要漏解.
当点 E 为直角顶点时,如图(2)所示,则$∠AED=90^{\circ }$.综上,$∠AED$的度数为$60^{\circ }$或$90^{\circ }$.

6 [2024 陕西汉中期末]如图,在 $\triangle ABC$ 中, $\angle BAC = 90^{\circ}$, $BD$ 平分 $\angle ABC$.
(1)若 $\angle C = 40^{\circ}$,求 $\angle ADB$ 的度数.
(2)在图中画出 $\triangle ABC$ 的边 $BC$ 上的高 $AE$,与 $BD$ 交于点 $F$. 试说明:① $\angle BAE = \angle C$;② $\angle AFD = \angle ADF$.
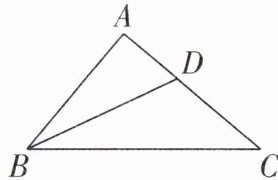
(1)若 $\angle C = 40^{\circ}$,求 $\angle ADB$ 的度数.
(2)在图中画出 $\triangle ABC$ 的边 $BC$ 上的高 $AE$,与 $BD$ 交于点 $F$. 试说明:① $\angle BAE = \angle C$;② $\angle AFD = \angle ADF$.

答案:
【解】(1)在$\triangle ABC$中,$∠BAC=90^{\circ }$,$∠C=40^{\circ }$,$\therefore$$∠ABC=90^{\circ }-40^{\circ }=50^{\circ }$.$\because$BD 平分$∠ABC$,$\therefore$$∠ABD=∠DBC=\frac {1}{2}∠ABC=25^{\circ }$,$\therefore$$∠ADB=90^{\circ }-∠ABD=65^{\circ }$.
(2)如图所示.①$\because$AE 是 BC 边上的高线,

$\therefore$$∠AEC=90^{\circ }$,$\therefore$$∠C+∠CAE=90^{\circ }$.$\because$$∠BAC=90^{\circ }$,$\therefore$$∠BAE+∠CAE=90^{\circ }$,$\therefore$$∠BAE=∠C$.②$\because$AE 是 BC 边上的高线,$\therefore$$∠AEB=90^{\circ }$,$\therefore$$∠DBC+∠BFE=90^{\circ }$.$\because$$∠BFE=∠AFD$,$∠ABD=∠DBC$,$\therefore$$∠AFD+∠ABD=90^{\circ }$.$\because$$∠ABD+∠ADF=90^{\circ }$,$\therefore$$∠AFD=∠ADF$.
【解】(1)在$\triangle ABC$中,$∠BAC=90^{\circ }$,$∠C=40^{\circ }$,$\therefore$$∠ABC=90^{\circ }-40^{\circ }=50^{\circ }$.$\because$BD 平分$∠ABC$,$\therefore$$∠ABD=∠DBC=\frac {1}{2}∠ABC=25^{\circ }$,$\therefore$$∠ADB=90^{\circ }-∠ABD=65^{\circ }$.
(2)如图所示.①$\because$AE 是 BC 边上的高线,

$\therefore$$∠AEC=90^{\circ }$,$\therefore$$∠C+∠CAE=90^{\circ }$.$\because$$∠BAC=90^{\circ }$,$\therefore$$∠BAE+∠CAE=90^{\circ }$,$\therefore$$∠BAE=∠C$.②$\because$AE 是 BC 边上的高线,$\therefore$$∠AEB=90^{\circ }$,$\therefore$$∠DBC+∠BFE=90^{\circ }$.$\because$$∠BFE=∠AFD$,$∠ABD=∠DBC$,$\therefore$$∠AFD+∠ABD=90^{\circ }$.$\because$$∠ABD+∠ADF=90^{\circ }$,$\therefore$$∠AFD=∠ADF$.
7 [2025 浙江宁波质检]如图,在 $Rt\triangle ABC$ 中, $\angle B = 90^{\circ}$,直线 $DE$ 与 $AC$, $BC$ 分别交于 $D$, $E$ 两点. 若 $\angle DEC = \angle A$,则 $\triangle EDC$ 是 (
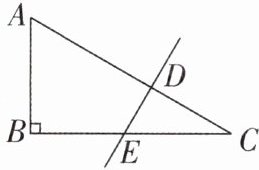
A.锐角三角形
B.直角三角形
C.钝角三角形
D.无法判断
B
)
A.锐角三角形
B.直角三角形
C.钝角三角形
D.无法判断
答案:
B 【解析】在$\text{Rt}\triangle ABC$中,$∠B=90^{\circ }$,$\therefore$$∠A+∠C=90^{\circ }$.$\because$$∠DEC=∠A$,$\therefore$$∠DEC+∠C=90^{\circ }$,$\therefore$$\triangle EDC$是直角三角形.故选 B.
8 [2024 福建莆田校级调研]如图, $CE \perp AD$,垂足为 $E$, $\angle A = \angle C$. 求证: $\triangle ABD$ 是直角三角形.
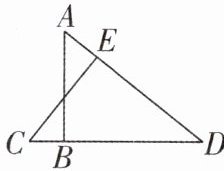

答案:
【证明】$\because$$CE⊥AD$,$\therefore$$∠CED=90^{\circ }$,$\therefore$$∠C+∠D=90^{\circ }$.$\because$$∠A=∠C$,$\therefore$$∠A+∠D=90^{\circ }$,$\therefore$$∠ABD=90^{\circ }$,$\therefore$$\triangle ABD$是直角三角形.
在直角三角形 $ABC$ 中, $\angle A : \angle B : \angle C = 1 : m : 3$,则 $m$ 的值是______
2 或 4
.
答案:
2 或 4 【解析】设$∠A=x^{\circ }$,$∠C=3x^{\circ }$.当$∠C=90^{\circ }$时,$3x^{\circ }=90^{\circ }$,解得$x=30$,$\therefore$$∠A=30^{\circ }$,$∠B=90^{\circ }-30^{\circ }=60^{\circ }$,$\therefore$$∠A:∠B:∠C=1:2:3$,$\therefore$$m=2$;当$∠B=90^{\circ }$时,$∠A+∠C=90^{\circ }$,即$x^{\circ }+3x^{\circ }=90^{\circ }$,解得$x=22.5$,$\therefore$$∠A=22.5^{\circ }$,$∠C=67.5^{\circ }$,$\therefore$$∠A:∠B:∠C=1:4:3$,$\therefore$$m=4$,故 m 的值是 2 或 4.
查看更多完整答案,请扫码查看


