第49页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1[2024山东济宁期中]若等腰三角形的一个角等于$80^{\circ }$,则它的其余两个角的度数为(
A.$80^{\circ },20^{\circ }$
B.$50^{\circ },50^{\circ }$
C.$80^{\circ },20^{\circ }或50^{\circ },50^{\circ }$
D.$30^{\circ },70^{\circ }或10^{\circ },90^{\circ }$
C
)A.$80^{\circ },20^{\circ }$
B.$50^{\circ },50^{\circ }$
C.$80^{\circ },20^{\circ }或50^{\circ },50^{\circ }$
D.$30^{\circ },70^{\circ }或10^{\circ },90^{\circ }$
答案:
C [解析]①当80°的角是顶角时,两个底角的度数为50°,50°;②当80°的角是底角时,顶角的度数为20°.故它的其余两个角的度数为50°,50°或80°,20°.故选C.
如图,已知O是四边形ABCD内一点,$OA= OB= OC,∠ABC= ∠ADC= 70^{\circ }$,则$∠DAO+∠DCO$的大小是(
A.$70^{\circ }$
B.$110^{\circ }$
C.$140^{\circ }$
D.$150^{\circ }$
D
)A.$70^{\circ }$
B.$110^{\circ }$
C.$140^{\circ }$
D.$150^{\circ }$
答案:
D [解析]
∵OA=OB=OC,∠ABC=∠ADC=70°,
∴∠ABO=∠BAO,∠OBC=∠OCB,
∴∠AOB+∠BOC=360°−2(∠ABO+∠OBC)=220°,
∴∠AOC=360°−220°=140°.
∵∠OAD+∠ADC+∠OCD+∠AOC=360°,
∴∠DAO+∠DCO=150°.故选D.
∵OA=OB=OC,∠ABC=∠ADC=70°,
∴∠ABO=∠BAO,∠OBC=∠OCB,
∴∠AOB+∠BOC=360°−2(∠ABO+∠OBC)=220°,
∴∠AOC=360°−220°=140°.
∵∠OAD+∠ADC+∠OCD+∠AOC=360°,
∴∠DAO+∠DCO=150°.故选D.
3[2024江苏常州新北区期中]如图,在$\triangle ABC$中,$∠ABC= 40^{\circ },∠BAC= 80^{\circ }$,以点A为圆心,AC长为半径作弧,交射线BA于点D,连接CD,则$∠BCD$的度数是( )

A.$10^{\circ }$
B.$120^{\circ }$
C.$10^{\circ }或100^{\circ }$
D.$60^{\circ }或120^{\circ }$

A.$10^{\circ }$
B.$120^{\circ }$
C.$10^{\circ }或100^{\circ }$
D.$60^{\circ }或120^{\circ }$
答案:
C [解析]如图.在△ABC中,∠ABC=40°, ∠BAC=80°,
∠BAC=80°,
∴∠ACB=180°−40°−80°=60°.①由作图可知AC=AD,
∴∠ACD=∠ADC=$\frac{1}{2}$×(180°−80°)=50°,
∴∠BCD=∠ACB−∠ACD=60°−50°=10°;②由作图可知AC=AD',
∴∠ACD'=∠AD'C.
∵∠ACD'+∠AD'C=∠BAC=80°,
∴∠AD'C=40°,
∴∠BCD'=180°−∠ABC−∠AD'C=180°−40°−40°=100°.综上所述,∠BCD的度数是10°或100°.故选C.
C [解析]如图.在△ABC中,∠ABC=40°,
 ∠BAC=80°,
∠BAC=80°,∴∠ACB=180°−40°−80°=60°.①由作图可知AC=AD,
∴∠ACD=∠ADC=$\frac{1}{2}$×(180°−80°)=50°,
∴∠BCD=∠ACB−∠ACD=60°−50°=10°;②由作图可知AC=AD',
∴∠ACD'=∠AD'C.
∵∠ACD'+∠AD'C=∠BAC=80°,
∴∠AD'C=40°,
∴∠BCD'=180°−∠ABC−∠AD'C=180°−40°−40°=100°.综上所述,∠BCD的度数是10°或100°.故选C.
4如图,在第一个三角形$A_{1}BC$中,$∠B= 30^{\circ },A_{1}B= CB$,在边$A_{1}B$上任取一点D,延长$CA_{1}到A_{2}$,使$A_{1}A_{2}= A_{1}D$,得到第二个三角形$A_{1}A_{2}D$,在边$A_{2}D$上任取一点E,延长$A_{1}A_{2}到A_{3}$,使$A_{2}A_{3}= A_{2}E$,得到第三个三角形$A_{2}A_{3}E$,…,按此作法继续下去,第n个等腰三角形的底角的度数是______$^{\circ }$.(n为正整数)
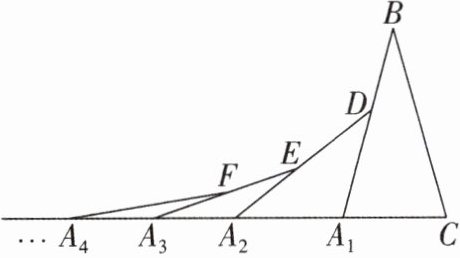

$\frac{75}{2^{n-1}}$
答案:
$(\frac{75}{2^{n-1}})$ [解析]
∵在△CBA₁中,∠B=30°,CB=A₁B,
∴∠BA₁C=$\frac{180°-∠B}{2}$=75°.
∵A₁A₂=A₁D,∠BA₁C是△A₁A₂D的外角,
∴∠DA₂A₁=$\frac{1}{2}$∠BA₁C=$\frac{1}{2}$×75°=37.5°.同理可得,∠EA₃A₂=$(\frac{75}{4})°$,∠FA₄A₃=$(\frac{75}{8})°$,
∴第n个等腰三角形的底角的度数是$(\frac{75}{2^{n-1}})°$.
∵在△CBA₁中,∠B=30°,CB=A₁B,
∴∠BA₁C=$\frac{180°-∠B}{2}$=75°.
∵A₁A₂=A₁D,∠BA₁C是△A₁A₂D的外角,
∴∠DA₂A₁=$\frac{1}{2}$∠BA₁C=$\frac{1}{2}$×75°=37.5°.同理可得,∠EA₃A₂=$(\frac{75}{4})°$,∠FA₄A₃=$(\frac{75}{8})°$,
∴第n个等腰三角形的底角的度数是$(\frac{75}{2^{n-1}})°$.
5如图,在$\triangle ABC$中,$AB= AC,AD⊥BC$于点D,$DE⊥AB$于点E,$DF⊥AC$于点F,下列结论:①$∠BAD= ∠CAD$;②AD上任意一点到AB,AC的距离相等;③$BD= CD$;④若点P在直线AD上,则$PB= PC$.其中正确的是(

A.①
B.①②
C.①②③
D.①②③④
D
)
A.①
B.①②
C.①②③
D.①②③④
答案:
D [解析]
∵AB=AC,AD⊥BC于点D,
∴AD平分∠BAC,即∠BAD=∠CAD,BD=CD,①③正确;
∵AD平分∠BAC,
∴AD上任意一点到AB,AC的距离相等,②正确;
∵AD⊥BC,BD=CD,
∴AD为BC的垂直平分线.
∵点P在直线AD上,
∴PB=PC,④正确.故选D.
∵AB=AC,AD⊥BC于点D,
∴AD平分∠BAC,即∠BAD=∠CAD,BD=CD,①③正确;
∵AD平分∠BAC,
∴AD上任意一点到AB,AC的距离相等,②正确;
∵AD⊥BC,BD=CD,
∴AD为BC的垂直平分线.
∵点P在直线AD上,
∴PB=PC,④正确.故选D.
如图,在平面直角坐标系xOy中,$\triangle ABC$为等腰三角形,$AB= AC,BC// x$轴,若点$A(2,5),B(-1,1)$,则点C的坐标为(
A.$(2,3)$
B.$(3,1)$
C.$(5,1)$
D.$(1,5)$
C
)A.$(2,3)$
B.$(3,1)$
C.$(5,1)$
D.$(1,5)$
答案:
C [解析]过点A作AD⊥BC于D,如图.
∵AB=AC,AD⊥BC,
∴BD=CD.
∵点A(2,5),B(−1,1),BC//x轴,
∴点D(2,1).设点C(m,1),则CD=m−2.
∵BD=2−(−1)=3,
∴m−2=3,
∴m=5,
∴点C的坐标为(5,1),故选C.
∵AB=AC,AD⊥BC,
∴BD=CD.
∵点A(2,5),B(−1,1),BC//x轴,
∴点D(2,1).设点C(m,1),则CD=m−2.
∵BD=2−(−1)=3,
∴m−2=3,
∴m=5,
∴点C的坐标为(5,1),故选C.
7[2024黑龙江哈尔滨质检]如图,$AC= AB= BD,∠ABD= 90^{\circ },BC= 6$,则$\triangle BCD$的面积为______.


答案:
9 [解析]如图,作AE⊥BC于E,作DF⊥CB交CB的延长线于F.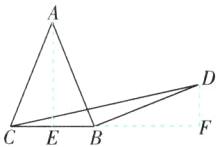
∵AB=AC,BC=6,
∴CE=BE=$\frac{1}{2}$BC=3.
∵∠ABD=90°,DF⊥CB,
∴∠ABC+∠DBF=∠BDF+∠DBF,
∴∠ABC=∠BDF.
∵AE⊥BC,
∴∠AEB=∠BFD=90°.在△ABE和△BDF中,$\left\{\begin{array}{l} ∠ABC=∠BDF,\\ ∠AEB=∠BFD,\\ AB=BD,\end{array}\right. $
∴△ABE≌△BDF(AAS),
∴DF=BE=3,
∴S△BCD=$\frac{1}{2}$BC·DF=$\frac{1}{2}$×6×3=9.故答案为9.
9 [解析]如图,作AE⊥BC于E,作DF⊥CB交CB的延长线于F.

∵AB=AC,BC=6,
∴CE=BE=$\frac{1}{2}$BC=3.
∵∠ABD=90°,DF⊥CB,
∴∠ABC+∠DBF=∠BDF+∠DBF,
∴∠ABC=∠BDF.
∵AE⊥BC,
∴∠AEB=∠BFD=90°.在△ABE和△BDF中,$\left\{\begin{array}{l} ∠ABC=∠BDF,\\ ∠AEB=∠BFD,\\ AB=BD,\end{array}\right. $
∴△ABE≌△BDF(AAS),
∴DF=BE=3,
∴S△BCD=$\frac{1}{2}$BC·DF=$\frac{1}{2}$×6×3=9.故答案为9.
8如图,$\triangle ABC$是等腰三角形,$AB= AC,∠A= 20^{\circ }$,BP平分$∠ABC$,点D是射线BP上一点,如果点D满 足$\triangle BCD$是等腰三角形,那么$∠BDC$的度数是______.
足$\triangle BCD$是等腰三角形,那么$∠BDC$的度数是______.
 足$\triangle BCD$是等腰三角形,那么$∠BDC$的度数是______.
足$\triangle BCD$是等腰三角形,那么$∠BDC$的度数是______.
答案:
40°或70°或100° [解析]①当BC=CD时,如图
(1)所示.
∵∠A=20°,AB=AC,
∴∠ABC=80°.
∵BP平分∠ABC,
∴∠CBD=40°.
∵BC=CD,
∴∠CBD=∠BDC=40°.②当BD=BC时,如图
(2)所示. 由①可知∠CBD=40°.
由①可知∠CBD=40°.
∵BD=BC,
∴∠BDC=70°.③当DB=DC时,如图
(3)所示. 由①可知∠CBD=40°.
由①可知∠CBD=40°.
∵BD=CD,
∴∠BDC=100°.故答案为40°或70°或100°.
40°或70°或100° [解析]①当BC=CD时,如图
(1)所示.

∵∠A=20°,AB=AC,
∴∠ABC=80°.
∵BP平分∠ABC,
∴∠CBD=40°.
∵BC=CD,
∴∠CBD=∠BDC=40°.②当BD=BC时,如图
(2)所示.
 由①可知∠CBD=40°.
由①可知∠CBD=40°.∵BD=BC,
∴∠BDC=70°.③当DB=DC时,如图
(3)所示.
 由①可知∠CBD=40°.
由①可知∠CBD=40°.∵BD=CD,
∴∠BDC=100°.故答案为40°或70°或100°.
查看更多完整答案,请扫码查看


