《2025年初中必刷题八年级数学上册人教版》

一个零件的形状如图所示,按照规定,AB所在直线和CD所在直线的夹角为40°的零件为合格零件.要检验该零件是否合格,有以下三种方案:
甲:延长BA和CD,设交点为O,然后测量∠O是否等于40°就可以检验该零件是否合格;
乙:只需测量出∠B和∠C的度数;
丙:测量出∠BAD和∠ADC的度数也可以检验该零件是否合格.
则正确的方案有(A)
A.甲、乙、丙
B.甲、乙
C.甲、丙
D.乙、丙

答案： A　[解析]甲:延长BA和CD,设交点为O,则测量∠O是否等于40°可以检验该零件是否合格,符合题意;乙:只需测量出∠B和∠C的度数,由三角形内角和定理即可检验该零件是否合格,符合题意;丙:测量出∠BAD和∠ADC的度数,利用邻补角的定义和三角形内角和定理即可检验该零件是否合格,符合题意.故选A.

三角形中,如果一个角是另一个角的3倍,这样的三角形我们称之为“灵动三角形”.例如,三个内角分别为120°,40°,20°的三角形是“灵动三角形”.如图,∠MON= 60°,在射线OM上找一点A,过点A作AB⊥OM交ON于点B,以A为端点作射线AD,交线段OB于点C(0°＜∠OAC＜90°).

①∠ABO的度数为30°;
②△AOB是“灵动三角形”;
③若∠BAC= 70°,则△AOC是“灵动三角形”;
④当△ABC为“灵动三角形”时,∠OAC的度数为30°或52.5°.
正确的结论有(C)
A.1个
B.2个
C.3个
D.4个

答案： C　[解析]
∵AB⊥OM,
∴∠BAO=90°.
∵∠AOB=60°,
∴∠ABO=90°−60°=30°.
∵90°=3×30°,
∴△AOB是“灵动三角形”，故①②正确.
∵∠OAB=90°,∠BAC=70°,
∴∠OAC=20°.
∵∠AOC=60°=3×20°,
∴△AOC是“灵动三角形”,故③正确.
∵△ABC是“灵动三角形”，分三种情况讨论:当∠ACB=3∠ABC时,∠ACB=90°,
∴∠CAB=60°,
∴∠OAC=30°;当∠ABC=3∠CAB时,∠CAB=10°,
∴∠OAC=80°;当∠ACB=3∠CAB时,
∵∠CAB+∠ACB+∠ABC=180°,即4∠CAB+30°=180°,
∴∠CAB=37.5°,
∴∠OAC=52.5°.综上所述,满足条件的∠OAC的度数为30°或52.5°或80°,故④错误.综上所述,正确的有①②③,共3个.故选C.

3[2024江苏宿迁宿城区期末,较难]如图,在△ABC中,∠ABC= 50°,∠ACB= 100°,M是射线AB上的一个动点,过点M作MN//BC交射线AC于点N,连接BN,若△BMN中有两个角相等,则∠MNB的度数为____.

答案：
25°或50°或65°或80°　[解析]
(1)当点M在线段AB上时,如图
(1).
∵MN//BC,
∴∠ABC=∠AMN=50°,
∴∠BMN=180°−50°=130°.
∵△BMN中有两个角相等,
∴只有∠MBN=∠BNM这一种情况,
∴∠MNB=$\frac{180°−130°}{2}$=25°.

(2)当点M在AB的延长线上时,如图
(2).①当∠BMN=∠BNM时,由MN//BC,得∠BMN=∠ABC=50°,
∴∠BNM=50°.②当∠BMN=∠MBN时,∠BMN=∠ABC=50°,
∴∠MBN=50°,
∴∠MNB=180°−50°−50°=80°.③当∠MBN=∠MNB时,∠BMN=∠ABC=50°,
∴∠MNB=$\frac{180°−50°}{2}$=65°.综上所述,∠MNB的度数为25°或50°或65°或80°,故答案为25°或50°或65°或80°.

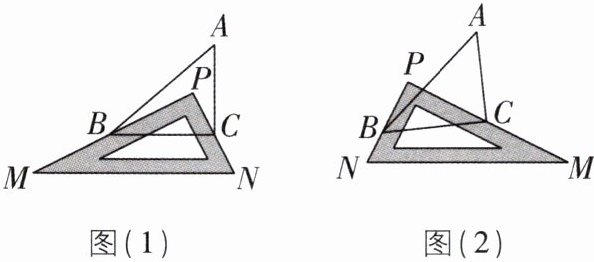
4核心素养推理能力[2024辽宁抚顺期中,中]将三角尺(△MPN,∠MPN= 90°)放置在△ABC上(点P在△ABC内),如图(1)所示,三角尺的两边PM,PN恰好经过点B和点C.探究∠ABP与∠ACP是否存在某种数量关系.
(1)特例探索:若∠A= 50°,则∠PBC+∠PCB= ____°,∠ABP+∠ACP= ____°;
(2)类比探索:写出∠ABP,∠ACP,∠A之间满足的数量关系,并说明理由;
(3)变式探索:如图(2),改变三角尺的位置,使点P在△ABC外,三角尺的两边PM,PN恰好经过点C和点B,写出∠ABP,∠ACP,∠A之间满足的数量关系,并说明理由.

答案：
[解]
(1)
∵∠A=50°,
∴∠ABC+∠ACB=130°.
∵∠P=90°,
∴∠PBC+∠PCB=90°,
∴∠ABP+∠ACP=130°−90°=40°,故答案为90,40.
(2)∠ABP+∠ACP=90°-∠A.理由:
∵(∠PBC+∠PCB)+(∠ABP+∠ACP)+∠A=180°,
∴(180°-∠P)+(∠ABP+∠ACP)+∠A=180°.
∵∠P=90°,
∴∠ABP+∠ACP+∠A=90°,
∴∠ABP+∠ACP=90°-∠A.
(3)∠ACP-∠ABP=90°-∠A.理由:设AB交PC于O,如图.
∵∠AOC=∠POB,
∴∠ACO+∠A=∠P+∠PBO,即∠ACP+∠A=90°+∠ABP,
∴∠ACP-∠ABP=90°-∠A.