《2025年初中必刷题八年级数学上册人教版》

在$\triangle ABC$中,$AD为BC$边上的中线,若$\triangle ABD与\triangle ADC$的周长差为5,$AC= 8$,则$AB$的长为 (C)
A.2
B.13
C.3或13
D.2或12

答案： C　[解析]①当△ABD的周长大于△ADC的周长时，
∵AD为BC边上的中线,
∴BD=CD，
∴△ABD与△ADC的周长差=(AB+AD+BD)−(AC+AD+CD)=AB−AC.
∵△ABD与△ADC的周长差为5,AC=8,
∴AB−8=5,解得AB=13.②当△ADC的周长大于△ABD的周长时，
∵AD为BC边上的中线，
∴BD=CD,
∴△ADC与△ABD的周长差=(AC+AD+CD)−(AB+AD+BD)=AC−AB.
∵△ABD与△ADC的周长差为5,AC=8,
∴8−AB=5,解得AB=3.综上，AB=3或13,故选C.

在等腰三角形$ABC$中,$AB= AC$,若中线$BD$将该三角形的周长分为5和3两个部分,则该等腰三角形的底边长为 (A)
A.$\frac{4}{3}$
B.4
C.$\frac{4}{3}$或4
D.$\frac{5}{3}$或4

答案： 1. 设$AB = AC = 2x$，$BC=y$，因为$BD$是中线，所以$AD = CD=\frac{1}{2}AC = x$。
分两种情况讨论：
情况一：$\begin{cases}AB + AD=5\\BC + CD = 3\end{cases}$，即$\begin{cases}2x + x=5\\y + x = 3\end{cases}$。
解第一个方程$2x + x=5$：
根据合并同类项法则，$3x = 5$，解得$x=\frac{5}{3}$。
把$x = \frac{5}{3}$代入第二个方程$y+x = 3$：
则$y=3 - x$，$y = 3-\frac{5}{3}=\frac{9 - 5}{3}=\frac{4}{3}$。
此时三边长分别为$AB = AC=\frac{10}{3}$，$BC=\frac{4}{3}$。
检验三边关系：$\frac{10}{3}+\frac{10}{3}=\frac{20}{3}\gt\frac{4}{3}$，$\frac{10}{3}+\frac{4}{3}=\frac{14}{3}\gt\frac{10}{3}$，满足三角形三边关系（任意两边之和大于第三边）。
情况二：$\begin{cases}AB + AD=3\\BC + CD = 5\end{cases}$，即$\begin{cases}2x + x=3\\y + x = 5\end{cases}$。
解第一个方程$2x + x=3$：
根据合并同类项法则，$3x = 3$，解得$x = 1$。
把$x = 1$代入第二个方程$y + x=5$：
则$y=5 - x$，$y = 5 - 1=4$。
此时三边长分别为$AB = AC = 2$，$BC = 4$。
检验三边关系：$2 + 2=4$，不满足三角形三边关系（任意两边之和大于第三边），这种情况要舍去。
2. 综上：
该等腰三角形的底边长为$\frac{4}{3}$。
所以答案是A。

如图,$D,E,F分别是边BC$,$AD$,$AC$上的中点,若阴影部分的面积为6,则$\triangle ABC$的面积是 (D)
A.12
B.14
C.15
D.16

答案： 1. 首先，根据三角形中线的性质：
因为$D$是$BC$的中点，根据三角形中线将三角形分成面积相等的两部分，所以$S_{\triangle ABD}=S_{\triangle ACD}=\frac{1}{2}S_{\triangle ABC}$。
又因为$E$是$AD$的中点，所以$S_{\triangle BDE}=\frac{1}{2}S_{\triangle ABD}$，$S_{\triangle DEF}=\frac{1}{2}S_{\triangle ADF}$。
由于$F$是$AC$的中点，所以$S_{\triangle ADF}=\frac{1}{2}S_{\triangle ACD}$。
2. 然后，计算阴影部分面积与$\triangle ABC$面积的关系：
$S_{\triangle BDE}=\frac{1}{2}S_{\triangle ABD}=\frac{1}{2}×\frac{1}{2}S_{\triangle ABC}=\frac{1}{4}S_{\triangle ABC}$。
$S_{\triangle DEF}=\frac{1}{2}S_{\triangle ADF}$，而$S_{\triangle ADF}=\frac{1}{2}S_{\triangle ACD}=\frac{1}{2}×\frac{1}{2}S_{\triangle ABC}=\frac{1}{4}S_{\triangle ABC}$，所以$S_{\triangle DEF}=\frac{1}{2}×\frac{1}{4}S_{\triangle ABC}=\frac{1}{8}S_{\triangle ABC}$。
那么阴影部分面积$S = S_{\triangle BDE}+S_{\triangle DEF}$。
$S=\frac{1}{4}S_{\triangle ABC}+\frac{1}{8}S_{\triangle ABC}$。
通分可得$S=\frac{2 + 1}{8}S_{\triangle ABC}=\frac{3}{8}S_{\triangle ABC}$。
3. 最后，已知阴影部分面积$S = 6$：
由$\frac{3}{8}S_{\triangle ABC}=6$，根据等式的性质，$S_{\triangle ABC}=6÷\frac{3}{8}$。
根据除法运算法则$a÷\frac{b}{c}=a×\frac{c}{b}(b\neq0,c\neq0)$，则$S_{\triangle ABC}=6×\frac{8}{3}$。
$6×\frac{8}{3}=16$。
所以$\triangle ABC$的面积是$16$，答案是D。

如图,已知$\triangle ABC$的面积为1,分别倍长(延长一倍)边$AB$,$BC$,$CA$得到$\triangle A_{1}B_{1}C_{1}$,再分别倍长边$A_{1}B_{1}$,$B_{1}C_{1}$,$C_{1}A_{1}$得到$\triangle A_{2}B_{2}C_{2}$,…,按此规律,倍长2024次后得到的$\triangle A_{2024}B_{2024}C_{2024}$的面积为 (A)
A.$7^{2024}$
B.$5^{2024}$
C.$6^{2023}$
D.$4^{2023}$

答案： A　[解析]如图,连接AB₁,BC₁,CA₁,根据等底同高的三角形面积相等,可得△A₁BC,△A₁B₁C,△AB₁C,△AB₁C₁,△ABC₁,△A₁BC₁,△ABC的面积都相等,
∴S△A₁B₁C₁=7S△ABC,同理可得S△A₂B₂C₂=7S△A₁B₁C₁=7²S△ABC,…,则S△A₂₀₂₄B₂₀₂₄C₂₀₂₄=7²⁰²⁴S△ABC.
∵S△ABC=1,
∴△A₂₀₂₄B₂₀₂₄C₂₀₂₄的面积为7²⁰²⁴.故选A.

5 [2025江西景德镇质检,中]如图,$\triangle ABC的三条中线AD$,$BE$,$CF交于点G$.若$AG:GD= 2:1$,$S_{\triangle ABC}= 12$,则图中阴影部分的面积为______.

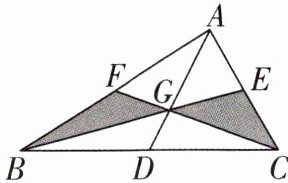
4

答案： 1. 首先，根据中线性质：
因为$AD$，$BE$，$CF$是$\triangle ABC$的中线，所以$S_{\triangle ABD}=S_{\triangle ACD}=\frac{1}{2}S_{\triangle ABC}$（三角形中线将三角形分成面积相等的两部分），已知$S_{\triangle ABC}=12$，则$S_{\triangle ABD}=S_{\triangle ACD}=\frac{1}{2}×12 = 6$。
又因为$AG:GD = 2:1$，且$\triangle ABG$与$\triangle BDG$的高相同（以$B$到$AD$的距离为高），根据三角形面积公式$S=\frac{1}{2}ah$（$a$为底，$h$为高），当高$h$相同时，面积比等于底之比。
对于$\triangle ABG$和$\triangle BDG$，$\frac{S_{\triangle ABG}}{S_{\triangle BDG}}=\frac{AG}{GD}$（$S_{\triangle ABG}=\frac{1}{2}AG\cdot h$，$S_{\triangle BDG}=\frac{1}{2}GD\cdot h$），因为$AG:GD = 2:1$，所以$S_{\triangle ABG}=\frac{2}{3}S_{\triangle ABD}$。
2. 然后，计算$S_{\triangle ABG}$的值：
把$S_{\triangle ABD}=6$代入$S_{\triangle ABG}=\frac{2}{3}S_{\triangle ABD}$，可得$S_{\triangle ABG}=\frac{2}{3}×6 = 4$，同理$S_{\triangle ACG}=\frac{2}{3}S_{\triangle ACD}=4$。
再根据$S_{\triangle AFG}=\frac{1}{2}S_{\triangle ABG}$（$F$是$AB$中点，$\triangle AFG$与$\triangle BFG$等底等高，$S_{\triangle AFG}=S_{\triangle BFG}$），所以$S_{\triangle AFG}=\frac{1}{2}×4 = 2$；同理$S_{\triangle CEG}=\frac{1}{2}S_{\triangle ACG}=2$。
3. 最后，求阴影部分面积：
阴影部分面积$S = S_{\triangle AFG}+S_{\triangle CEG}$。
所以$S=2 + 2=4$。
故答案为$4$。

(1)$S_{\triangle ABC}= \frac{1}{2}AC\cdot BC= $$\frac{1}{2}AB\cdot CD$.
(2)在(1)的条件下,若$AC= 3$,$BC= 4$,$AB= 5$,用等积法求$CD$的长.
由(1)可得$S_{\triangle ABC}=\frac{1}{2}AC\cdot BC=\frac{1}{2}AB\cdot CD$，则$\frac{1}{2}×3×4=\frac{1}{2}×5× CD$，解得$CD=\frac{12}{5}$
(3)如图(2),在等腰三角形$ABC$中,$AB= AC= 13$,$BC= 10$,过$A作AH\perp BC于点H$,且$AH= 12$,$P为底边BC$上的任意一点,过点$P作PM\perp AB$,$PN\perp AC$,垂足分别为$M$,$N$,连接$AP$,利用$S_{\triangle ABC}= S_{\triangle ABP}+S_{\triangle ACP}$,求$PM+PN$的值.
$\because AH\perp BC$，$PM\perp AB$，$PN\perp AC$，$S_{\triangle ABC}=S_{\triangle ABP}+S_{\triangle ACP}$，$\therefore \frac{1}{2}BC\cdot AH=\frac{1}{2}AB\cdot PM+\frac{1}{2}AC\cdot PN$，$\therefore \frac{1}{2}×10×12=\frac{1}{2}×13PM+\frac{1}{2}×13PN=\frac{1}{2}×13(PM+PN)$，$\therefore PM+PN=\frac{120}{13}$

答案：
(1)$\frac{1}{2}AB\cdot CD$
(2)由
(1)可得$S_{\triangle ABC}=\frac{1}{2}AC\cdot BC=\frac{1}{2}AB\cdot CD$，则$\frac{1}{2}×3×4=\frac{1}{2}×5× CD$，解得$CD=\frac{12}{5}$
(3)$\because AH\perp BC$，$PM\perp AB$，$PN\perp AC$，$S_{\triangle ABC}=S_{\triangle ABP}+S_{\triangle ACP}$，$\therefore \frac{1}{2}BC\cdot AH=\frac{1}{2}AB\cdot PM+\frac{1}{2}AC\cdot PN$，$\therefore \frac{1}{2}×10×12=\frac{1}{2}×13PM+\frac{1}{2}×13PN=\frac{1}{2}×13(PM+PN)$，$\therefore PM+PN=\frac{120}{13}$

已知$\triangle ABC$的面积为24,$AD是BC$边上的高(点$D不与点B$重合),若$AD= 4$,$CD= 5$,则$BD$的长为 (D)
A.1
B.1或11
C.7
D.7或17

答案： 1. 首先根据三角形面积公式$S = \frac{1}{2}ah$（$a$为底，$h$为高）：
已知$S_{\triangle ABC}=24$，$AD = 4$，设$BC$的长为$x$，则$S_{\triangle ABC}=\frac{1}{2}BC\cdot AD$。
把$S_{\triangle ABC}=24$，$AD = 4$代入$S=\frac{1}{2}BC\cdot AD$中，可得$24=\frac{1}{2}× x×4$，解得$x = 12$，即$BC = 12$。
2. 然后分情况讨论：
情况一：当点$D$在线段$BC$上时：
因为$BC=BD + CD$，已知$CD = 5$，$BC = 12$，根据$BD=BC - CD$，可得$BD=12 - 5=7$。
情况二：当点$D$在$BC$的延长线上时：
因为$BC=BD - CD$，已知$CD = 5$，$BC = 12$，根据$BD=BC + CD$，可得$BD=12 + 5=17$。
所以$BD$的长为$7$或$17$，答案是D。