第59页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1 [2024河北邯郸期末,中]如图,在正方形网格中有M,N两点,在直线l上找一点P使PM+PN的值最小,则点P应选在 (
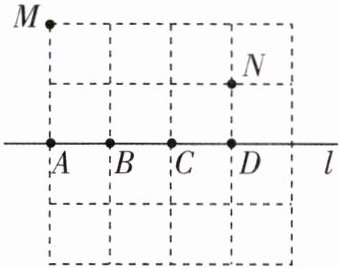
A.A点
B.B点
C.C点
D.D点
C
)
A.A点
B.B点
C.C点
D.D点
答案:
C 【解析】如图,点M'是点M关于直线l的对称点,连接M'N,则M'N与直线l的交点,即为点P,此时PM+PN的值最小.因为M'N与直线l交于点C,所以点P应选在C点.故选C.
如图,四边形ABCD中,$∠BAD= 120^{\circ },∠B= ∠D= 90^{\circ }$,在BC,CD上分别找一点M,N,使$\triangle AMN$的周长最小,则此时$∠AMN+∠ANM$的度数为 (
A.$130^{\circ }$
B.$120^{\circ }$
C.$110^{\circ }$
D.$100^{\circ }$
B
)A.$130^{\circ }$
B.$120^{\circ }$
C.$110^{\circ }$
D.$100^{\circ }$
答案:
B 【解析】如图,分别作A关于直线BC和CD的对称点A',A'',连接A'A'',交BC于M,交CD于N,则易得A'A''的长即为△AMN周长的最小值.因为∠DAB=120°,所以∠A'+∠A''=180°-∠DAB=60°.因为∠A'=∠MAA',∠NAD=∠A'',且∠A'+∠MAA'=180°-∠AMA'=∠AMN,∠NAD+∠A''=180°-∠ANA''=∠ANM,所以∠AMN+∠ANM=∠A'+∠MAA'+∠NAD+∠A''=2(∠A'+∠A'')=2×60°=120°.故选B.
3 AI DPSK原创[中]如图,在$\triangle ABC$中,$AD⊥BC,AC= AE,AD= 8,BC= 18$,点P为线段AD上一动点,点E是BC上一定点,点F是线段AB上一动点,则当$EP+FP$取最小值6时,AB的长为____
24
.
答案:
24 【解析】作E关于AD的对称点E',过E'作E'F⊥AB于F,交AD于P,如图.因为E关于AD的对称点为E',AD⊥BC,AC=AE,所以点E'与点C重合,所以PE+PF的最小值即为PE'+PF=CF,所以CF=6.由三角形的面积公式可知$\frac{1}{2}$×AB×CF=$\frac{1}{2}$×BC×AD=$\frac{1}{2}$×18×8,故AB=$\frac{8×18}{6}$=24.
如图,在锐角三角形ABC中,$AB= 6,\triangle ABC$的面积为18,BD平分$∠ABC$,若E,F分别是BD,BC上的动点,则$CE+EF$的最小值为 (
A.5
B.6
C.7
D.8
B
)A.5
B.6
C.7
D.8
答案:
B 【解析】如图,作点F关于直线BD的对称点G,连接CG,交BD于E,作CH⊥AB于H.由轴对称的性质易得CE+EF=CG.因为BD平分∠ABC,所以点G在AB上,所以CG≥CH,所以CE+EF的最小值为CH的长.因为$\frac{1}{2}$AB·CH=18,所以$\frac{1}{2}$×6CH=18,所以CH=6,所以CE+EF的最小值为6.故选B.
如图,在$\triangle ABC$中,$AB= AC,∠A= 90^{\circ }$,点D,E是边AB上的两个定点,点M,N分别是边AC,BC上的两个动点.当四边形DEMN的周长最小时,$∠DNM+∠EMN$的度数是 (
A.$45^{\circ }$
B.$90^{\circ }$
C.$75^{\circ }$
D.$135^{\circ }$
B
)A.$45^{\circ }$
B.$90^{\circ }$
C.$75^{\circ }$
D.$135^{\circ }$
答案:
B 【解析】如图,作点D关于直线BC的对称点D',作点E关于直线AC的对称点E',连接D'E'分别交AC,BC于点M',N',连接ME',ND',EM',DN'.由轴对称的性质可得ME=ME',ND=ND',所以四边形DEMN的周长为DE+ME+MN+ND=DE+ME'+MN+ND'≥DE+D'E'.因为DE的长固定,所以当点M与点M'重合,点N与点N'重合时,四边形DEMN的周长最小,此时∠DNM+∠EMN=∠DN'M'+∠EM'N'.由对称性、三角形内角和及平角的性质可知∠DN'M'=180°-∠DN'D'=∠N'DD'+∠N'D'D=2∠N'D'D,∠EM'N'=180°-∠EM'E'=∠M'EE'+∠M'E'E=2∠M'E'E,所以∠DN'M'+∠EM'N'=2∠N'D'D+2∠M'E'E=2(180°-∠D'DE').设DD'与BC交于点H.因为AB=AC,∠BAC=90°,所以易得∠BDH=45°,所以∠D'DE'=180°-45°=135°,所以∠DN'M'+∠EM'N'=2(180°-135°)=90°,即当四边形DEMN的周长最小时,∠DNM+∠ANM的度数是90°,故选B.
6 [2024山东泰安校级质检,中]如图,A,B两点都在直线MN的上方,$AB= 5$,A到直线MN的距离$AC= 8$,B到直线MN的距离$BD= 5$,P在直线MN上运动,则$|PA-PB|$的最大值等于
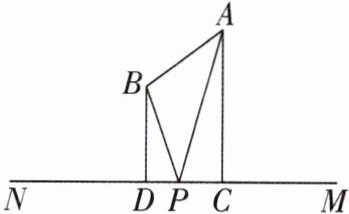
5
.
答案:
5 【解析】如图,延长AB交MN于点P'.因为P'A-P'B=AB,AB≥|PA-PB|,所以当点P运动到点P'的位置时,|PA-PB|的值最大.因为AB=5,所以|PA-PB|的最大值为5.故答案为5.
查看更多完整答案,请扫码查看


