第51页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
如图,在△ABC中,BD平分∠ABC,AD⊥BD,∠CAD= ∠C,若AB= 5,AD= 2,则BC的长为(
A.6
B.7
C.8
D.9
D
)A.6
B.7
C.8
D.9
答案:
D
如图,在平面直角坐标系xOy中,A(4,0),B(0,3),AB= 5.点D在x轴上,若在线段AB(包括两个端点)上找点P,使得以点A,D,P为顶点的等腰三角形的点P恰好只有1个,下列选项中不能满足上述条件的点D的坐标是(
A.(-3,0)
B.(-1,0)
C.(5,0)
D.(9,0)
B
)A.(-3,0)
B.(-1,0)
C.(5,0)
D.(9,0)
答案:
B
3[2024陕西西安校级期末,中]如图,AC= DC= 3,BD垂直于∠BAC的平分线AD,E为AC的中点,则 图中两个阴影三角形(△OBD与△OAE)的面积之差的最大值为
图中两个阴影三角形(△OBD与△OAE)的面积之差的最大值为
 图中两个阴影三角形(△OBD与△OAE)的面积之差的最大值为
图中两个阴影三角形(△OBD与△OAE)的面积之差的最大值为$\frac{9}{2}$
.
答案:
$\frac{9}{2}$
4[2025浙江宁波校级期末,中]如图(1),P为∠AOB的平分线OC上一点,过点P作PD//OB交OA于点D,易得△POD为等腰三角形.
(1)【基本运用】如图(2),把长方形纸片ABCD沿对角线AC折叠,使点B落在点B'处,AB'交CD于点E,△ACE是等腰三角形吗?为什么?
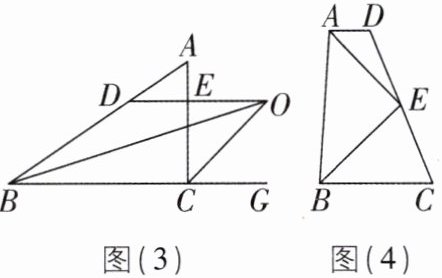
(2)【类比探究】如图(3),△ABC中,内角∠ABC与外角∠ACG的平分线交于点O,过点O作DO//BC分别交AB,AC于点D,E,试探究线段BD,DE,CE之间的数量关系并说明理由.
(3)【拓展提升】如图(4),四边形ABCD中,AD//BC,E为CD边的中点,AE平分∠BAD,连接BE,求证:AE⊥BE.

(1)【基本运用】如图(2),把长方形纸片ABCD沿对角线AC折叠,使点B落在点B'处,AB'交CD于点E,△ACE是等腰三角形吗?为什么?
(2)【类比探究】如图(3),△ABC中,内角∠ABC与外角∠ACG的平分线交于点O,过点O作DO//BC分别交AB,AC于点D,E,试探究线段BD,DE,CE之间的数量关系并说明理由.
(3)【拓展提升】如图(4),四边形ABCD中,AD//BC,E为CD边的中点,AE平分∠BAD,连接BE,求证:AE⊥BE.


答案:
(1)△ACE是等腰三角形.理由:在长方形ABCD中,
∵DC//AB,
∴∠ACD=∠BAC;由折叠的性质可得∠BAC=∠B'AC,
∴∠ACD=∠B'AC,
∴AE=CE,
∴△ACE是等腰三角形.
(2)BD=DE+CE.理由:同
(1)可证△BDO为等腰三角形,则BD=OD.
∵CO平分∠ACG,DO//BC,
∴∠OCG=∠ECO=∠EOC,
∴CE=OE,
∴BD=DO=DE+EO=DE+CE.
(3)如图,延长AE交BC的延长线于F.
∵AD//BC,
∴∠F=∠DAE,∠D=∠ECF.
∵AE平分∠BAD,
∴∠BAF=∠DAF,
∴∠BAF=∠F,
∴BA=BF.
∵E是CD的中点,
∴DE=CE.在△ADE和△FCE中,∠DAE=∠CFE,∠ADE=∠FCE,DE=CE,
∴△ADE≌△FCE(AAS),
∴AE=EF,
∴点E是AF的中点,
∴BE⊥AE.

(1)△ACE是等腰三角形.理由:在长方形ABCD中,
∵DC//AB,
∴∠ACD=∠BAC;由折叠的性质可得∠BAC=∠B'AC,
∴∠ACD=∠B'AC,
∴AE=CE,
∴△ACE是等腰三角形.
(2)BD=DE+CE.理由:同
(1)可证△BDO为等腰三角形,则BD=OD.
∵CO平分∠ACG,DO//BC,
∴∠OCG=∠ECO=∠EOC,
∴CE=OE,
∴BD=DO=DE+EO=DE+CE.
(3)如图,延长AE交BC的延长线于F.
∵AD//BC,
∴∠F=∠DAE,∠D=∠ECF.
∵AE平分∠BAD,
∴∠BAF=∠DAF,
∴∠BAF=∠F,
∴BA=BF.
∵E是CD的中点,
∴DE=CE.在△ADE和△FCE中,∠DAE=∠CFE,∠ADE=∠FCE,DE=CE,
∴△ADE≌△FCE(AAS),
∴AE=EF,
∴点E是AF的中点,
∴BE⊥AE.

5思想方法分类讨论[2024广东湛江期末,较难]
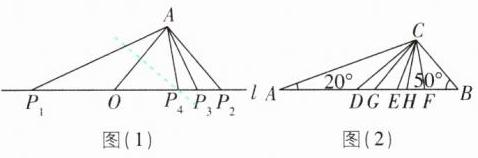
(1)如图(1),线段OA的一个端点O在直线l上,且与直线l所成的锐角为50°,以OA为一边画等腰三角形,并且使另一个顶点P在直线l上,这样的等腰三角形能画______个.
(2)如图(2),△ABC中,∠A= 20°,∠B= 50°,过顶点C作一条直线,把该三角形分割出一个小等腰三角形,这样的直线最多可以画______条.
(3)如图(3),在△ABC中,∠BAC= 10°,若存在过点C的一条直线,能把该三角形分成两个小等腰三角形,试求∠B的度数.

(1)如图(1),线段OA的一个端点O在直线l上,且与直线l所成的锐角为50°,以OA为一边画等腰三角形,并且使另一个顶点P在直线l上,这样的等腰三角形能画______个.
(2)如图(2),△ABC中,∠A= 20°,∠B= 50°,过顶点C作一条直线,把该三角形分割出一个小等腰三角形,这样的直线最多可以画______条.
(3)如图(3),在△ABC中,∠BAC= 10°,若存在过点C的一条直线,能把该三角形分成两个小等腰三角形,试求∠B的度数.

答案:
(1)4
(2)5
(3)如图
(3),当AD=CD时,∠ACD=∠A=10°,
∴∠CDB=20°,
∴①当CD=BD时,∠B=∠BCD=80°;②当CD=BC时,∠B=∠CDB=20°;③当BD=BC时,∠B=180°−20°−20°=140°.如图
(4),当AC=AE,CE=BE时,
∵∠A=10°,
∴∠ACE=∠AEC=85°,
∴∠B=∠BCE=42.5°.如图
(5),当AC=CF,CF=BF时,
∵∠A=10°,
∴∠AFC=∠A=10°,
∴∠B=5°.综上所述,∠B的度数为80°或20°或140°或42.5°或5°.
(1)4
(2)5
(3)如图
(3),当AD=CD时,∠ACD=∠A=10°,
∴∠CDB=20°,
∴①当CD=BD时,∠B=∠BCD=80°;②当CD=BC时,∠B=∠CDB=20°;③当BD=BC时,∠B=180°−20°−20°=140°.如图
(4),当AC=AE,CE=BE时,
∵∠A=10°,
∴∠ACE=∠AEC=85°,
∴∠B=∠BCE=42.5°.如图
(5),当AC=CF,CF=BF时,
∵∠A=10°,
∴∠AFC=∠A=10°,
∴∠B=5°.综上所述,∠B的度数为80°或20°或140°或42.5°或5°.

查看更多完整答案,请扫码查看


