《2025年初中必刷题八年级数学上册人教版》

1 [2025 浙江绍兴质检]如图(1),正方形被划分成 16 个全等的三角形,将其中若干个三角形涂黑,且满足下列条件:
(1)涂黑部分的面积是原正方形面积的一半;
(2)涂黑部分中存在全等图形.
如图(2)是一种涂法,请在图(4)、(5)、(6)中分别设计另外三种不同的涂法.(在所设计的图案中,若涂黑部分全等,则认为是同一种涂法,如图(2)与图(3))

答案：
1.【解】如图
(1)、
(2)、
(3).（答案不唯一）

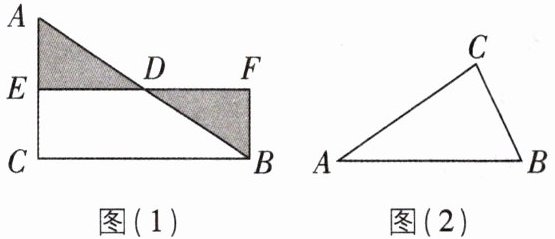
2 [2025 贵州遵义期末]如图(1),Rt△ABC 中,∠C = 90°,D 是 AB 的中点,过点 D 作 DE⊥AC 于点 E,过点 B 作 BF⊥ED,交 ED 的延长线于点 F.
(1)求证:△DFB≌△DEA.
(2)某数学兴趣小组解答(1)后发现,在图中只需将△AED 剪下来拼到△BFD 处,就可得到一个与图(1)中△ABC 等面积的长方形 EFBC. 继续讨论后又发现,任意三角形也可以剪拼成一个等面积的长方形,请你在图(2)中画出一种剪拼示意图,并简要说明作法(不需要证明).

答案：
2.
(1)【证明】
∵DE⊥AC,BF⊥ED,D 是 AB 的中点，
∴∠AED=∠BFD=90°,AD=BD.
∵∠ADE=∠BDF,
∴△DFB≌△DEA.
(2)【解】(画出一种即可,答案不唯一,给出以下三种作法供参考)如图.

作法①:找 AC,BC 的中点,过两中点作一条直线,分别过点 A,B 作该直线的垂线,得到的以AB 为边的长方形与△ABC 的面积相等.
作法②:找 AC,AB 的中点,过两中点作一条直线,分别过点 B,C 作该直线的垂线,得到的以BC 为边的长方形与△ABC 的面积相等.
作法③:找 AB,BC 的中点,过两中点作一条直线,分别过点 A,C 作该直线的垂线,得到的以AC 为边的长方形与△ABC 的面积相等.
多解
(2)如图,分别过 AC,BC 的中点 M,N 作 AB 的垂线,垂足分别为 O,P,再过点 C 作 AB 的平行线,与 OM,PN 的延长线交于点 E,F,则长方形 OPFE 的面积与△ABC 的面积相等.

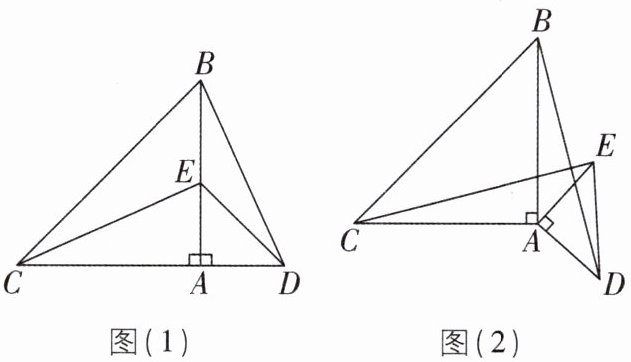
3 [2025 广东肇庆质检]小明和小华各买了一副大小不同的三角板. 小明把他们两人的等腰直角三角板的直角的顶点和一直角边叠在一起拼成如图(1)的图形(△ABC 和△ADE),∠BAC = ∠DAE = 90°,AB = AC,AD = AE,连接 BD,CE.
(1)求证:BD = CE.
(2)小华把小明的拼图动了一下,但两块三角板的直角顶点还是叠在一起的,如图(2),请问 BD 和 CE 还相等吗? 证明你的结论.
(3)请分别指出两个拼图中,BD 与 CE 的位置关系,不用说明理由.

答案：
3.
(1)【证明】在△ABD 与△ACE 中,
{AB=AC,
∠BAD=∠CAE=90°,
AD=AE,
∴△ABD≌△ACE(SAS),
∴BD=CE.
(2)【解】BD=CE.证明:
∵∠BAC=∠DAE=90°,
∴∠BAC+∠BAE=∠DAE+∠BAE,即∠CAE=∠BAD.在△ABD 与△ACE 中,
{AB=AC,
∠BAD=∠CAE,
AD=AE,
∴△ABD≌△ACE(SAS),
∴BD=CE.
(3)【解】两个拼图中,BD 与 CE 的位置关系均为互相垂直.如图
(1),延长 CE 交 BD 于 F.
∵△ABD≌△ACE,
∴∠ADB=∠AEC.
∵∠ABD+∠ADB=90°,∠AEC=∠BEF,
∴∠ABD+∠BEF=90°,
∴CE⊥BD.如图
(2),设 AB 与CE 交于 F.
∵△ABD≌△ACE,
∴∠ACE=∠ABD.
∵∠ACF+∠AFC=90°,∠AFC=∠BFE,
∴∠ABD+∠BFE=90°,
∴CE⊥BD.
　　　 　　
思路分析
(2)先证明∠BAD=∠CAE,再根据 SAS 证明△ABD≌△ACE,可得答案.