《2025年初中必刷题八年级数学上册人教版》

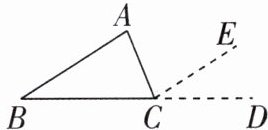
1[2024山东烟台期中]如图,在证明△ABC内角和等于180°时,延长BC至D,过点C作CE//AB,得到∠ABC= ∠ECD,∠BAC= ∠ACE,由于∠BCD= 180°,可得到∠ABC+∠ACB+∠BAC= 180°,这个证明方法体现的数学思想是(D)

A.数形结合
B.特殊到一般
C.一般到特殊
D.转化

答案： D　[解析]
∵CE//AB,
∴∠ABC=∠ECD,∠BAC=∠ACE.
∵∠BCD=180°,即∠ECD+∠ACB+∠ACE=180°,
∴∠ABC+∠ACB+∠BAC=180°,这个证明方法体现了转化的数学思想，故选D.

在△ABC中,∠A:∠B:∠C= 1:2:6,则此三角形是(C)
A.锐角三角形
B.直角三角形
C.钝角三角形
D.无法判断

答案： C　[解析]
∵∠A:∠B:∠C=1:2:6,
∴设∠A=x,∠B=2x,∠C=6x.
∵∠A+∠B+∠C=180°,即x+2x+6x=180°,解得x=20°,
∴最大角为∠C=120°,
∴此三角形是钝角三角形，故选C.

如图,在△ABC中,∠A= 40°,∠B= 68°,E是△ABC的角平分线CF延长线上一动点(不与F点重合),过E点作ED⊥AB于D点,当E点运动时,∠E的度数(D)
A.随E点运动而变化,离F点越近,度数越大
B.不变,为16°
C.随E点运动而变化,离F点越远,度数越大
D.不变,为14°

答案： D　[解析]
∵∠A=40°,∠B=68°,∠A+∠B+∠BCA=180°,
∴∠BCA=180°−40°−68°=72°.
∵CF平分∠BCA,
∴∠BCF=$\frac{1}{2}$∠BCA=36°,
∴∠BFC=∠EFD=180°−36°−68°=76°.
∵ED⊥AB,
∴∠FDE=90°,
∴∠FED=180°−90°−76°=14°,
∴当E点运动时,∠E的度数不变,为14°.故选D.

4[2024上海黄浦区调研]如图,在△ABC中,∠C= 60°,按图中虚线将∠C剪去后,∠1+∠2= ____.

答案：
240°　[解析]如图.
∵∠1+∠DEC=180°,∠2+∠EDC=180°,
∴∠1+∠2+∠DEC+∠EDC=360°.
∵∠C=60°，
∴∠DEC+∠EDC=180°−60°=120°,
∴∠1+∠2=360°−(∠DEC+∠EDC)=240°,故答案为240°.

5[2025江西南昌质检]【模型理解】(1)如图(1),AB和CD交于点O,求证:∠A+∠C= ∠B+∠D;
【模型应用】(2)如图(2),AE,CE分别平分∠BAD,∠BCD,求证:∠B+∠D= 2∠E.

答案： [证明]
(1)在△AOC中,∠A+∠C+∠AOC=180°,在△BOD中,∠B+∠D+∠BOD=180°.
∵∠AOC=∠BOD,
∴∠A+∠C=∠B+∠D.
(2)同
(1)中模型可得,在△ABF和△CEF中,有∠B+∠BAF=∠E+∠ECF,在△CDG和△AEG中,有∠D+∠DCE=∠E+∠EAD,
∴∠B+∠D+∠DCE+∠BAF=2∠E+∠ECF+∠EAD.
∵AE,CE分别平分∠BAD,∠BCD,
∴∠DCE=∠ECF,∠BAF=∠EAD,
∴∠B+∠D=2∠E.

6[2025河南周口期中]如图所示,以下描述错误的是( )


A.点A位于点B北偏西20°方向
B.点A位于点C北偏东40°方向
C.点C位于点B北偏西63°方向
D.∠ABC= 53°

答案：
C　[解析]如图.由题意得AD//BE,
∴∠ABE=∠BAD=20°,
∴∠CAB=40°+20°=60°.
∵∠ACB=67°,
∴∠ABC=180°−∠ACB−∠BAC=53°,
∴∠CBE=∠ABC+∠ABE=73°.A选项，点A位于点B北偏西20°方向，故A不符合题意;B选项，点A位于点C北偏东40°方向，故B不符合题意;C选项，点C位于点B北偏西73°方向，故C符合题意;D选项，∠ABC=53°,故D不符合题意.故选C.

7[2025广东深圳期中]如图,∠P的两边被一张长方形纸片遮挡部分,若∠1= 120°,∠2= 68°,则∠P= ____.

答案：
52°　[解析]如图,由题意可得∠1=∠3=120°，
∴∠4=180°−120°=60°.
∵∠2=68°,
∴∠P=180°−∠2−∠4=180°−68°−60°=52°.故答案为52°.