《2025年初中必刷题八年级数学上册人教版》

1 [中]如图,在△ABC中,AB= AC,AB＞BC,点D在边BC上,CD= 2BD,点E,F在线段AD上,∠1= ∠2= ∠BAC,若△ABC的面积为18,则△ACF与△BDE的面积之和是(A)

A.6
B.8
C.9
D.12

答案： 1. 首先，利用三角形面积公式$S = \frac{1}{2}ah$（$a$为底，$h$为高）：
已知$CD = 2BD$，设$BD=x$，则$CD = 2x$，$BC=BD + CD=3x$。
因为$\triangle ABC$与$\triangle ABD$、$\triangle ACD$等高（设高为$h$，$h$是$A$到$BC$的距离），根据$S=\frac{1}{2}ah$，$S_{\triangle ABC}=\frac{1}{2}BC\cdot h$，$S_{\triangle ABD}=\frac{1}{2}BD\cdot h$，$S_{\triangle ACD}=\frac{1}{2}CD\cdot h$。
所以$S_{\triangle ABD}=\frac{BD}{BC}S_{\triangle ABC}$，$S_{\triangle ACD}=\frac{CD}{BC}S_{\triangle ABC}$。
把$BC = 3x$，$BD=x$，$CD = 2x$，$S_{\triangle ABC}=18$代入可得：$S_{\triangle ABD}=\frac{1}{3}×18 = 6$，$S_{\triangle ACD}=\frac{2}{3}×18 = 12$。
2. 然后，证明$\triangle ABE\cong\triangle CAF$：
因为$\angle1=\angle2=\angle BAC$，$\angle BAC=\angle BAE+\angle CAF$，$\angle2=\angle FCA+\angle CAF$，所以$\angle BAE=\angle FCA$。
又因为$\angle1=\angle2$，$AB = AC$。
在$\triangle ABE$和$\triangle CAF$中，$\left\{\begin{array}{l}\angle BAE=\angle FCA\\\angle1=\angle2\\AB = AC\end{array}\right.$。
根据$AAS$（两角及其中一角的对边对应相等的两个三角形全等），可得$\triangle ABE\cong\triangle CAF$。
所以$S_{\triangle ABE}=S_{\triangle CAF}$。
3. 最后，求$S_{\triangle ACF}+S_{\triangle BDE}$的值：
因为$S_{\triangle ACF}+S_{\triangle BDE}=S_{\triangle ABE}+S_{\triangle BDE}$。
而$S_{\triangle ABE}+S_{\triangle BDE}=S_{\triangle ABD}$。
所以$\triangle ACF$与$\triangle BDE$的面积之和是$6$，答案是A。

2 [2025河北唐山期中,中]已知在△AOB中,∠AOB= 90°,OA= OB,直线l经过∠AOB的顶点O(l不与∠AOB的两边重合),作AC⊥l,BD⊥l,垂足分别为C,D.甲、乙两位同学给出自己的结论:
甲:当直线l穿过△AOB内部时,DC= BD-AC;
乙:当直线l在△AOB外部时,DC= BD+AC.
对于上述两个结论,下列说法正确的是( )

A.只有甲正确
B.只有乙正确
C.甲、乙都正确
D.甲、乙都不正确

答案：
B 【解析】如图
(1)，
∵AC⊥l，BD⊥l，
∴∠ACO = ∠ODB = 90°，
∴∠OAC + ∠AOC = 90°。
∵∠AOB = 90°，
∴∠AOC + ∠BOD = 90°，
∴∠OAC = ∠BOD。在△ACO 和△ODB 中，∠ACO = ∠ODB，∠OAC = ∠BOD，OA = BO，
∴△ACO≌△ODB(AAS)，
∴AC = OD，OC = BD，
∴DC = OD - OC = AC - BD，故甲不正确。

如图
(2)，
∵AC⊥l，BD⊥l，
∴∠ACO = ∠ODB = 90°，
∴∠OAC + ∠AOC = 90°。
∵∠AOB = 90°，
∴∠AOC + ∠BOD = 90°，
∴∠OAC = ∠BOD。在△ACO 和△ODB 中，∠ACO = ∠ODB，∠OAC = ∠BOD，OA = OB，
∴△ACO≌△ODB(AAS)，
∴AC = OD，OC = BD，
∴DC = OD + OC = AC + BD，故乙正确。故选B。

3 [2024湖北宜昌校级质检,中]如图,在△ABC中,∠ACB= 90°,AC= BC,点A的坐标为(-6,3),点C的坐标为(-1,0),则点B的坐标是______.

答案：
(2,5) 【解析】作AD⊥x 轴于点D，BE⊥x 轴于点E，如图所示，则∠ADC = ∠CEB = 90°，
∴∠ACD + ∠CAD = 90°。
∵∠ACB = 90°，
∴∠ACD + ∠BCE = 90°，
∴∠CAD = ∠BCE。在△ACD 和△CBE 中，∠ADC = ∠CEB，∠CAD = ∠BCE，AC = CB，
∴△ACD≌△CBE(AAS)，
∴AD = CE，DC = EB。
∵点A 的坐标为(-6,3)，点C 的坐标为(-1,0)，
∴OD = 6，AD = 3，OC = 1，
∴CE = 3，BE = OD - OC = 6 - 1 = 5，
∴OE = CE - OC = 3 - 1 = 2，
∴点B 的坐标为(2,5)。故答案为(2,5)。

4 [难]如图,AE与BD相交于点C,AC= EC,BC= DC,AB= 4 cm,点P从点A出发,沿A→B→A方向以3 cm/s的速度运动,点Q从点D出发,沿D→E方向以1 cm/s的速度运动,P,Q两点同时出发,当点P返回到点A时,P,Q两点同时停止运动.设点P的运动时间为t s.连接PQ,当线段PQ经过点C时,t的值为______.

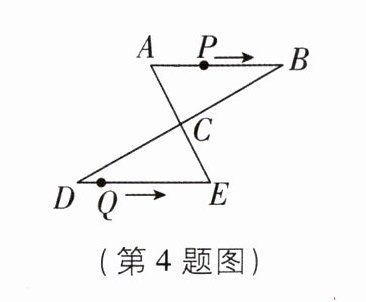
答案：
1 或 2 【解析】如图，在△ABC 和△EDC 中，AC = EC，∠ACB = ∠ECD，BC = DC，
∴△ABC≌△EDC(SAS)，
∴∠A = ∠E，ED = AB = 4 cm。在△ACP 和△ECQ 中，∠A = ∠E，AC = CE，∠ACP = ∠ECQ，
∴△ACP≌△ECQ(ASA)，
∴AP = EQ。当0≤t≤$\frac{4}{3}$时，3t = 4 - t，解得t = 1；当$\frac{4}{3}$ ＜ t≤$\frac{8}{3}$时，8 - 3t = 4 - t，解得t = 2。综上所述，当线段PQ 经过点C 时，t 的值为1 或 2。故答案为1 或 2。

5 核心素养推理能力[2024陕西渭南期末,较难]问题提出:
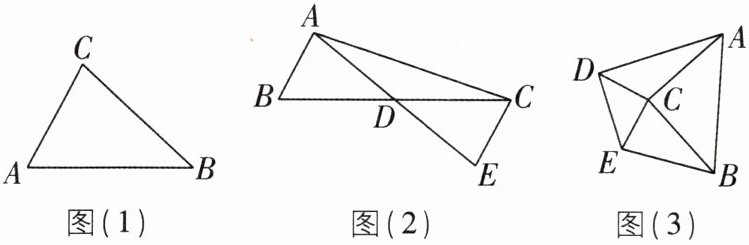
(1)我们把两个面积相等但不全等的三角形叫作偏等积三角形.如图(1),△ABC中,AC= 8,BC= 9,AB= 10,P为AC上一点,当AP= ______时,△ABP与△CBP是偏等积三角形.
问题探究:
(2)如图(2),△ABD与△ACD是偏等积三角形,AB= 2,AC= 6,且线段AD的长度为正整数,过点C作CE//AB交AD的延长线于点E,则AD的长为______.
问题解决:
(3)如图(3),C为四边形ABED内的一点,CA= CB,CD= CE,∠ACB= ∠DCE= 90°(0°＜∠BCE＜90°).△ACD与△BCE是偏等积三角形吗?请说明理由.

答案：
【解】
(1)如图
(1)，取AC 中点P，连接BP。
∵△ABP 与△CBP 在AP，CP 边上的高相等，
∴当AP = CP = $\frac{1}{2}$AC = $\frac{1}{2}× 8 = 4$时，△ABP 与△CBP 面积相等。
∵BC = 9，AB = 10，
∴BC≠AB。
∵AP = CP，BP = BP，BC≠AB，
∴△ABP 与△CBP 不全等，
∴当AP = 4 时，△ABP 与△CBP 是偏等积三角形，故答案为4。

(2)
∵△ABD 与△ACD 是偏等积三角形，且△ABD 与△ACD 在BD，CD 边上的高相等，
∴BD = CD。
∵CE//AB，
∴∠E = ∠BAD。在△ECD 和△ABD 中，∠E = ∠BAD，∠EDC = ∠ADB，CD = BD，
∴△ECD≌△ABD(AAS)，
∴ED = AD，EC = AB = 2。
∵AC - EC ＜ AE ＜ AC + EC，且AC = 6，AE = 2AD，
∴6 - 2 ＜ 2AD ＜ 6 + 2，
∴2 ＜ AD ＜ 4。
∵线段AD 的长度为正整数，
∴AD = 3，故答案为3。
(3)△ACD 与△BCE 是偏等积三角形。理由：
∵∠ACB = ∠DCE = 90°，
∴∠ACD + ∠BCE = 180°。
∵0° ＜ ∠BCE ＜ 90°，
∴∠ACD ＞ 90°，
∴∠ACD≠∠BCE。
∵CA = CB，CD = CE，
∴△ACD 与△BCE 不全等。如图
(2)，作BF⊥CE 于点F，AG⊥DC 交DC 的延长线于点G，则∠G = ∠BFC = 90°。
∵∠ECG = 180° - ∠DCE = 90°，
∴∠ACG = ∠BCF = 90° - ∠BCG。在△ACG 和△BCF 中，∠G = ∠BFC，∠ACG = ∠BCF，CA = CB，
∴△ACG≌△BCF(AAS)，
∴AG = BF，
∴$\frac{1}{2}CD\cdot AG=\frac{1}{2}CE\cdot BF$，
∴△ACD 与△BCE 面积相等，
∴△ACD 与△BCE 是偏等积三角形。