《2025年初中必刷题八年级数学上册人教版》

1 [2024 北京海淀区期中,中]如图,在直角三角形ABC中,∠ABC= 90°,点D沿CB自点C向点B运动(点D与点C,B不重合),作BE⊥AD于点E,CF⊥AD的延长线于点F,在点D的运动过程中,BE+CF的值逐渐(B)

A.变小
B.变大
C.不变
D.无法确定

答案： B

如图,点E是长方形ABCD内任意一点,连接AE,BE,CE,DE把长方形分成4个三角形,将△ABE,△BCE,△CDE,△ADE的面积分别记为$S_1,S_2,S_3,S_4.$已知长方形的面积,则一定可求出的值是(D)
$A. S_1 B. S_1+S_2 C. S_1+S_2+S_3 D. S_1+S_3$

答案： D

3 [中]如图,在△ABC中,AD为BC边上的中线,DE⊥AB于点E,DF⊥AC于点F,AB= 3,AC= 4,DF= 1.5,则DE= ______.

2

答案： 2

4 [2024 湖北武汉调研,中]如图,点G为△ABC的重心,CF⊥BE于G,若AG×BC= 16,则△BGC面积的最大值是______4.

答案： 4

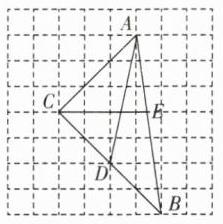
5 [2025 安徽合肥期中,中]如图,在每个小正方形边长都为1的方格纸中,△ABC的顶点都在方格纸的格点(小正方形的顶点)上.
(1)通过观察,可以发现△ABC是( )

A. 锐角三角形 B. 钝角三角形 C. 直角三角形 D. 直角三角形或锐角三角形
(2)仅利用无刻度的直尺画出△ABC的中线AD与角平分线CE.
(3)△ABC的面积为______,△ABD的面积为______.

答案：

(1)C；
(2)如图，线段 AD 即为所求作的△ABC 的中线，线段 CE 即为所求作的△ABC 的角平分线.；
(3)12，6

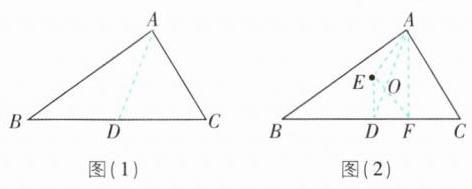
6 核心素养 模型观念 [较难]如图(1),有一块三角形菜地,若从顶点A修一条笔直的小路交BC于点D,小路正好将菜地分成面积相等的两部分.
(1)找出D点的位置并说明理由.
(2)假设在菜地中有一点E,如图(2)所示,BC上是否存在点F,使折线A-E-F将△ABC分为面积相等的两部分?若存在,请找出F点的位置,并说明理由.

答案：
【解】
(1)如图
(1)，取 BC 的中点 D，点 D 即为所求. 理由：连接 AD.
∵ D 为 BC 中点，
∴ BD=CD，
∴ △ABD 与△ACD 等底同高，
∴ $S_{△ABD}=S_{△ACD}$.；
(2)存在. 如图
(2)，取 BC 的中点 D，连接 AD，AE，DE，过点 A 作 AF//DE，交 BC 于点 F，点 F 即为所求. 理由如下：连接 EF 交 AD 于 O.
∵ BD=CD，
$∴S_{△ADB}=S_{△ADC}.$
∵ DE//AF，
∴ 点 D 到 AF 的距离与点 E 到 AF 的距离相等，
$∴ S_{△AEF}=S_{△ADF}$
$∴ S_{△AEO}=S_{△DFO}$
$∴S_{四边形ABFE}=S_{四边形AEFC}$