《2025年初中必刷题八年级数学上册人教版》

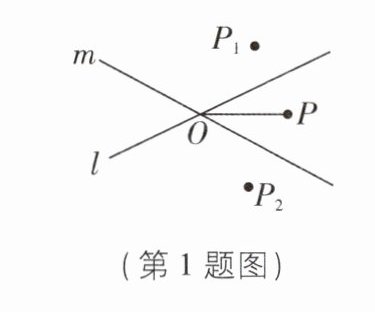
1 [中] 如图,直线 l,m 相交于点 O,P 为这两直线外一点,且 OP = 2.8. 若点 P 关于直线 l,m 对称的点分别是点$ P_1,P_2,$则$ P_1,P_2 $之间的距离可能是 ( )

A.0
B.5
C.6
D.7

答案：
B　[解析]如图，连接OP₁，OP₂，P₁P₂，PP₁，PP₂.
∵点P关于直线l，m的对称点分别是点P₁，P₂，
∴直线l垂直平分PP₁，直线m垂直平分PP₂，
∴OP₁=OP=OP₂=2.8.根据三角形三边关系定理可知OP₁-OP₂＜P₁P₂＜OP₁+OP₂，即0＜P₁P₂＜5.6，故选B.

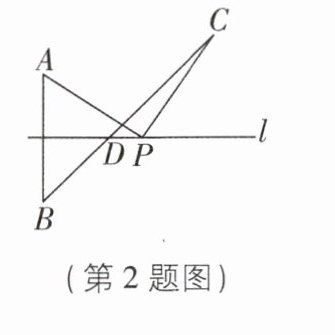
2 [2025 河北承德质检,中] 如图,直线 l 是线段 AB 的垂直平分线,点 C 在直线 l 外,且与点 A 在直线 l 的同侧,连接 BC,交直线 l 于点 D,点 P 是直线 l 上的一个动点(不与点 D 重合),连接 AP,CP,则 BC 与 AP + PC 的大小关系是 ( )

A.BC ＞ AP + PC
B.BC ＜ AP + PC
C.BC = AP + PC
D.不能确定

答案：
B　[解析]如图，连接BP.
∵直线l是线段AB的垂直平分线，
∴AP=BP，
∴AP+PC=BP+PC.
∵点P不与点D重合，
∴AP+PC=BP+PC＞BC.故选B.

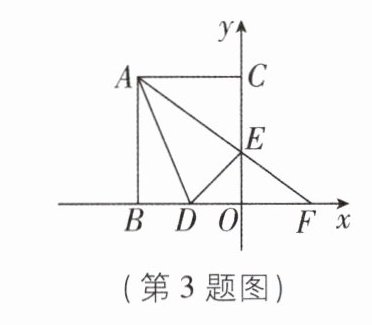
3 [2025 湖南湘西州期中,中] 如图,长方形 ABOC 的顶点 A 的坐标为(-4,5),D 是 OB 的中点,E 是 OC 上的一点,AE 的延长线交 x 轴于 F,当△ADE 的周长最小时,△ADF 的面积是 ( )

A.6
B.8
C.10
D.12

答案：
C　[解析]
∵长方形ABOC的顶点A的坐标为(−4，5)，D是OB的中点，
∴AB⊥BO，OC⊥AC，
∴AB=5，OB=4，
∴OD= $\frac{1}{2}$OB=2.如图，作点A关于y轴的对称点A'，连接A'E.由轴对称的性质可得A'C=AC.
∵OC⊥AC，
∴CO垂直平分AA'，
∴AE=A'E，
∴△ADE的周长=AD+AE+DE=AD+A'E+DE，
∴当A'，E，D三点在同一条直线上时，A'E+DE的值最小，即△ADE的周长最小，易得此时OF=OD=2，
∴DF=OD+OF=4，
∴△ADF的面积是 $\frac{1}{2}$DF·AB= $\frac{1}{2}$×4×5=10，故选C.

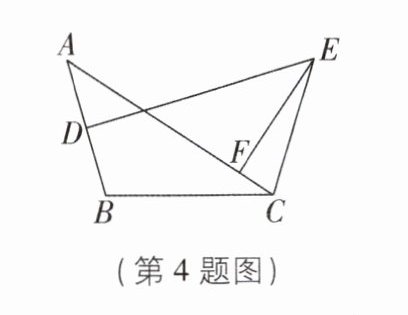
4 [中] 如图,在△ABC 中,D 是 AB 的中点,DE ⊥ AB,∠ACE + ∠BCE = 180°,EF ⊥ AC 交 AC 于 F,AC = 6,BC = 4,则 AF = ____.

答案：
5　[解析]如图，连接AE，BE，过点E作EG⊥BC交BC的延长线于点G.
∵D是AB的中点，DE⊥AB，
∴DE垂直平分线段AB，
∴AE=BE.
∵∠ACE+∠BCE=180°，∠ECG+∠BCE=180°，
∴∠ACE=∠ECG，
∴CE是∠ACG的平分线.
∵EF⊥AC，EG⊥BC，
∴EF=EG.又
∵CE=CE，
∴Rt△EFC≌Rt△EGC(HL)，
∴CF=CG.在Rt△AEF和Rt△BEG中，$\begin{cases} EA=EB, \\ EF=EG, \end{cases}$
∴Rt△AEF≌Rt△BEG(HL)，
∴AF=BG.设CF=CG=x，则AF=AC-CF=6-x，BG=BC+CG=4+x，
∴6-x=4+x，解得x=1，
∴AF=6-1=5.

5 [2024 广东广州期末,中] 如图,在平面直角坐标系中,点 A(4,0),B(0,8),点 C 在 AB 的垂直平分线上,且∠ACB = 90°,则点 C 的坐标为____.

答案：
(6，6)或(−2，2)　[解析]分两种情况：
(1)如图
(1)所示，过点C作CD⊥OB于D，CE⊥x轴于E.
∵∠BCA=∠DCE=90°，
∴∠BCD=∠ACE=90°-∠ACD.
∵点C在AB的垂直平分线上，
∴BC=AC.在△BCD与△ACE中，$\begin{cases} ∠BDC=∠AEC=90°, \\ ∠BCD=∠ACE, \\ BC=AC, \end{cases}$
∴△BCD≌△ACE(AAS)，
∴AE=BD，CE=CD=OE.
∵OA=4，OB=8，
∴4+AE=8-AE，
∴AE=2，
∴OE=OD=6，则点C坐标为(6，6).

如图
(2)所示，过点C作CD⊥OB于D，CE⊥x轴于E.
∵∠BCA=∠DCE=90°，
∴∠BCD=∠ACE=90°-∠ACD.
∵点C在AB的垂直平分线上，
∴BC=AC.在△BCD与△ACE中，$\begin{cases} ∠BDC=∠AEC=90°, \\ ∠BCD=∠ACE, \\ BC=AC, \end{cases}$
∴△BCD≌△ACE(AAS)，
∴AE=BD，CE=CD=OE，
∴4+OE=8-OE，
∴OE=2，则点C坐标为(−2，2).综上可知点C坐标为(6，6)或(−2，2).故答案为(6，6)或(−2，2).

6 [2025 河北邯郸质检,中] 如图,点 P 在∠AOB 的平分线上,点 E,F 分别在 OA,OB 上,且∠OFP = ∠OEP.
(1)求证:PF = PE.
(2)延长 FP,EP,分别交 OA,OB 于点 C,D,连接 CD,若 DP 平分∠CDB,回答下列问题:
①试说明 CP 平分∠ACD;
②若$ CD = 2,S_{△PCD} = 2,$求点 P 到射线 OA 的距离.

答案：

(1)[证明]
∵点P在∠AOB的平分线上，
∴∠EOP=∠FOP.又
∵∠OFP=∠OEP，OP=OP，
∴△OFP≌△OEP(AAS)，
∴PF=PE.
(2)[解]①如图，过点P作OA，OB，CD的垂线，垂足分别为I，G，H.

∵点P在∠AOB的平分线上，
∴PG=PI.
∵DP平分∠CDB，
∴PG=PH，
∴PH=PI，
∴CP平分∠ACD.
②由
(1)得△OFP≌△OEP，
∴OF=OE.又
∵∠OFC=∠OED，∠FOC=∠EOD，
∴△FOC≌△EOD(ASA)，
∴OD=OC，DE=CF.
∵PF=PE，
∴PD=PC，
∴OP是线段CD的垂直平分线，则点H是OP与CD的交点.
∵CD=2，$S_{△PCD}=2$，
∴$\frac{1}{2}$×CD×PH=2，
∴PH=2，
∴PH=PI=2，即点P到射线OA的距离为2.

7 核心素养推理能力 [中] 如图,在四边形 ABCD 中,∠A = ∠B = 90°,AB = 25 cm,DA = 15 cm,CB = 10 cm. 动点 E 从 A 点出发,以 2 cm/s 的速度向 B 点移动,设移动的时间为 x s.
(1)当 x 为何值时,点 E 在线段 CD 的垂直平分线上? 并说明理由.
(2)在(1)的条件下,判断 DE 与 CE 的位置关系,并说明理由.

答案： [解]
(1)当x=5时，点E在线段CD的垂直平分线上.理由：当x=5时，AE=2×5=10(cm).
∵AB=25cm，DA=15cm，CB=10cm，
∴BE=AD=15cm，AE=BC=10cm.在△ADE和△BEC中，$\begin{cases} AD=BE, \\ ∠A=∠B, \\ AE=BC, \end{cases}$
∴△ADE≌△BEC(SAS)，
∴DE=CE，
∴点E在线段CD的垂直平分线上.故当x=5时，点E在线段CD的垂直平分线上.
(2)DE与CE的位置关系是DE⊥CE.理由：
∵△ADE≌△BEC，
∴∠ADE=∠CEB.
∵∠A=90°，
∴∠ADE+∠AED=90°，
∴∠AED+∠CEB=90°，
∴∠DEC=180°-(∠AED+∠CEB)=90°，
∴DE⊥CE.