《2025年初中必刷题八年级数学上册人教版》

1[2025吉林长春期末]如图,以点O为圆心,适当长为半径作弧,交OM于点A,交ON于点B,分别以点A,B为圆心,大于$\frac {1}{2}AB$的长为半径作弧,两弧在$∠MON$的内部相交于点C,作射线OC.
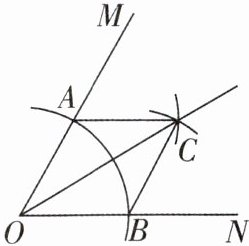
(1)根据以上尺规作图的过程可得到结论:射线OC为$∠MON$的平分线.
(2)连接AC,BC,运用三角形全等的相关判定方法证明(1)中的结论.

[证明]由作图过程可得,OA=OB,AC=BC.在△AOC和△BOC中,OA=OB,OC=OC,AC=BC,∴△AOC≌△BOC(SSS),∴∠AOC=∠BOC,∴射线OC为∠MON的平分线.

答案： 1.
(1)[解]由作图过程可知,射线OC为∠MON 的平分线,故答案为平分线.
(2)[证明]由作图过程可得,OA=OB,AC=BC.在△AOC和△BOC中,OA=OB,OC=OC,AC=BC,
∴△AOC≌△BOC(SSS),
∴∠AOC=∠BOC,
∴射线OC为∠MON的平分线.

2分别画出已知钝角和平角的平分线.

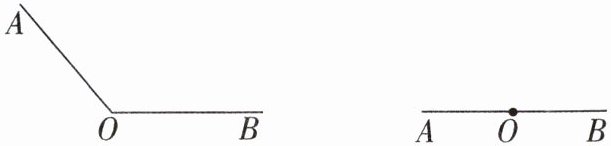
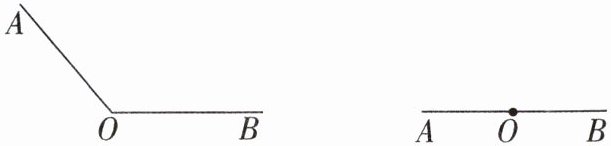
答案：
2.[解]如图所示，射线OC即为角平分线.
　　

3[2024广东广州期中]点P在$∠AOB$的平分线上,点P到OA边的距离等于6,点Q是OB边上的任意一点,则下列选项正确的是( )

A.$PQ＞6$
B.$PQ≥6$
C.$PQ＜6$
D.$PQ≤6$

答案：
3.B　[解析]如图,OP平分∠AOB,PM=6,PM⊥OA,过点P作PN⊥OB 于N,则PM=PN=6.
∵点Q是OB边上的任意一点,
∴PQ≥6.故选B.

4如图,已知$\triangle ABC$的周长是34,BO,CO分别平分$∠ABC和∠ACB$,$OD⊥BC$于D,且$OD= 4$,则$\triangle ABC$的面积是( )


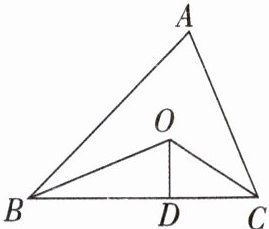
A.17
B.34
C.38
D.68

答案：
4.D　[解析]如图，过点O作OE⊥AB于E,OF⊥AC于F,连接OA.
∵BO,CO分别平分∠ABC 和∠ACB,OD⊥BC,
∴OE=OD,OD=OF,即OE=OF=OD=4,
∴△ABC的面积为S△AOB+S△AOC+S△OBC=$\frac{1}{2}$×AB×OE+$\frac{1}{2}$×AC×OF+$\frac{1}{2}$×BC×OD=$\frac{1}{2}$×4×(AB+AC+BC)=$\frac{1}{2}$×4×34=68.故选D.

如图,在平面直角坐标系中,以O为圆心,适当长为半径作弧,交x轴负半轴于点M,交y轴正半轴于点N,分别以点M,N为圆心,大于$\frac {1}{2}MN$的长为半径作弧,两弧在第二象限交于点P.若点P的坐标为$(a,b)$,则a与b的数量关系为(D)
A.$a= b$
B.$a-b= 1$
C.$a+b= -1$
D.$a+b= 0$

答案： 5.D　[解析]根据作图方法可得点P在第二象限的角平分线上,
∴点P到x轴、y轴的距离相等,
∴a=−b,
∴a+b=0,故选D.

6如图,点P是$∠AOB$的平分线OC上一点,$PN⊥OB$于点N,点M是线段ON上一点.已知$OM= 3,ON= 5$,点D为OA上一点,若满足$PD= PM$,则OD的长度为____.

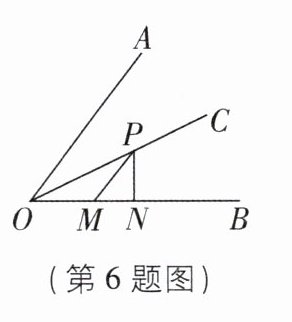
答案：
6.3或7　[解析]如图，过点P 作PE⊥OA于点E.
∵OC平分∠AOB,PE⊥OA,PN⊥OB,
∴PE=PN.
∵OP = OP,
∴Rt△OPE≌Rt△OPN(HL),
∴OE=ON=5.
∵OM=3,ON=5,
∴MN=2.若点D在线段OE 上,
∵PM=PD,PE=PN,
∴Rt△PMN≌Rt△PDE(HL),
∴DE=MN=2,
∴OD=OE−DE=3.若点D'在射线EA上,同理可得D'E=MN=2,
∴OD'=OE+D'E=7.故答案为3或7.

7[2025河南洛阳期中]如图,已知$∠AOB= α$,点C在$∠AOB$的平分线OP上,$∠DCE= 180^{\circ }-α$,且$∠DCE$的两边分别与OA,OB交于点D和点E,求证:$CD= CE$.

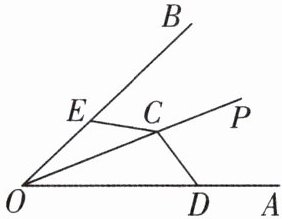
答案：
7.[证明]如图,过点C作CF⊥OA于点F,CG⊥OB于点G,则∠OFC=∠OGC=90°.

∵∠OFC+∠OGC+∠FOG+∠FCG=360°,
∴∠FOG+∠FCG=180°.
∵∠DCE=180°−α,∠AOB=α,
∴　∠DCE+∠AOB=180°,
∴∠FCG=∠DCE,即∠FCE+∠ECG=∠FCE+∠DCF,
∴∠ECG=∠DCF.又
∵OP为∠AOB的平分线,CF⊥OA,CG⊥OB,
∴CF=CG,
∴△CEG≌△CDF(ASA),
∴CD=CE.