第52页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1 [2024吉林松原题中]如图,平移图形①,与图形②可以拼成一个等边三角形,则图中∠α的度数是(
A.110°
B.120°
C.140°
D.150°
D
)A.110°
B.120°
C.140°
D.150°
答案:
D [解析]
∵可以拼成一个等边三角形,
∴∠A=∠B=60°,
∴∠α=540°−60°−60°−(180°−70°)−160°=150°.故选D.
∵可以拼成一个等边三角形,
∴∠A=∠B=60°,
∴∠α=540°−60°−60°−(180°−70°)−160°=150°.故选D.
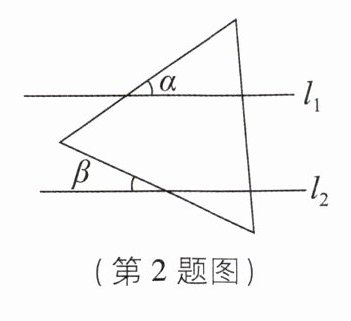
2 如图,直线$l_1//l_2,$将等边三角形如图放置.若∠α= 35°,则∠β等于( )
A.35°
B.30°
C.25°
D.15°

A.35°
B.30°
C.25°
D.15°
答案:
C [解析]如图,过点A作AD//l₁,则∠BAD=∠α=35°.
∵l₁//l₂,
∴AD//l₂,
∴∠DAC=∠β.
∵△ABC是等边三角形,
∴∠BAC=60°,
∴∠β=∠DAC=∠BAC−∠DAB=60°−35°=25°.故选C.

C [解析]如图,过点A作AD//l₁,则∠BAD=∠α=35°.
∵l₁//l₂,
∴AD//l₂,
∴∠DAC=∠β.
∵△ABC是等边三角形,
∴∠BAC=60°,
∴∠β=∠DAC=∠BAC−∠DAB=60°−35°=25°.故选C.

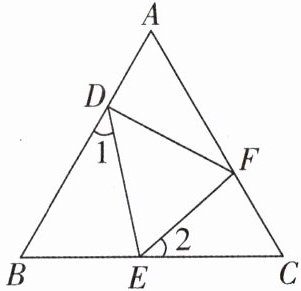
3 [2025辽宁大连期中]如图,△ABC是等边三角形,点D,E,F分别在AB,BC,AC上,∠1= ∠2,∠DFE= 70°,则∠EDF= ______°.

50
答案:
50 [解析]
∵△ABC是等边三角形,
∴∠A=∠B=∠C=60°.
∵∠DEC=∠2+∠DEF=∠1+∠B,∠1=∠2,
∴∠DEF=∠B=60°.
∵∠DFE=70°,
∴∠EDF=180°−∠DEF−∠DFE=180°−60°−70°=50°.故答案为50.
∵△ABC是等边三角形,
∴∠A=∠B=∠C=60°.
∵∠DEC=∠2+∠DEF=∠1+∠B,∠1=∠2,
∴∠DEF=∠B=60°.
∵∠DFE=70°,
∴∠EDF=180°−∠DEF−∠DFE=180°−60°−70°=50°.故答案为50.
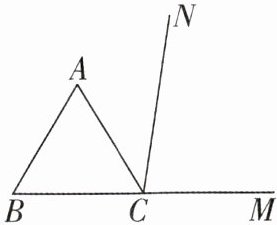
4 [2025福建南平期中]如图,CN是等边△ABC的外角∠ACM内部的一条射线,点A关于CN的对称点为D,连接BD,CD.
(1)依题意补全图形(尺规作图,保留作图痕迹,不写作法);
(2)若∠ACN= 40°,求∠BDC的度数.
(1)依题意补全图形(尺规作图,保留作图痕迹,不写作法);
(2)若∠ACN= 40°,求∠BDC的度数.

答案:
[解]
(1)如图所示.

(2)
∵A,D关于CN对称,
∴CN垂直平分AD,
∴AC=CD,
∴∠ACN=∠NCD=40°.
∵△ABC是等边三角形,
∴∠ACB=60°,AC=BC,
∴∠BCD=∠BCA+∠ACN+∠NCD=60°+2×40°=140°,BC=CD,
∴∠CBD=∠CDB,
∴∠BDC=$\frac{180^{\circ}-140^{\circ}}{2}$=20°.
[解]
(1)如图所示.

(2)
∵A,D关于CN对称,
∴CN垂直平分AD,
∴AC=CD,
∴∠ACN=∠NCD=40°.
∵△ABC是等边三角形,
∴∠ACB=60°,AC=BC,
∴∠BCD=∠BCA+∠ACN+∠NCD=60°+2×40°=140°,BC=CD,
∴∠CBD=∠CDB,
∴∠BDC=$\frac{180^{\circ}-140^{\circ}}{2}$=20°.
5 下列条件中,不能判定△ABC为等边三角形的是(
A.∠A= ∠B= 60°
B.∠B+∠C= 120°
C.∠B= 60°,AB= AC
D.∠A= 60°,AB= AC
B
)A.∠A= ∠B= 60°
B.∠B+∠C= 120°
C.∠B= 60°,AB= AC
D.∠A= 60°,AB= AC
答案:
B 【解析】
∵ ∠A=∠B=60°,
∴ ∠C=60°,
∴ ∠A=∠B=∠C,
∴ △ABC 是等边三角形,故选项 A 不符合题意
∵ ∠B+∠C=120°,
∴ ∠A=60°,
∴ △ABC 不一定是等边三角形,故选项 B 符合题意
∵ ∠B=60°,AB=AC,
∴ △ABC 是等边三角形,故选项 C 不符合题意
∵ ∠A=60°,AB=AC,
∴ △ABC 是等边三角形,故选项 D 不符合题意
∵ ∠A=∠B=60°,
∴ ∠C=60°,
∴ ∠A=∠B=∠C,
∴ △ABC 是等边三角形,故选项 A 不符合题意
∵ ∠B+∠C=120°,
∴ ∠A=60°,
∴ △ABC 不一定是等边三角形,故选项 B 符合题意
∵ ∠B=60°,AB=AC,
∴ △ABC 是等边三角形,故选项 C 不符合题意
∵ ∠A=60°,AB=AC,
∴ △ABC 是等边三角形,故选项 D 不符合题意
6 如图,一艘轮船由海平面上A地出发,向南偏西40°的方向行驶80海里到达B地,再由B地向北偏西20°的方向行驶80海里到达C地,则A,C两地相距(
A.100海里
B.80海里
C.60海里
D.40海里
B
)A.100海里
B.80海里
C.60海里
D.40海里
答案:
B [解析]连接AC.
∵点B在点A的南偏西40°方向上,点C在点B的北偏西20°方向上,
∴∠CBA=60°.又
∵BC=BA,
∴△ABC为等边三角形,
∴AC=BC=AB=80海里.故选B.
∵点B在点A的南偏西40°方向上,点C在点B的北偏西20°方向上,
∴∠CBA=60°.又
∵BC=BA,
∴△ABC为等边三角形,
∴AC=BC=AB=80海里.故选B.
在△ABC中,∠B= ∠C,若添加一个条件使△ABC是等边三角形,则添加的条件可以是
∠B=∠A
.(写出一个即可)
答案:
∠B=∠A(答案不唯一) [解析]当∠B=∠A 时,
∵∠B=∠C,
∴∠A=∠B=∠C,
∴△ABC 是等边三角形.故答案为∠B=∠A(答案不唯一).
∵∠B=∠C,
∴∠A=∠B=∠C,
∴△ABC 是等边三角形.故答案为∠B=∠A(答案不唯一).
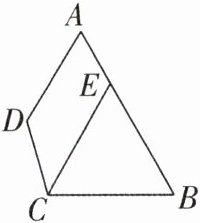
8 [2024吉林松原期中]如图,△ECB中,∠CEB= ∠B,延长BE至点A,过点A作AD//CE,∠A= 60°,连接CD.
求证:△ECB是等边三角形.
求证:△ECB是等边三角形.

答案:
[证明]
∵AD//CE,
∴∠A=∠CEB=60°.
∵∠CEB=∠B,
∴CE=CB,
∴△CEB是等腰三角形.又
∵∠CEB=60°,
∴△CEB是等边三角形.
∵AD//CE,
∴∠A=∠CEB=60°.
∵∠CEB=∠B,
∴CE=CB,
∴△CEB是等腰三角形.又
∵∠CEB=60°,
∴△CEB是等边三角形.
9 [2025吉林长春期中]如图,在四边形ABCD中,AB= AD,CB= CD,∠A= 60°,点E为AD上一点,连接BD,CE交于点F,CE//AB.
(1)判断△DEF的形状,并说明理由;
(2)若AD= 13,CE= 9,则CF的长为______.
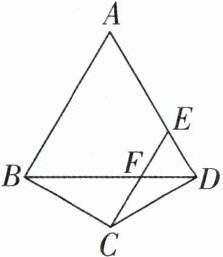
(1)判断△DEF的形状,并说明理由;
(2)若AD= 13,CE= 9,则CF的长为______.

答案:
[解]
(1)△DEF是等边三角形.理由如下:
∵AB=AD,∠A=60°,
∴△ABD为等边三角形,
∴∠ADB=∠ABD=60°.
∵CE//AB,
∴∠DEF=∠A=60°,∠EFD=∠ABD=60°,
∴∠EFD=∠EDF=∠DEF,
∴△DEF是等边三角形
(2)连接AC交BD于点O,如图.
∵AB=AD,CB=CD,
∴AC垂直平分BD,
∴AC平分∠BAD,
∴∠BAO=∠DAO.
∵CE//AB,
∴∠ACE=∠BAO=∠DAO,
∴AE=CE=9,
∴DE=AD−AE=13−9=4.
∵△DEF是等边三角形,
∴EF=DE=4,
∴CF=CE−EF=9−4=5.故答案为5.

[解]
(1)△DEF是等边三角形.理由如下:
∵AB=AD,∠A=60°,
∴△ABD为等边三角形,
∴∠ADB=∠ABD=60°.
∵CE//AB,
∴∠DEF=∠A=60°,∠EFD=∠ABD=60°,
∴∠EFD=∠EDF=∠DEF,
∴△DEF是等边三角形
(2)连接AC交BD于点O,如图.
∵AB=AD,CB=CD,
∴AC垂直平分BD,
∴AC平分∠BAD,
∴∠BAO=∠DAO.
∵CE//AB,
∴∠ACE=∠BAO=∠DAO,
∴AE=CE=9,
∴DE=AD−AE=13−9=4.
∵△DEF是等边三角形,
∴EF=DE=4,
∴CF=CE−EF=9−4=5.故答案为5.

查看更多完整答案,请扫码查看


