《2025年初中必刷题八年级数学上册人教版》

一、选择题(本大题共8小题,每小题5分,共40分)
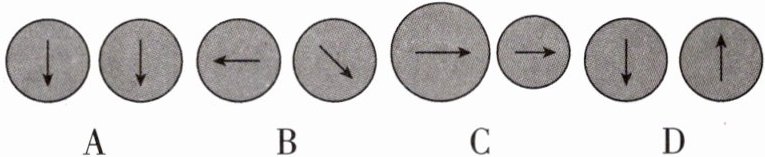
1 [2025安徽安庆质检]下列各选项中,两个图形不全等的是(C)

答案： C 【解析】A、B、D 选项,两个图形是全等图形,故选项不符合题意;C 选项,两个图形不是全等图形,故选项符合题意.故选 C.

2 [2025江苏南京质检]已知下图中的两个三角形全等,则$\angle 1$等于( )


A.$50^{\circ}$
B.$58^{\circ}$
C.$60^{\circ}$
D.$72^{\circ}$

答案：
B 【解析】如图,
∵△ABC 和△DEF 全等,AC=DF=b,DE=AB=a,
∴∠1=∠B,∠A=∠D=50°,∠F=∠C=72°,
∴∠1=180°-∠D-∠F=58°,故选 B.

3 [2025湖南长沙质检]如图,已知$\triangle ABC$,利用尺规作图的方法作出了$\triangle DEF$,请根据作图痕迹判断$\triangle ABC\cong\triangle DEF$的理论依据是(A)
A.$SAS$
B.$AAS$
C.$ASA$
D.$SSS$

答案： A 【解析】由作图可知,AC=DF,∠A=∠D,AB=DE,故△ABC≌△DEF(SAS).故选 A.

4 [2025甘肃张掖期末]如图,点$P为\angle AOB的平分线OC$上一点,$PM\perp OA于点M$,$PM= 6$,点$N为OB$上任意一点,则满足$PN= 6的点N$有( )


A.1个
B.2个
C.3个
D.4个

答案：
A 【解析】如图,过点 P 作 PN'⊥OB,交 OB于 N'.
∵OP 平分∠AOB,PM⊥OA,PN'⊥OB,
∴PN'=PM=6.由垂线段最短可知满足 PN=6 的点 N 有 1 个,即点 N'.故选 A.

5 [2025河北保定期中]如图,李师傅在四边形木板$ABCD$中裁下3个三角形(空白部分),已知$\angle B= \angle C= 90^{\circ}$,$AE\perp EF$,$AE= EF$,$\angle CGD= \angle EGF$,$AB= 30cm$,$BE= CD= 10cm$,$CG= 20cm$,则剩余木板(阴影部分)的面积为( )


A.$1600cm^{2}$
B.$1100cm^{2}$
C.$900cm^{2}$
D.$500cm^{2}$

答案：
B 【解析】如图,过点 F 作 FH⊥BC,则∠FHE=∠FHG=90°=∠B=∠C.
∵AE⊥EF,
∴∠AEF=90°,
∴∠BAE=∠FEH=90°-∠AEB. 在△ABE 和△EHF 中,$\left\{\begin{array}{l} ∠B=∠FHE,\\ ∠BAE=∠HEF,\\ AE=EF,\end{array}\right.$
∴△ABE≌△EHF(AAS),
∴EH=AB,FH=BE.
∵BE=CD,
∴FH=CD.在△FHG 和△DCG 中,$\left\{\begin{array}{l} ∠FGH=∠DGC,\\ ∠FHG=∠C,\\ FH=DC,\end{array}\right.$
∴△FHG≌△DCG(AAS),
∴HG=CG,
∴EG=EH+GH=AB+CG=50 cm,BC=BE+EG+CG=80 cm,
∴剩余木板(阴影部分)的面积为$S_{梯形ABCD}-S_{△ABE}-S_{△EFG}-S_{△DCG}=\frac{1}{2}(30+10)×80-\frac{1}{2}×30×10-\frac{1}{2}×50×10-\frac{1}{2}×20×10=1100(cm^{2})$,故选 B.

6 [2025广西玉林期中]如图所示,在$\triangle ABC$中,$\angle ABC= 70^{\circ}$,$BD平分\angle ABC$,$P为线段BD$上一动点,$Q为边AB$上一动点,当$AP+PQ$的值最小时,$\angle APD$的度数是( )


A.$55^{\circ}$
B.$60^{\circ}$
C.$65^{\circ}$
D.$70^{\circ}$

答案：
A 【解析】在 BC 上截取 BE=BQ,连接 PE,如图.
∵BD 平分∠ABC,
∴∠ABD=∠CBD=$\frac{1}{2}$∠ABC=35°.又
∵BP=BP,BQ=BE,
∴△PBQ≌△PBE(SAS),
∴PE=PQ,
∴AP+PQ=AP+PE,
∴当 A,P,E 在同一直线上,且 AE⊥BC 时,AP+PE 的值最小,即 AP+PQ 的值最小.
∵∠AEB=90°,∠ABE=70°,
∴∠BAE=90°-∠ABE=20°,
∴∠APD=∠BAP+∠ABP=20°+35°=55°,故选 A.
思路分析 在 BC 上截取 BE=BQ,连接 PE,证明△PBQ≌△PBE,得出 PE=PQ,则 AP+PQ=AP+PE,则当 A,P,E 在同一直线上,且 AE⊥BC 时,AP+PE 的值最小,即 AP+PQ 的值最小,再根据三角形内角和定理和三角形外角的性质,求出结果即可.

7 [2025江苏宿迁质检]如图,在长方形$ABCD$中,$E是边BC$的中点,$F在边AB$上,若$S_{\triangle DEF}= 5S_{\triangle BEF}= 10$,则$\frac{AB}{BF}$的值为( )


A.4
B.2
C.1.5
D.$\frac{5}{3}$

答案：
A 【解析】如图,延长 DE,AB交于点 G.
∵在长方形 ABCD中,AB//CD,AB=CD,
∴∠GBE=∠C.在△BEG 和△CED 中,$\left\{\begin{array}{l} ∠GBE=∠C,\\ BE=CE,\\ ∠BEG=∠CED,\end{array}\right.$
∴△BEG≌△CED(ASA),
∴DE=GE,BG=CD=AB,
∴$S_{△EGF}=S_{△DEF}=10$.
∵$5S_{△BEF}=10$,
∴$S_{△BEF}=2$,
∴$S_{△BEG}=S_{△FEG}-S_{△BEF}=8$,
∴$\frac{BG}{BF}=\frac{S_{△BEG}}{S_{△BEF}}=4$,
∴$\frac{AB}{BF}=\frac{BG}{BF}=4$,故选 A.

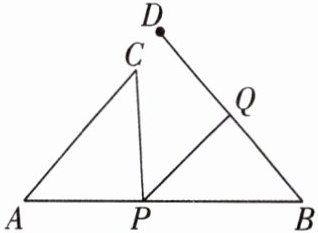
8 [2025浙江台州期中]如图,已知$AB= 10$,$AC= 6$,$BD= 8$,其中$\angle CAB= \angle DBA= \alpha$,点$P$以每秒2个单位长度的速度沿着$C\to A\to B$路径运动,同时,点$Q以每秒x个单位长度的速度沿着D\to B\to A$路径运动,一个点到达终点后另一个点立即停止运动,它们的运动时间为$t$秒.
①若$x= 1$,则点$P运动路程始终是点Q$运动路程的2倍；
②若$P$,$Q两点同时到达A$点,则$x= 5$；
③若$\alpha=90^{\circ}$,$t= 5$,$x= 1$,则$PC与PQ$垂直；
④若$\triangle ACP与\triangle BPQ$全等,则$x= \frac{4}{5}或\frac{4}{11}$.
以上说法正确的个数为( )


A.1
B.2
C.3
D.4

答案：
B 【解析】若 x=1,运动时间为 t 秒,则点 P运动路程为 2t,点 Q 运动路程为 t,故点 P 运动路程始终是点 Q 运动路程的 2 倍,故①正确,符合题意.点 P 到达点 A 的运动时间为 6÷2=3(秒),当 x=5 时,点 Q 到达点 A 的运动时间为(8+10)÷5=3.6(秒),3.6≠3,故②不正确,不符合题意.如图所示,当 t=5,x=1 时,点 P运动的路程为 2×5=10,点 Q 运动的路程为 5×1=5.
∵AC=6,DQ=5,BD=8,
∴AP=10-6=4,BQ=BD-DQ=8-5=3.
∵AB=10,
∴PB=AB-AP=10-4=6,
∴PB=CA.又
∵∠CAP=∠PBQ=90°,AP≠BQ,
∴△CAP 和△PBQ 不全等,
∴∠C≠∠QPB.
∵∠C+∠CPA=90°,
∴∠QPB+∠CPA≠90°,
∴∠CPQ=180°-(∠QPB+∠CPA)≠90°,
∴PC 与 PQ 不垂直,故③不正确,不符合题意.当点 P 在 AB 上,且点 Q 在 BD 上时,AP=2t-6,QD=xt,则 PB=10-(2t-6)=16-2t,BQ=8-xt.若△ACP 与△BPQ 全等,则 AC=PB 且 AP=BQ 或 AC=BQ 且 AP=BP,即 6=16-2t 且 2t-6=8-xt 或 6=8-xt 且 2t-6=16-2t,解得 x=$\frac{4}{5}$或$\frac{4}{11}$,故④正确,符合题意,故选 B.

二、填空题(本大题共3小题,每小题5分,共15分)
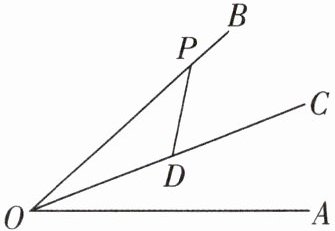
9 [2025北京大兴区期末]如图,$OC是\angle AOB$的平分线,点$D$,$P分别在射线OC和OB$上,$OD＞DP且\angle DPO= 36^{\circ}$,点$Q是射线OA$上的一点,若$DQ= DP$,则$\angle DQO$的度数为____.

答案：
36°或 144° 【解析】如图,过点 D 作 DH⊥OA于 H,DN⊥OB 于 N.
∵OD 平分∠AOB,DH⊥OA,DN⊥OB,
∴DH=DN.当点 Q 在点 H的右侧时,在 Rt△DPN 和 Rt△DQH 中,$\left\{\begin{array}{l} DP=DQ,\\ DN=DH,\end{array}\right.$
∴Rt△DPN≌Rt△DQH(HL),
∴∠DPO=∠DQO=36°.当点 Q 在点 H 左侧时,如点 Q',同理可得∠DQ'H=36°,
∴∠DQ'O=144°.综上所述,∠DQO 的度数为 36°或144°,故答案为 36°或 144°.