第54页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1 [2024 河南信阳期中] 如图,在 $ \triangle A B C $ 中,$ \angle C = 90 ^ { \circ } $,$ \angle B = 15 ^ { \circ } $,$ A B $ 的垂直平分线交 $ B C $ 于点 $ D $,交 $ A B $ 于点 $ E $。若 $ D B = 12 \mathrm { ~cm } $,则 $ A C = $( )
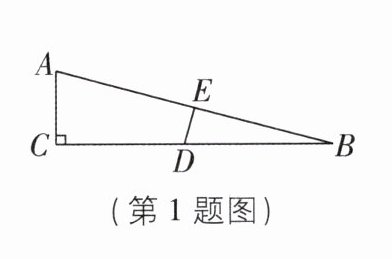
A.$ 4 \mathrm { ~cm } $
B.$ 5 \mathrm { ~cm } $
C.$ 6 \mathrm { ~cm } $
D.$ 7 \mathrm { ~cm } $

A.$ 4 \mathrm { ~cm } $
B.$ 5 \mathrm { ~cm } $
C.$ 6 \mathrm { ~cm } $
D.$ 7 \mathrm { ~cm } $
答案:
C 【解析】连接 AD,如图.
∵ DE 是 AB 的垂直平分线,
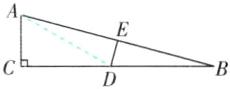
∴ AD=DB=12 cm,
∴ ∠DAE=∠B=15°.又
∵ ∠C=90°,
∴ ∠CAD=180°-∠C-∠B-∠DAE=60°,
∴ ∠ADC=30°.在直角三角形 ACD 中,AC=$\frac{1}{2}$AD=6 cm. 故选 C.
C 【解析】连接 AD,如图.
∵ DE 是 AB 的垂直平分线,

∴ AD=DB=12 cm,
∴ ∠DAE=∠B=15°.又
∵ ∠C=90°,
∴ ∠CAD=180°-∠C-∠B-∠DAE=60°,
∴ ∠ADC=30°.在直角三角形 ACD 中,AC=$\frac{1}{2}$AD=6 cm. 故选 C.
如图,在 $ \triangle A B C $ 中,$ \angle A : \angle B : \angle B C A = 1 : 2 : 3 $,$ C D \perp A B $ 于点 $ D $,$ A B = 12 $,则 $ D B $ 等于(
A.3
B.4
C.6
D.9
A
)A.3
B.4
C.6
D.9
答案:
A 【解析】
∵ 在△ABC 中,∠A:∠B:∠BCA=1:2:3,
∴ ∠ACB=90°,∠A=30°,∠B=60°.
∵ AB=12,
∴ BC=6.
∵ CD⊥AB,
∴ ∠BDC=90°,
∴ ∠BCD=30°,
∴ BD=3.
∵ 在△ABC 中,∠A:∠B:∠BCA=1:2:3,
∴ ∠ACB=90°,∠A=30°,∠B=60°.
∵ AB=12,
∴ BC=6.
∵ CD⊥AB,
∴ ∠BDC=90°,
∴ ∠BCD=30°,
∴ BD=3.
3 [2024 北京西城区期末] 如图,$ \mathrm { Rt } \triangle A B C $ 中,$ \angle A C B = 90 ^ { \circ } $,$ \angle B = 30 ^ { \circ } $,$ A C = 2 $。$ D $ 为 $ B C $ 上一动点,连接 $ A D $,$ A D $ 的垂直平分线分别交 $ A C $,$ A B $ 于点 $ E $,$ F $,则线段 $ B F $ 长的最大值是( )
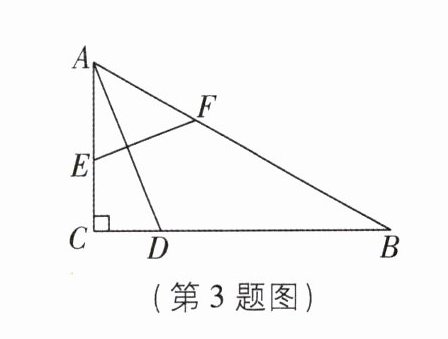
A.$ \frac { 1 } { 2 } $
B.$ \frac { 4 } { 3 } $
C.$ \frac { 8 } { 3 } $
D.4

A.$ \frac { 1 } { 2 } $
B.$ \frac { 4 } { 3 } $
C.$ \frac { 8 } { 3 } $
D.4
答案:
C 【解析】过点 F 作 FH⊥BC 于 H,连接 DF,如图.
∵ EF 垂直平分 AD,
∴ AF=DF.设 AF=DF=x.
∵ ∠B=30°,∠C=90°,AC=2,
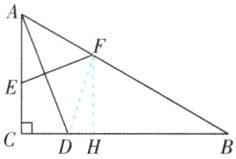
∴ AB=4,则 BF=4-x,
∴ FH=$\frac{1}{2}$BF=2-$\frac{1}{2}$x,
∴ x≥2-$\frac{1}{2}$x,解得 x≥$\frac{4}{3}$,
∴ AF 长的最小值为$\frac{4}{3}$,故 BF 长的最大值为 4-$\frac{4}{3}$=$\frac{8}{3}$. 故选 C.
C 【解析】过点 F 作 FH⊥BC 于 H,连接 DF,如图.
∵ EF 垂直平分 AD,
∴ AF=DF.设 AF=DF=x.
∵ ∠B=30°,∠C=90°,AC=2,

∴ AB=4,则 BF=4-x,
∴ FH=$\frac{1}{2}$BF=2-$\frac{1}{2}$x,
∴ x≥2-$\frac{1}{2}$x,解得 x≥$\frac{4}{3}$,
∴ AF 长的最小值为$\frac{4}{3}$,故 BF 长的最大值为 4-$\frac{4}{3}$=$\frac{8}{3}$. 故选 C.
4 [2025 黑龙江哈尔滨质检] 如图,一艘轮船以 15 海里/时的速度由南向北航行,在 $ A $ 处测得小岛 $ P $ 在北偏西 $ 15 ^ { \circ } $ 方向上,2 小时后,轮船在 $ B $ 处测得小岛 $ P $ 在北偏西 $ 30 ^ { \circ } $ 方向上,在小岛 $ P $ 周围 18 海里内有暗礁,若轮船继续向前航行,____触礁的危险。(填“有”或“无”)


答案:
有 【解析】如图,过点 P 作 PC⊥AB.
∵ ∠PBC=30°,∠PAB=15°,
∴ ∠APB=30°-15°=15°,
∴ ∠PAB=∠APB,

∴ PB=AB.
∵ AB=15×2=30(海里),
∴ PB=30 海里,
∴ PC=$\frac{1}{2}$PB=15 海里.
∵ 15<18,
∴ 有触礁的危险. 故答案为有.
有 【解析】如图,过点 P 作 PC⊥AB.
∵ ∠PBC=30°,∠PAB=15°,
∴ ∠APB=30°-15°=15°,
∴ ∠PAB=∠APB,

∴ PB=AB.
∵ AB=15×2=30(海里),
∴ PB=30 海里,
∴ PC=$\frac{1}{2}$PB=15 海里.
∵ 15<18,
∴ 有触礁的危险. 故答案为有.
5 如图,$ \angle M A N = 60 ^ { \circ } $,点 $ B $ 在射线 $ A M $ 上,且 $ A B = 2 $,点 $ C $ 在射线 $ A N $ 上。若 $ \triangle A B C $ 是锐角三角形,则 $ A C $ 的取值范围是____。


答案:
1<AC<4 【解析】如图,过点 B 作 BC₁⊥AN,垂足为 C₁,BC₂⊥AM,交 AN 于点 C₂.在 Rt△ABC₁ 中,

AB=2,∠A=60°,
∴ ∠ABC₁=30°,
∴ AC₁=$\frac{1}{2}$AB=1.在 Rt△ABC₂ 中,AB=2,∠A=60°,
∴ ∠AC₂B=30°,
∴ AC₂=2AB=4.当点 C 在 C₁ 和 C₂ 之间时,△ABC 是锐角三角形,
∴ AC 的取值范围是 1<AC<4. 故答案为 1<AC<4.
1<AC<4 【解析】如图,过点 B 作 BC₁⊥AN,垂足为 C₁,BC₂⊥AM,交 AN 于点 C₂.在 Rt△ABC₁ 中,

AB=2,∠A=60°,
∴ ∠ABC₁=30°,
∴ AC₁=$\frac{1}{2}$AB=1.在 Rt△ABC₂ 中,AB=2,∠A=60°,
∴ ∠AC₂B=30°,
∴ AC₂=2AB=4.当点 C 在 C₁ 和 C₂ 之间时,△ABC 是锐角三角形,
∴ AC 的取值范围是 1<AC<4. 故答案为 1<AC<4.
6 [2025 辽宁大连期末] 如图,在平面直角坐标系 $ x O y $ 中,已知点 $ A $ 的坐标是 $ ( 0,9 ) $,以 $ O A $ 为边在其右侧作等边三角形 $ O A A _ { 1 } $,过 $ A _ { 1 } $ 作 $ x $ 轴的垂线,垂足为点 $ O _ { 1 } $,以 $ O _ { 1 } A _ { 1 } $ 为边在其右侧作等边三角形 $ O _ { 1 } A _ { 1 } A _ { 2 } $,过点 $ A _ { 2 } $ 作 $ x $ 轴的垂线,垂足为点 $ O _ { 2 } $,以 $ O _ { 2 } A _ { 2 } $ 为边在其右侧作等边三角形 $ O _ { 2 } A _ { 2 } A _ { 3 } $,…$ $,按此规律继续作下去,得到等边三角形 $ O _ { 2025 } A _ { 2025 } A _ { 2026 } $,则点 $ A _ { 2025 } $ 的纵坐标为____

$9×\left(\frac{1}{2}\right)^{2025}$
。
答案:
$9×\left(\frac{1}{2}\right)^{2025}$ 【解析】
∵ 点 A 的坐标是(0,9),以 OA 为边在其右侧作等边三角形 OAA₁,过点 A₁ 作 x 轴的垂线,垂足为点 O₁,
∴ ∠A₁OO₁=90°-60°=30°,∠OO₁A₁=90°,OA₁=OA=9,
∴ O₁A₁=$\frac{1}{2}$OA₁=9×$\frac{1}{2}$,
∴ 点 A₁ 的纵坐标是 9×$\frac{1}{2}$.
∵ 以 O₁A₁ 为边在其右侧作等边三角形 O₁A₁A₂,过点 A₂ 作 x 轴的垂线,垂足为点 O₂,
∴ ∠A₂O₁O₂=90°-60°=30°,∠O₁O₂A₂=90°,O₁A₂=O₁A₁=9×$\frac{1}{2}$,
∴ O₂A₂=$\frac{1}{2}$O₁A₂=9×$\frac{1}{2}×\frac{1}{2}$,
∴ 点 A₂ 的纵坐标是 9×$\frac{1}{2}×\frac{1}{2}$,即$9×\left(\frac{1}{2}\right)^2$.
∵ 以 O₂A₂ 为边在其右侧作等边三角形 O₂A₂A₃,同理,得点 A₃ 的纵坐标是$9×\left(\frac{1}{2}\right)^3$,
∴ 根据规律可知点 A₂₀₂₅ 的纵坐标是$9×\left(\frac{1}{2}\right)^{2025}$. 故答案为$9×\left(\frac{1}{2}\right)^{2025}$.
∵ 点 A 的坐标是(0,9),以 OA 为边在其右侧作等边三角形 OAA₁,过点 A₁ 作 x 轴的垂线,垂足为点 O₁,
∴ ∠A₁OO₁=90°-60°=30°,∠OO₁A₁=90°,OA₁=OA=9,
∴ O₁A₁=$\frac{1}{2}$OA₁=9×$\frac{1}{2}$,
∴ 点 A₁ 的纵坐标是 9×$\frac{1}{2}$.
∵ 以 O₁A₁ 为边在其右侧作等边三角形 O₁A₁A₂,过点 A₂ 作 x 轴的垂线,垂足为点 O₂,
∴ ∠A₂O₁O₂=90°-60°=30°,∠O₁O₂A₂=90°,O₁A₂=O₁A₁=9×$\frac{1}{2}$,
∴ O₂A₂=$\frac{1}{2}$O₁A₂=9×$\frac{1}{2}×\frac{1}{2}$,
∴ 点 A₂ 的纵坐标是 9×$\frac{1}{2}×\frac{1}{2}$,即$9×\left(\frac{1}{2}\right)^2$.
∵ 以 O₂A₂ 为边在其右侧作等边三角形 O₂A₂A₃,同理,得点 A₃ 的纵坐标是$9×\left(\frac{1}{2}\right)^3$,
∴ 根据规律可知点 A₂₀₂₅ 的纵坐标是$9×\left(\frac{1}{2}\right)^{2025}$. 故答案为$9×\left(\frac{1}{2}\right)^{2025}$.
7 [2024 江西南昌期中] 如图,在 $ \triangle A B C $ 中,$ \angle A = 90 ^ { \circ } $,$ \angle B = 30 ^ { \circ } $,$ A C = 6 \mathrm { ~cm } $,点 $ D $ 从点 $ A $ 出发以 $ 1 \mathrm { ~cm } / \mathrm { s } $ 的速度向点 $ C $ 运动,同时点 $ E $ 从点 $ C $ 出发以 $ 2 \mathrm { ~cm } / \mathrm { s } $ 的速度向点 $ B $ 运动,运动的时间为 $ t \mathrm { ~s } $,解决以下问题:
(1)当 $ t $ 为何值时,$ \triangle D E C $ 为等边三角形?
(2)当 $ t $ 为何值时,$ \triangle D E C $ 为直角三角形?

(1)当 $ t $ 为何值时,$ \triangle D E C $ 为等边三角形?
(2)当 $ t $ 为何值时,$ \triangle D E C $ 为直角三角形?

答案:
【解】
(1)根据题意可得 AD=t cm,CD=(6-t)cm,CE=2t cm.
∵ ∠A=90°,∠B=30°,AC=6 cm,
∴ BC=2AC=12 cm,∠C=90°-∠B=90°-30°=60°.
∵ △DEC 为等边三角形,
∴ CD=CE,
∴ 6-t=2t,
∴ t=2,
∴ 当 t 的值为 2 时,△DEC 为等边三角形.
(2)①当∠DEC 为直角时,∠EDC=30°,
∴ CE=$\frac{1}{2}$DC,
∴ 2t=$\frac{1}{2}$(6-t),
∴ t=$\frac{6}{5}$;②当∠EDC 为直角时,∠DEC=30°,
∴ CD=$\frac{1}{2}$CE,
∴ 6-t=$\frac{1}{2}×$2t,
∴ t=3,
∴ 当 t 的值为$\frac{6}{5}$或 3 时,△DEC 为直角三角形.
(1)根据题意可得 AD=t cm,CD=(6-t)cm,CE=2t cm.
∵ ∠A=90°,∠B=30°,AC=6 cm,
∴ BC=2AC=12 cm,∠C=90°-∠B=90°-30°=60°.
∵ △DEC 为等边三角形,
∴ CD=CE,
∴ 6-t=2t,
∴ t=2,
∴ 当 t 的值为 2 时,△DEC 为等边三角形.
(2)①当∠DEC 为直角时,∠EDC=30°,
∴ CE=$\frac{1}{2}$DC,
∴ 2t=$\frac{1}{2}$(6-t),
∴ t=$\frac{6}{5}$;②当∠EDC 为直角时,∠DEC=30°,
∴ CD=$\frac{1}{2}$CE,
∴ 6-t=$\frac{1}{2}×$2t,
∴ t=3,
∴ 当 t 的值为$\frac{6}{5}$或 3 时,△DEC 为直角三角形.
查看更多完整答案,请扫码查看


