《2025年初中必刷题八年级数学上册人教版》

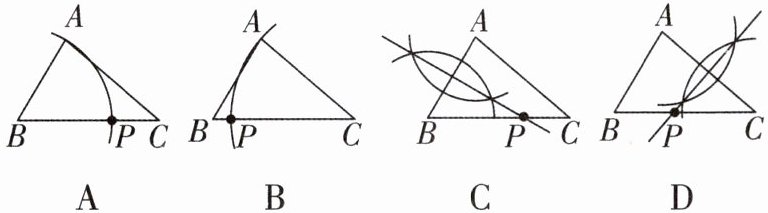
1 [2025 福建厦门期中]△ABC 中,AB＜AC＜BC,如果要用尺规作图的方法在 BC 上确定一点 P,使 PA+PB= BC,那么符合要求的作图痕迹是(D)

答案： D [解析]
∵PA+PB=BC,PC+PB=BC,
∴PA=PC,
∴点P在AC的垂直平分线上，即点P为AC的垂直平分线与BC的交点.故选D.

如图,在△ABC 中,分别以点 A 和点 B 为圆心,以相同的长(大于 $\frac{1}{2}AB$)为半径作弧,两弧相交于点 M 和点 N,作直线 MN 交 AB 于点 D,交 AC 于点 E,连接 CD。若△CDB 的面积为 24,△ADE 的面积为 18,则四边形 E DBC 的面积为______30。

答案： 由作法得MN垂直平分AB，
∴AD=BD，
∵△CDB的面积为24，
∴S△ADC=S△BDC=24，
∵△ADE的面积为18，
∴S△CDE=S△ADC-S△ADE=24-18=6，
∴四边形EDBC的面积=S△CDE+S△BCD=6+24=30。
故答案为30。

3 [2024 福建莆田期中]如图,在平面直角坐标系 xOy 中,点 A(0,8),点 B(6,8)。

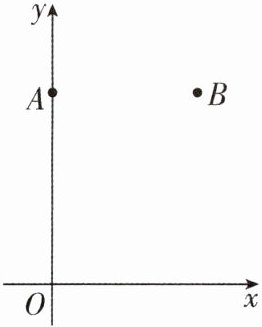
(1)尺规作图：在第一象限内求作一个点 P,使点 P 同时满足下列两个条件(要求保留作图痕迹,不必写出作法)。
①点 P 到 A,B 两点的距离相等；
②点 P 到两坐标轴的距离相等。
(2)(1)中点 P 的坐标为______。

答案：
【解】
(1)如图，点P即为所求.

(2)
∵点A(0,8),点B(6,8),
∴线段AB中点坐标为(3,8),
∴点P横坐标为3.
∵点P到两坐标轴的距离相等，点P在第一象限，
∴P(3,3).故答案为(3,3).

4 如图,网格中的△ABC 与△DEF 为轴对称图形。
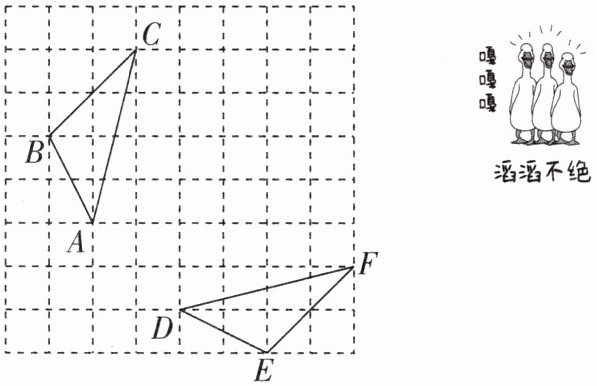
(1)利用网格线作出△ABC 与△DEF 的对称轴 l。
(2)若每一个小正方形的边长为 1,则△ABC 的面积为______。
(3)找出顶点在格点,以 BC 为一边且与△ABC 全等(不与△ABC 重合)的三角形,这样的三角形在网格内共能画出______个。

答案：
【解】
(1)如图，直线l即为所作.

(2)△ABC的面积为2×4−$\frac{1}{2}$×2×1−$\frac{1}{2}$×4×1−$\frac{1}{2}$×2×2=3.故答案为3.
(3)如图，△MBC即为以BC为一边且与△ABC全等(不与△ABC重合)的三角形，这样的三角形在网格内能画1个.故答案为1.

5 [2025 重庆渝中区质检]如图,Rt△ACB 中,∠ACB= 90°。

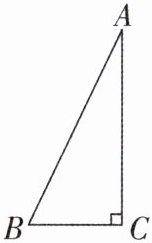
请在 AC 边上截取线段 CD,使得 CD= BC,过点 D 作直线 AB 的垂线,垂足为点 E,交 BC 的延长线于点 F。(尺规作图,保留作图痕迹,不写作法)

答案：
【解】如图.

6 [2025 山东泰安期中]如图,已知∠1 和线段 a,使用直尺和圆规作直角三角形,使得∠1 为其中的一个锐角,a 为直角三角形的斜边。(保留作图痕迹,不写作法)

答案：
【解】如图，Rt△ABC即为所求.