第11页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1 如图,点B,G,C在直线FE上,点D在线段AC上,则下列是△ADB的外角的是(
A.∠FBA
B.∠DBC
C.∠CDB
D.∠BDG
C
)A.∠FBA
B.∠DBC
C.∠CDB
D.∠BDG
答案:
C 【解析】∠CDB 是△ADB 的外角,故选 C.
2 [2025浙江杭州期末]一副直角三角板按如图所示方式叠放在一起,则图中∠α的度数是(
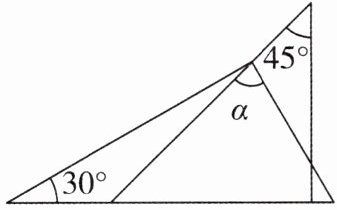
A.55°
B.60°
C.65°
D.75°
D
)
A.55°
B.60°
C.65°
D.75°
答案:
D 【解析】如图,由题意得∠1=90° - 60° = 30°,所以∠α = 45° + 30° = 75°,故选 D.
3 [2025河北石家庄期中]如图,三角形纸片沿过一个顶点的直线剪开后得到①②两个三角形纸片,则下列结论一定正确的是(
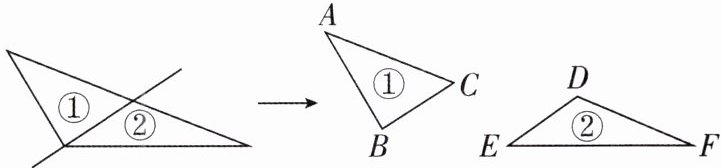
A.∠A = ∠E
B.∠C = ∠E
C.∠B = ∠E + ∠F
D.∠D = ∠A + ∠B
D
)
A.∠A = ∠E
B.∠C = ∠E
C.∠B = ∠E + ∠F
D.∠D = ∠A + ∠B
答案:
D 【解析】根据图形可知∠A 不一定等于∠E,∠C 不等于∠E,∠B 不一定等于∠E + ∠F。
∵∠D 相当于△ABC 的外角,
∴∠D = ∠A + ∠B,故选项 A、B、C 不符合题意,选项 D 符合题意,故选 D.
∵∠D 相当于△ABC 的外角,
∴∠D = ∠A + ∠B,故选项 A、B、C 不符合题意,选项 D 符合题意,故选 D.
4 [2024天津西青区期中]如图,点C是∠BAD内一点,连接CB,CD,∠A = 80°,∠B = 10°,∠D = 40°,则∠BCD的度数是(
A.110°
B.120°
C.130°
D.150°
C
)A.110°
B.120°
C.130°
D.150°
答案:
C 【解析】如图,延长 BC 交 AD 于 E。
∵∠BED 是△ABE 的一个外角,∠A = 80°,∠B = 10°,
∴∠BED = ∠A + ∠B = 90°。
∵∠BCD 是△CDE 的一个外角,
∴∠BCD = ∠BED + ∠D = 130°,故选 C.
∵∠BED 是△ABE 的一个外角,∠A = 80°,∠B = 10°,
∴∠BED = ∠A + ∠B = 90°。
∵∠BCD 是△CDE 的一个外角,
∴∠BCD = ∠BED + ∠D = 130°,故选 C.
5 如图,∠1,∠2,∠3是△ABC的3个外角,则∠1 + ∠2 + ∠3 =

360
°。
答案:
360 【解析】
∵三角形每个顶点处的内角与其外角之和为 180°,三角形的内角和为 180°,
∴∠1 + ∠2 + ∠3 = 3×180° - 180° = 360°,故答案为 360.
∵三角形每个顶点处的内角与其外角之和为 180°,三角形的内角和为 180°,
∴∠1 + ∠2 + ∠3 = 3×180° - 180° = 360°,故答案为 360.
6 如图,△ABC的内角∠ABC与外角∠ACE的平分线相交于点P,则∠A与∠P之间的数量关系是
∠P = $\frac{1}{2}$∠A
。
答案:
∠P = $\frac{1}{2}$∠A 【解析】
∵∠ACE 是△ABC 的一个外角,
∴∠A = ∠ACE - ∠ABC。
∵CP 是∠ACE 的平分线,
∴∠PCE = $\frac{1}{2}$∠ACE。
∵BP 是∠ABC 的平分线,
∴∠PBE = $\frac{1}{2}$∠ABC,
∴∠P = ∠PCE - ∠PBC = $\frac{1}{2}$×(∠ACE - ∠ABC) = $\frac{1}{2}$∠A,故答案为∠P = $\frac{1}{2}$∠A.
∵∠ACE 是△ABC 的一个外角,
∴∠A = ∠ACE - ∠ABC。
∵CP 是∠ACE 的平分线,
∴∠PCE = $\frac{1}{2}$∠ACE。
∵BP 是∠ABC 的平分线,
∴∠PBE = $\frac{1}{2}$∠ABC,
∴∠P = ∠PCE - ∠PBC = $\frac{1}{2}$×(∠ACE - ∠ABC) = $\frac{1}{2}$∠A,故答案为∠P = $\frac{1}{2}$∠A.
证法1:∵ ∠BAE,∠CBF,∠ACD是△ABC的三个外角,
∴
∴ ∠BAE + ∠CBF + ∠ACD = 2(∠1 + ∠2 + ∠3)。
∵
∴ ∠BAE + ∠CBF + ∠ACD = 360°。
证法2:∵平角等于 180°,∴∠BAE + ∠1 + ∠CBF + ∠2 + ∠ACD + ∠3 = 180°×3 = 540°,∴∠BAE + ∠CBF + ∠ACD = 540° - (∠1 + ∠2 + ∠3)。∵∠1 + ∠2 + ∠3 = 180°,∴∠BAE + ∠CBF + ∠ACD = 540° - 180° = 360°。
∴
∠BAE = ∠2 + ∠3,∠CBF = ∠1 + ∠3,∠ACD = ∠1 + ∠2
,∴ ∠BAE + ∠CBF + ∠ACD = 2(∠1 + ∠2 + ∠3)。
∵
∠1 + ∠2 + ∠3 = 180°
,∴ ∠BAE + ∠CBF + ∠ACD = 360°。
证法2:∵平角等于 180°,∴∠BAE + ∠1 + ∠CBF + ∠2 + ∠ACD + ∠3 = 180°×3 = 540°,∴∠BAE + ∠CBF + ∠ACD = 540° - (∠1 + ∠2 + ∠3)。∵∠1 + ∠2 + ∠3 = 180°,∴∠BAE + ∠CBF + ∠ACD = 540° - 180° = 360°。
答案:
【解】证法 1:
∵∠BAE,∠CBF,∠ACD 是△ABC 的三个外角,
∴∠BAE = ∠2 + ∠3,∠CBF = ∠1 + ∠3,∠ACD = ∠1 + ∠2,
∴∠BAE + ∠CBF + ∠ACD = 2(∠1 + ∠2 + ∠3)。
∵∠1 + ∠2 + ∠3 = 180°,
∴∠BAE + ∠CBF + ∠ACD = 360°。故答案为∠BAE = ∠2 + ∠3,∠CBF = ∠1 + ∠3,∠ACD = ∠1 + ∠2;∠1 + ∠2 + ∠3 = 180°。证法 2:
∵平角等于 180°,
∴∠BAE + ∠1 + ∠CBF + ∠2 + ∠ACD + ∠3 = 180°×3 = 540°,
∴∠BAE + ∠CBF + ∠ACD = 540° - (∠1 + ∠2 + ∠3)。
∵∠1 + ∠2 + ∠3 = 180°,
∴∠BAE + ∠CBF + ∠ACD = 540° - 180° = 360°.
∵∠BAE,∠CBF,∠ACD 是△ABC 的三个外角,
∴∠BAE = ∠2 + ∠3,∠CBF = ∠1 + ∠3,∠ACD = ∠1 + ∠2,
∴∠BAE + ∠CBF + ∠ACD = 2(∠1 + ∠2 + ∠3)。
∵∠1 + ∠2 + ∠3 = 180°,
∴∠BAE + ∠CBF + ∠ACD = 360°。故答案为∠BAE = ∠2 + ∠3,∠CBF = ∠1 + ∠3,∠ACD = ∠1 + ∠2;∠1 + ∠2 + ∠3 = 180°。证法 2:
∵平角等于 180°,
∴∠BAE + ∠1 + ∠CBF + ∠2 + ∠ACD + ∠3 = 180°×3 = 540°,
∴∠BAE + ∠CBF + ∠ACD = 540° - (∠1 + ∠2 + ∠3)。
∵∠1 + ∠2 + ∠3 = 180°,
∴∠BAE + ∠CBF + ∠ACD = 540° - 180° = 360°.
8 在△ABC中,∠ABC = 30°,∠BAC = 100°,BD平分∠ABC交AC于点D,点P为边AC上一点,PO ⊥ BD,垂足为O,则∠APO的度数为______
25°或 155°
。
答案:
25°或 155° 【解析】如图。
∵BD 平分∠ABC,
∴∠ABD = $\frac{1}{2}$∠ABC = 15°。当点 P 在线段 CD 上时,
∵∠PDO = ∠ADB = 180° - ∠A - ∠ABD = 180° - 100° - 15° = 65°,OP⊥BD,
∴∠POD = 90°,
∴∠APO = 90° - 65° = 25°;当点 P 在线段 AD 上时,如点 P',∠AP'O' = ∠P'O'D + ∠P'DO' = 90° + 65° = 155°,故答案为 25°或 155°.
∵BD 平分∠ABC,
∴∠ABD = $\frac{1}{2}$∠ABC = 15°。当点 P 在线段 CD 上时,
∵∠PDO = ∠ADB = 180° - ∠A - ∠ABD = 180° - 100° - 15° = 65°,OP⊥BD,
∴∠POD = 90°,
∴∠APO = 90° - 65° = 25°;当点 P 在线段 AD 上时,如点 P',∠AP'O' = ∠P'O'D + ∠P'DO' = 90° + 65° = 155°,故答案为 25°或 155°.
查看更多完整答案,请扫码查看


