《2025年初中必刷题八年级数学上册人教版》

1 [中] 把一张长方形纸片按图(1)、图(2)的方式从右向左连续对折两次后得到图(3),再在图(3)中挖去一个如图所示的三角形小孔,则重新展开后得到的图形是 (C)

答案： C 【解析】先由轴对称的定义，判断每条虚线两侧的图形是否成轴对称，由此得 C，D 两项满足，但 D 选项的基本图形的◇位置与题意不符，故选 C.

2 [2024 辽宁本溪期中,中] 如图,△ABC 中,D 点在 BC 上,分别以 AB,AC 所在直线为对称轴,画出点 D 的对称点 E,F,并连接 DE,DF. 根据图中标示的数据,求得∠EDF 的度数为 ( )

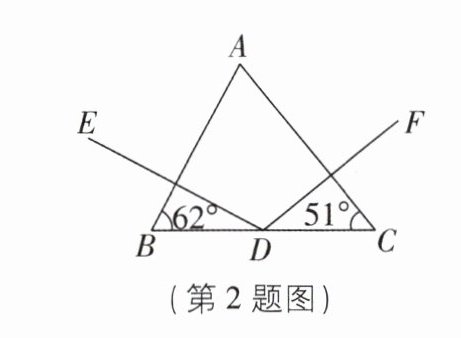
A.113°
B.124°
C.102°
D.134°

答案：
A 【解析】如图，设 AB 与 ED 交于点 M，AC 与 DF 交于点 N.
∵ 分别以 AB，AC 所在直线为对称轴，画出点 D 的对称点 E，F，$\therefore AB⊥ED$，$AC⊥DF$，$\therefore ∠BMD=∠DNC=90^{\circ }$. 在$Rt\triangle BDM$中，$∠ABD=62^{\circ }$，$\therefore ∠BDM=90^{\circ }-∠ABD=90^{\circ }-62^{\circ }=28^{\circ }$. 在$Rt\triangle CDN$中，$∠ACD=51^{\circ }$，$\therefore ∠CDN=90^{\circ }-∠ACD=90^{\circ }-51^{\circ }=39^{\circ }$，$\therefore ∠EDF=180^{\circ }-∠BDM-∠CDN=180^{\circ }-28^{\circ }-39^{\circ }=113^{\circ }$. 故选 A.
　　　　　　　　

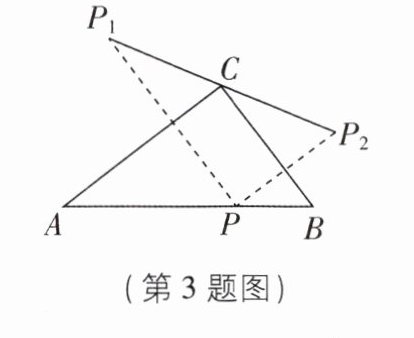
3 [中] 如图,在△ABC 中,∠ACB = 90°,BC = 6,AC = 8,AB = 10,动点 P 在边 AB 上运动 (不与端点重合),点 P 关于直线 AC,BC 对称的点分别为$ P_1,P_2,$则在点 P 的运动过程中,线段$ P_1P_2 $的长的最小值是______.

答案：
9.6
思路分析：利用轴对称的性质解决最值问题
连接 CP. 点 P 关于直线 AC，BC 对称的点分别为$P_{1}$，$P_{2}$，$CP_{1}=CP=CP_{2}$；$∠P_{1}CA=∠PCA$，$∠P_{2}CB=∠PCB$，$P_{1}$，C，$P_{2}$三点共线，$P_{1}P_{2}=2CP$，求 CP 的最小值，由垂线段最短，转化为求 AB 边上的高，利用$S_{Rt\triangle ABC}=\frac{1}{2}AB\cdot CP=\frac{1}{2}AC\cdot BC$，且$AB = 10$，$AC = 8$，$BC = 6$.
【解析】如图，连接 CP.
∵ 点 P 关于直线 AC，BC 对称的点分别为$P_{1}$，$P_{2}$，$\therefore P_{1}C=PC=P_{2}C$，$∠P_{1}CA=∠PCA$，$∠P_{2}CB=∠PCB$，$\therefore ∠P_{1}CP_{2}=2∠ACB=180^{\circ }$，$\therefore P_{1}$，C，$P_{2}$三点共线，$\therefore P_{1}P_{2}=2CP$. 当$CP⊥AB$时，CP 的长最小，此时线段$P_{1}P_{2}$的长最小.
∵$∠ACB = 90^{\circ }$，$BC = 6$，$AC = 8$，$AB = 10$，$\therefore CP=\frac{AC×BC}{AB}=4.8$，$\therefore $线段$P_{1}P_{2}$的长的最小值是 9.6.
　　　　　　　　　　

4 [2025 湖北武汉校级期中,较难] 已知点 A₀(-1,3),记 A₀ 关于直线 m (直线 m 上各点的横坐标都为 0) 的对称点为$ A_1,A_1 $关于直线 n (直线 n 上各点的纵坐标都为 1) 的对称点为$ A_2,A_2 $关于直线 p (直线 p 上各点的横坐标都为 -2) 的对称点为$ A_3,A_3 $关于直线 q (直线 q 上各点的纵坐标都为 3) 的对称点为$ A_4,A_4 $关于直线 m 的对称点为$ A_5,A_5 $关于直线 n 的对称点为$ A_6,…,$依此规律$,A_2₀_2_3 $的坐标是______(-2025,-2021).

答案： (-2025,-2021) 【解析】
∵ 直线 m 上各点的横坐标都为 0，$\therefore $直线 m 为直线$x = 0$，$\therefore $点$A_{0}(-1,3)$关于直线 m 的对称点为$A_{1}(1,3)$，在第一象限.
∵ 直线 n 上各点的纵坐标都为 1，$\therefore $直线 n 为直线$y = 1$，$\therefore $点$A_{1}(1,3)$关于直线$y = 1$的对称点为$A_{2}(1,-1)$，在第四象限.
∵ 直线 p 上各点的横坐标都为 -2，$\therefore $直线 p 为直线$x = -2$，$\therefore $点$A_{2}(1,-1)$关于直线$x = -2$的对称点为$A_{3}(-5,-1)$，在第三象限.
∵ 直线 q 上各点的纵坐标都为 3，$\therefore $直线 q 为直线$y = 3$，$\therefore $点$A_{3}(-5,-1)$关于直线$y = 3$的对称点为$A_{4}(-5,7)$，在第二象限.
∵$A_{4}(-5,7)$与$A_{5}$关于直线 m（即直线$x = 0$）对称，$\therefore A_{5}(5,7)$，在第一象限.
∵$A_{5}(5,7)$与$A_{6}$关于直线 n（即直线$y = 1$）对称，$\therefore A_{6}(5,-5)$，在第四象限.
∵$A_{6}(5,-5)$与$A_{7}$关于直线 p（即直线$x = -2$）对称，$\therefore A_{7}(-9,-5)$，在第三象限. …，按此规律，每四个点所在象限为一个循环.
∵$2023 = 4×505 + 3$，$\therefore $点$A_{2023}$与点$A_{3}$在同一象限. 又
∵$A_{3}(-5,-1)$，$A_{7}(-9,-5)$，…，
∴ 第三象限的点$A_{n}$坐标的特征为横坐标为$-(n + 2)$，纵坐标为$-(n - 2)$，$\therefore $点$A_{2023}$的横坐标为$-(2023 + 2)= -2025$，纵坐标为$-(2023 - 2)= -2021$，$\therefore A_{2023}$的坐标是$(-2025,-2021)$.

(1) ①已知点 A 坐标为 (2,1),则点 A 作相应变换后的点的坐标为(1,2)；
②若点 Q 作相应变换后的点的坐标为 (-1,2),求点 Q 的坐标.(2,-1)或(-1,-4)
(2) 已知 B(m,1),C(m,3).
①若线段 BC 上所有的点通过变换 2 所得图形在 x 轴下方,则 m 的取值范围是-1≤m＜1/2；
②如图,已知边长为 8 的正方形中心为点 O,且各边与坐标轴平行,若正方形内部 (含边) 同时存在线段 BC 上点的两种变换点,则 m 的取值范围是-4/3≤m＜-1或1＜m≤3.

答案： 【解】
(1)①
∵ 点 A 坐标为$(2,1)$，$2＞1$，
∴ 点 A 作变换 1 后的点的坐标为$(1,2)$，故答案为$(1,2)$.
②若点 Q 作变换 1 后的点的坐标为$(-1,2)$，则点 Q 的坐标为$(2,-1)$；若点 Q 作变换 2 后的点的坐标为$(-1,2)$，则两点关于直线$y = -1$对称，
∴ 点 Q 的坐标为$(-1,-4)$. 故点 Q 的坐标为$(2,-1)$或$(-1,-4)$.
(2)
∵$B(m,1)$，$C(m,3)$，
∴ 设线段 BC 上的点为$M(m,n)$，则$1\leqslant n\leqslant 3$，$M(m,n)$关于直线$y = m$的对称点的坐标为$(m,2m - n)$.
①
∵ 点$(m,n)$作变换 2，$\therefore |n|\geqslant |m|$，$\therefore -1\leqslant m\leqslant 1$.
∵ 线段 BC 上所有的点通过变换 2 所得图形在 x 轴下方，$\therefore 2m - n＜0$.
∵ n 的最小值为 1，$\therefore 2m＜1$，即$m＜\frac{1}{2}$，$\therefore -1\leqslant m＜\frac{1}{2}$. 故答案为$-1\leqslant m＜\frac{1}{2}$.
②
∵ 正方形内部（含边）同时存在线段 BC 上点的两种变换点，则线段 BC 与第二、四象限的角平分线或第一、三象限的角平分线有交点，$\therefore -3\leqslant m＜-1$或$1＜m\leqslant 3$. 当$M(m,n)$在第二、四象限的角平分线上时，$n = -m$. M 经过变换 2 得到的点在直线$y = -4$上时，$n - m=m-(-4)$，$\therefore n = 2m + 4$. 又
∵$n = -m$，$\therefore m = -\frac{4}{3}$，$\therefore -\frac{4}{3}\leqslant m＜-1$. 综上所述，$-\frac{4}{3}\leqslant m＜-1$或$1＜m\leqslant 3$. 故答案为$-\frac{4}{3}\leqslant m＜-1$或$1＜m\leqslant 3$.