第72页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1[中]小亮在计算$(6x^{3}y-3x^{2}y^{2})÷(3xy)$时,错把括号内的减号写成了加号,那么正确结果与错误结果的乘积是(
A.$2x^{2}-xy$
B.$2x^{2}+xy$
C.$4x^{4}-x^{2}y^{2}$
D.无法计算
C
)A.$2x^{2}-xy$
B.$2x^{2}+xy$
C.$4x^{4}-x^{2}y^{2}$
D.无法计算
答案:
C 【解析】正确结果:原式=(6x³y)÷(3xy)-(3x²y²)÷(3xy)=2x² - xy;错误结果:原式=(6x³y)÷(3xy)+(3x²y²)÷(3xy)=2x²+xy,
∴(2x² - xy)(2x²+xy)=4x⁴+2x³y - 2x³y - x²y²=4x⁴ - x²y².故选 C.
∴(2x² - xy)(2x²+xy)=4x⁴+2x³y - 2x³y - x²y²=4x⁴ - x²y².故选 C.
如图,对于任意正整数$n$,按流程图的计算方式,得到的结果(
A.随$n$的变化而变化
B.不变,总是0
C.不变,总是1
D.不变,总是2
D
)A.随$n$的变化而变化
B.不变,总是0
C.不变,总是1
D.不变,总是2
答案:
D 【解析】由题意可得(n²+2n)÷n - n=n + 2 - n=2,得到的结果不变,总是2.故选 D.
3[中]如图,一窗框由一个长方形和一个半圆组成,若要把窗框形状设计成 一个新的长方形,面积保持不变,且新窗框的底边长仍为$a$,则高度应为
一个新的长方形,面积保持不变,且新窗框的底边长仍为$a$,则高度应为
 一个新的长方形,面积保持不变,且新窗框的底边长仍为$a$,则高度应为
一个新的长方形,面积保持不变,且新窗框的底边长仍为$a$,则高度应为$b+\frac{1}{8}\pi a$
.
答案:
设新窗框的高度为$x$。根据题意,得$ab+\frac{1}{2}\pi\cdot\left(\frac{a}{2}\right)^2=ax$,$\therefore x=\left[ab+\frac{1}{2}\pi\cdot\left(\frac{a}{2}\right)^2\right]÷ a=\left(ab+\frac{1}{8}\pi a^2\right)÷ a=b+\frac{1}{8}\pi a$。
$b+\frac{1}{8}\pi a$
$b+\frac{1}{8}\pi a$
(1)根据上面各式的规律填空:
①$(x^{2022}-1)÷(x-1)=$
②$(x^{n}-1)÷(x-1)=$
(2)求$2^{2022}+2^{2021}+... +2+1$的值.
(3)若$1+x+x^{2}+... +x^{2021}= 0$,求$x^{2022}$的值.
①$(x^{2022}-1)÷(x-1)=$
$x^{2021}+x^{2020}+…+x+1$
;②$(x^{n}-1)÷(x-1)=$
$x^{n-1}+x^{n-2}+…+x+1$
.($n$为正整数)(2)求$2^{2022}+2^{2021}+... +2+1$的值.
【解】∵$(x^{n}-1)÷(x-1)=x^{n-1}+x^{n-2}+…+x+1$,∴$2^{2022}+2^{2021}+…+2+1=(2^{2023}-1)÷(2-1)=2^{2023}-1$.
(3)若$1+x+x^{2}+... +x^{2021}= 0$,求$x^{2022}$的值.
【解】∵$(x^{2022}-1)÷(x-1)=x^{2021}+x^{2020}+…+x+1=0$,∴$(x^{2022}-1)÷(x-1)=0$,∴$x^{2022}-1=0$,∴$x^{2022}=1$.
答案:
(1)①x²⁰²¹+x²⁰²⁰+…+x+1 ②xⁿ⁻¹+xⁿ⁻²+…+x+1
【解】
(2)
∵(xⁿ - 1)÷(x - 1)=xⁿ⁻¹+xⁿ⁻²+…+x+1,
∴2²⁰²²+2²⁰²¹+…+2+1=(2²⁰²³ - 1)÷(2 - 1)=2²⁰²³ - 1.
(3)
∵(x²⁰²² - 1)÷(x - 1)=x²⁰²¹+x²⁰²⁰+…+x+1=0,
∴(x²⁰²² - 1)÷(x - 1)=0,
∴x²⁰²² - 1=0,
∴x²⁰²²=1.
(1)①x²⁰²¹+x²⁰²⁰+…+x+1 ②xⁿ⁻¹+xⁿ⁻²+…+x+1
【解】
(2)
∵(xⁿ - 1)÷(x - 1)=xⁿ⁻¹+xⁿ⁻²+…+x+1,
∴2²⁰²²+2²⁰²¹+…+2+1=(2²⁰²³ - 1)÷(2 - 1)=2²⁰²³ - 1.
(3)
∵(x²⁰²² - 1)÷(x - 1)=x²⁰²¹+x²⁰²⁰+…+x+1=0,
∴(x²⁰²² - 1)÷(x - 1)=0,
∴x²⁰²² - 1=0,
∴x²⁰²²=1.
5[2025贵州毕节期末,中]如图,某新建高铁站前有一块长$(4a+3b)m$、宽$(3a+4b)m$的长方形空地,现计划在空地中间建一个长方形喷泉池(图中阴影部分),喷泉池四周是宽度均为$bm$的人行通道.
(1)求喷泉池的占地面积(用含$a,b$的代数式表示).
(2)喷泉池建成后,需给人行通道铺上地砖以方便旅客通行,若每块地砖的面积是$\frac {1}{13}b^{2}m^{2}$,则刚好铺满(既不重叠又无缝隙)时,需要多少块这样的地砖?
(1)求喷泉池的占地面积(用含$a,b$的代数式表示).
(2)喷泉池建成后,需给人行通道铺上地砖以方便旅客通行,若每块地砖的面积是$\frac {1}{13}b^{2}m^{2}$,则刚好铺满(既不重叠又无缝隙)时,需要多少块这样的地砖?

答案:
【解】
(1)喷泉池的占地面积为(4a+3b - 2b)·(3a+4b - 2b)=(4a+b)(3a+2b)=(12a²+11ab+2b²)m².
(2)[(4a+3b)(3a+4b)-(12a²+11ab+2b²)]÷($\frac{1}{13}$b)=(12a²+25ab+12b²-12a²-11ab-2b²)÷($\frac{1}{13}$b)=(14ab+10b²)÷($\frac{1}{13}$b)=(14ab)÷($\frac{1}{13}$b)+(10b²)÷($\frac{1}{13}$b)=(182a+130b)块.
答:需要(182a+130b)块这样的地砖.
(1)喷泉池的占地面积为(4a+3b - 2b)·(3a+4b - 2b)=(4a+b)(3a+2b)=(12a²+11ab+2b²)m².
(2)[(4a+3b)(3a+4b)-(12a²+11ab+2b²)]÷($\frac{1}{13}$b)=(12a²+25ab+12b²-12a²-11ab-2b²)÷($\frac{1}{13}$b)=(14ab+10b²)÷($\frac{1}{13}$b)=(14ab)÷($\frac{1}{13}$b)+(10b²)÷($\frac{1}{13}$b)=(182a+130b)块.
答:需要(182a+130b)块这样的地砖.
6核心素养运算能力[难]我们已经学习过多项式除以单项式,多项式除以多项式一般可用竖式计算.
例如:计算(6x^{4}-7x^{3}-x^{2}-1)÷(2x+1),可用竖式计算如下:
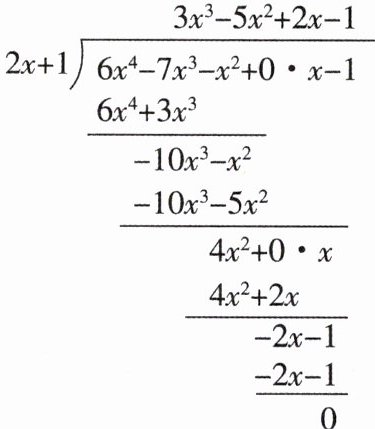
所以6x^{4}-7x^{3}-x^{2}-1除以2x + 1,商式为3x^{3}-5x^{2}+2x - 1,余式为0.根据上述材料,请回答下列问题:(1)(x^{3}-4x^{2}+7x-5)÷(x-2)的商式是____,余式是____.(2)x^{3}-x^{2}+ax + b能被x^{2}+2x + 2整除,求a,b的值.
例如:计算(6x^{4}-7x^{3}-x^{2}-1)÷(2x+1),可用竖式计算如下:
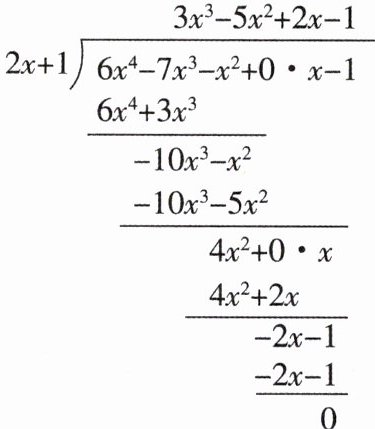
所以6x^{4}-7x^{3}-x^{2}-1除以2x + 1,商式为3x^{3}-5x^{2}+2x - 1,余式为0.根据上述材料,请回答下列问题:(1)(x^{3}-4x^{2}+7x-5)÷(x-2)的商式是____,余式是____.(2)x^{3}-x^{2}+ax + b能被x^{2}+2x + 2整除,求a,b的值.
答案:
【解】
(1)由题意,得

故答案为x² - 2x+3,1.
(2)由题意,得

∴a - 2=-6,b=-6,即a=-4,b=-6.
【解】
(1)由题意,得

故答案为x² - 2x+3,1.
(2)由题意,得

∴a - 2=-6,b=-6,即a=-4,b=-6.
查看更多完整答案,请扫码查看


