《2025年初中必刷题八年级数学上册人教版》

1 [2024山东烟台期中,中]如图是可调躺椅示意图,AE与BD的交点为C,∠CAB = 50°,∠CBA = 60°,∠CEF = 30°,∠D的大小可以调整。为了舒适,需使∠EFD = 130°,且∠CAB,∠CBA,∠E的度数保持不变,则∠D应调整为(D)



A.10°
B.20°
C.25°
D.30°

答案： D 【解析】连接 CF 并延长至点 M，如图所示。在△ABC 中，∠BAC = 50°，∠ABC = 60°，
∴∠ACB = 180° - ∠CAB - ∠CBA = 180° - 50° - 60° = 70°，
∴∠DCE = ∠ACB = 70°。
∵∠DFM = ∠DCF + ∠D，∠EFM = ∠ECF + ∠E，
∴∠EFD = ∠DCF + ∠ECF + ∠D + ∠E = ∠DCE + ∠D + ∠E，即 130° = 70° + ∠D + 30°，
∴∠D = 30°，故选 D.

如图,在△ABC中,∠ABC = 2∠C,点E,F分别在边BC,AC上,∠FEC = 28°,∠AEF = 2∠AFE,∠ABC的平分线与∠AEF的平分线交于点P,则∠P的度数为(B)
A.62°
B.56°
C.76°
D.58°

答案： B 【解析】
∵∠ABC = 2∠C，BP 平分∠ABC，
∴∠PBC = ∠C。设∠C = x，则∠PBC = x。
∵∠FEC = 28°，
∴∠AFE = x + 28°。
∵∠AEF = 2∠AFE，
∴∠AEF = 2x + 56°。
∵EP 平分∠AEF，
∴∠FEP = x + 28°。
∵∠PEC = ∠P + ∠PBC，
∴x + 28° + 28° = ∠P + x，
∴∠P = 56°，故选 B.

3 [2024河北承德期末,中]如图,已知点P是射线ON上一动点(不与点O重合),∠O = 30°,若△AOP为钝角三角形,则∠A的取值范围是0° ＜ ∠A ＜ 60°或 90° ＜ ∠A ＜ 150°。

答案： 0° ＜ ∠A ＜ 60°或 90° ＜ ∠A ＜ 150° 【解析】由题意，分两种情况：若∠A 为钝角，则 90° ＜ ∠A ＜ 180° - 30°，即 90° ＜ ∠A ＜ 150°。若∠A 为锐角，则 0° ＜ ∠A ＜ 90°，90° ＜ ∠APO ＜ 180° - 30°，即 90° ＜ ∠APO ＜ 150°，
∴30° ＜ ∠APN ＜ 90°。
∵∠APN = ∠O + ∠A，
∴30° ＜ ∠A + 30° ＜ 90°，
∴0° ＜ ∠A ＜ 60°。综上，∠A 的取值范围为 0° ＜ ∠A ＜ 60°或 90° ＜ ∠A ＜ 150°.

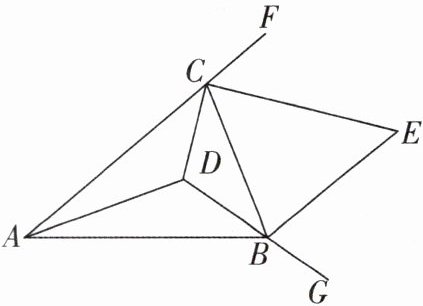
4 [2025浙江宁波期中,中]如图,在△ABC中,三个内角的平分线交于点D,其中∠CAB = n°,∠CBA = m°,延长AC至点F,延长DB至点G,∠FCB与∠CBG的平分线交于点E,若BE // AC,则$\frac{4}{7}n + \frac{3}{7}m = $$\frac{360}{7}$。

答案： $\frac{360}{7}$ 【解析】
∵BD 平分∠CBA，且∠CBA = m°，
∴∠CBD = $\frac{1}{2}$∠CBA = $\frac{1}{2}$m°。
∵延长 DB 至点 G，
∴∠CBD + ∠CBG = 180°，
∴∠CBG = 180° - ∠CBD = 180° - $\frac{1}{2}$m°。
∵BE 平分∠CBG，
∴∠CBE = $\frac{1}{2}$∠CBG = $\frac{1}{2}$(180° - $\frac{1}{2}$m°) = 90° - $\frac{1}{4}$m°。
∵延长 AC 至点 F，
∴∠FCB 是△ABC 的外角，
∵∠CAB = n°，∠CBA = m°，
∴∠FCB = ∠CBA + ∠CAB = m° + n°。又
∵BE//AC，
∴∠FCB + ∠CBE = 180°，
∴m° + n° + 90° - $\frac{1}{4}$m° = 180°，
∴$\frac{3}{4}$m + n = 90°，
∴$\frac{4}{7}$n + $\frac{3}{7}$m = $\frac{4}{7}$(n + $\frac{3}{4}$m) = $\frac{4}{7}$×90 = $\frac{360}{7}$，故答案为$\frac{360}{7}$.

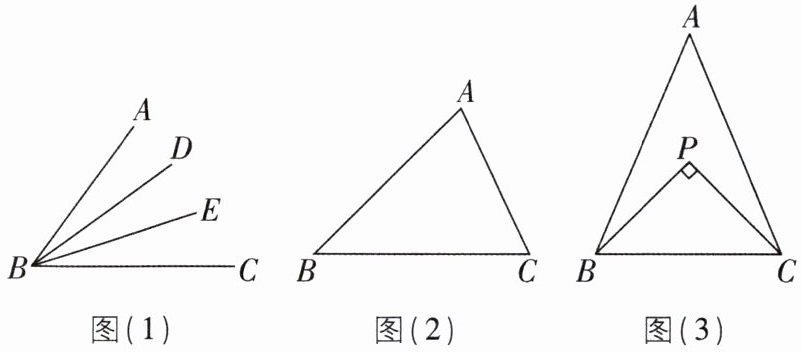
5 核心素养推理能力[难][概念认识]如图(1),在∠ABC中,若∠ABD = ∠DBE = ∠EBC,则BD,BE叫作∠ABC的“三分线”。其中,BD是“邻AB三分线”,BE是“邻BC三分线”。
[问题解决]
(1)如图(2),在△ABC中,∠A = 70°,∠B = 45°,若∠B的“三分线”BD交AC于点D,则∠BDC = ______；
(2)如图(3),在△ABC中,BP,CP分别是∠ABC的“邻AB三分线”和∠ACB的“邻AC三分线”,且BP ⊥ CP,求∠A的度数；
[延伸推广]
(3)在△ABC中,∠ACD是△ABC的外角,∠ABC的“三分线”所在的直线与∠ACD的“三分线”所在的直线交于点P。若∠A = m°,∠ABC = n°,请直接写出∠BPC的度数。(用含m,n的代数式表示)

[答案]：【解】(1)如图(1)，当 BD 是“邻 AB 三分线”时，∠ABD' = $\frac{1}{3}$×45° = 15°，∴∠BD'C = 70° + 15° = 85°；当 BD 是“邻 BC 三分线”时，∠ABD'' = $\frac{2}{3}$×45° = 30°，∴∠BD''C = 70° + 30° = 100°。故答案为 85°或 100°.(2)∵BP⊥CP，∴∠BPC = 90°，∴∠PBC + ∠PCB = 90°。又∵BP，CP 分别是∠ABC 的“邻 AB 三分线”和∠ACB 的“邻 AC 三分线”，∴∠PBC = $\frac{2}{3}$∠ABC，∠PCB = $\frac{2}{3}$∠ACB，∴$\frac{2}{3}$∠ABC + $\frac{2}{3}$∠ACB = 90°，∴∠ABC + ∠ACB = 135°。在△ABC 中，∠A + ∠ABC + ∠ACB = 180°，∴∠A = 180° - (∠ABC + ∠ACB) = 45°.(3)∠BPC 的度数为$\frac{2}{3}$m°或$\frac{1}{3}$m°或$\frac{2}{3}$m° + $\frac{1}{3}$n°或$\frac{1}{3}$m° - $\frac{1}{3}$n°或$\frac{1}{3}$n° - $\frac{1}{3}$m°。分四种情况进行画图计算：①如图(2)，当 BP 和 CP 分别是“邻 AB 三分线”“邻 AC 三分线”时，∠BPC = $\frac{2}{3}$∠A = $\frac{2}{3}$m°；②如图(3)，当 BP 和 CP 分别是“邻 BC 三分线”“邻 CD 三分线”时，∠BPC = $\frac{1}{3}$∠A = $\frac{1}{3}$m°；③如图(4)，当 BP 和 CP 分别是“邻 BC 三分线”“邻 AC 三分线”时，∠BPC = $\frac{2}{3}$∠A + $\frac{1}{3}$∠ABC = $\frac{2}{3}$m° + $\frac{1}{3}$n°；④如图(5)、图(6)，当 BP 和 CP 分别是“邻 AB 三分线”“邻 CD 三分线”时，当 m ＞ n 时，∠BPC = $\frac{1}{3}$∠A - $\frac{1}{3}$∠ABC = $\frac{1}{3}$m° - $\frac{1}{3}$n°；当 m ＜ n 时，∠BPC = $\frac{1}{3}$∠ABC - $\frac{1}{3}$∠A = $\frac{1}{3}$n° - $\frac{1}{3}$m°。综上所述，∠BPC 的度数为$\frac{2}{3}$m°或$\frac{1}{3}$m°或$\frac{2}{3}$m° + $\frac{1}{3}$n°或$\frac{1}{3}$m° - $\frac{1}{3}$n°或$\frac{1}{3}$n° - $\frac{1}{3}$m°.
5 核心素养推理能力[难][概念认识]如图(1),在∠ABC中,若∠ABD = ∠DBE = ∠EBC,则BD,BE叫作∠ABC的“三分线”。其中,BD是“邻AB三分线”,BE是“邻BC三分线”。
[问题解决]
(1)如图(2),在△ABC中,∠A = 70°,∠B = 45°,若∠B的“三分线”BD交AC于点D,则∠BDC = ______；
(2)如图(3),在△ABC中,BP,CP分别是∠ABC的“邻AB三分线”和∠ACB的“邻AC三分线”,且BP ⊥ CP,求∠A的度数；
[延伸推广]
(3)在△ABC中,∠ACD是△ABC的外角,∠ABC的“三分线”所在的直线与∠ACD的“三分线”所在的直线交于点P。若∠A = m°,∠ABC = n°,请直接写出∠BPC的度数。(用含m,n的代数式表示)

85°或100°45°$\frac{2}{3}$m°或$\frac{1}{3}$m°或$\frac{2}{3}$m° + $\frac{1}{3}$n°或$\frac{1}{3}$m° - $\frac{1}{3}$n°或$\frac{1}{3}$n° - $\frac{1}{3}$m°

答案： 【解】
(1)如图
(1)，当 BD 是“邻 AB 三分线”时，∠ABD' = $\frac{1}{3}$×45° = 15°，
∴∠BD'C = 70° + 15° = 85°；当 BD 是“邻 BC 三分线”时，∠ABD'' = $\frac{2}{3}$×45° = 30°，
∴∠BD''C = 70° + 30° = 100°。故答案为 85°或 100°.
(2)
∵BP⊥CP，
∴∠BPC = 90°，
∴∠PBC + ∠PCB = 90°。又
∵BP，CP 分别是∠ABC 的“邻 AB 三分线”和∠ACB 的“邻 AC 三分线”，
∴∠PBC = $\frac{2}{3}$∠ABC，∠PCB = $\frac{2}{3}$∠ACB，
∴$\frac{2}{3}$∠ABC + $\frac{2}{3}$∠ACB = 90°，
∴∠ABC + ∠ACB = 135°。在△ABC 中，∠A + ∠ABC + ∠ACB = 180°，
∴∠A = 180° - (∠ABC + ∠ACB) = 45°.
(3)∠BPC 的度数为$\frac{2}{3}$m°或$\frac{1}{3}$m°或$\frac{2}{3}$m° + $\frac{1}{3}$n°或$\frac{1}{3}$m° - $\frac{1}{3}$n°或$\frac{1}{3}$n° - $\frac{1}{3}$m°。分四种情况进行画图计算：①如图
(2)，当 BP 和 CP 分别是“邻 AB 三分线”“邻 AC 三分线”时，∠BPC = $\frac{2}{3}$∠A = $\frac{2}{3}$m°；②如图
(3)，当 BP 和 CP 分别是“邻 BC 三分线”“邻 CD 三分线”时，∠BPC = $\frac{1}{3}$∠A = $\frac{1}{3}$m°；③如图
(4)，当 BP 和 CP 分别是“邻 BC 三分线”“邻 AC 三分线”时，∠BPC = $\frac{2}{3}$∠A + $\frac{1}{3}$∠ABC = $\frac{2}{3}$m° + $\frac{1}{3}$n°；④如图
(5)、图
(6)，当 BP 和 CP 分别是“邻 AB 三分线”“邻 CD 三分线”时，当 m ＞ n 时，∠BPC = $\frac{1}{3}$∠A - $\frac{1}{3}$∠ABC = $\frac{1}{3}$m° - $\frac{1}{3}$n°；当 m ＜ n 时，∠BPC = $\frac{1}{3}$∠ABC - $\frac{1}{3}$∠A = $\frac{1}{3}$n° - $\frac{1}{3}$m°。综上所述，∠BPC 的度数为$\frac{2}{3}$m°或$\frac{1}{3}$m°或$\frac{2}{3}$m° + $\frac{1}{3}$n°或$\frac{1}{3}$m° - $\frac{1}{3}$n°或$\frac{1}{3}$n° - $\frac{1}{3}$m°.