《2025年初中必刷题八年级数学上册人教版》

1 满足下列条件的三条线段$a,b,c$能组成三角形的是 (C)
A.$a:b:c= 1:2:3$
B.$a+b= 4,a+b+c= 9$
C.$a= 3,b= 4,c= 5$
D.$a= 3t,b= 2t,c= t$

答案： C 【解析】根据三角形的三边关系可知，任意两边之和大于第三边，任意两边之差小于第三边。
A 设a,b,c分别为x,2x,3x,则有a+b=c,故不能组成三角形。
B 将a+b=4代入a+b+c=9,得c=5,4＜5,即a+b＜c,故不能组成三角形。
C 符合三角形的三边关系,故能组成三角形。
D a=b+c,故不能组成三角形。

2 [2024山西太原期中]王老师有长度分别为$a,b$的两根小棒(如图),如果要把其中的一根剪成两段,那么在下列选项的剪法中,三根小棒一定能围成三角形的是 (B)

A.将长为$a$的小棒正中间剪一刀
B.将长为$b$的小棒正中间剪一刀
C.将长为$a$的小棒任意剪一刀
D.将长为$b$的小棒任意剪一刀

答案： B 【解析】
∵b＞a,
∴由三角形三边关系得到将长为b的小棒正中间剪一刀，三根小棒一定能围成三角形。故选B。

3 [2025安徽马鞍山期中]三角形的三边长分别为$5,7,x$,则第三边长$x$的取值范围是2＜x＜12.

答案： 2＜x＜12 【解析】由题意得第三边长x的取值范围是7−5＜x＜7+5,即2＜x＜12,故答案为2＜x＜12。

4 [2025贵州遵义期中]若$a,b,c为\triangle ABC$的三边长,则$(a-b+c)(a-b-c)$＜$0$(填“$＞$”“$＜$”或“$=$”).

答案： ＜ 【解析】
∵a,b,c是△ABC的三边长,
∴a+c＞b,b+c＞a,
∴a−b+c＞0,a−b−c＜0,
∴(a−b+c)(a−b−c)＜0,故答案为＜。

5 [2025河北邢台期末]如图,在同一平面内有三个点$A,B,C$.

(1)利用尺规,按下面的要求作图(不写作法,保留作图痕迹).
①作射线$BA$;
②作线段$BC$;
③连接$AC$,并在线段$AC上截一条线段AD$,使$AD= AB$,连接$BD$.
(2)观察(1)得到的图形,$DB+DC$____$BC$(填“$＞$”“$＜$”或“$=$”).

答案：
【解】
(1)如图所示.①射线BA即为所求作.②线段BC即为所求作.③线段AC,AD,BD即为所求作。

(2)在△DBC中,DB+DC＞BC.故答案为＞。

6 [2025辽宁沈阳质检]如图,在$\triangle ABC$中,点$D在AB$上,点$O在CD$上.求证:$AB+AC＞OB+OC$.

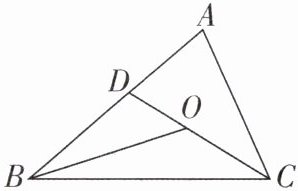
答案：
【证明】延长BO交AC于点E,如图。

在△EOC中,EO+EC＞OC,
∴EO+EC+OB＞OC+OB,即EB+EC＞OC+OB。在△ABE中,AB+AE＞EB,
∴AB+AE+EC＞EB+EC,即AB+AC＞EB+EC,
∴AB+AC＞OB+OC。

7 [2024贵州遵义期中]如图,工人师傅做了一个长方形窗框$ABCD$,$E,F,G,H$分别是四条边上的中点,为了使它更加稳固,需要在窗框上钉一根木条,这根木条不应钉在 (D)
A.$A,G$两点处
B.$G,H$两点处
C.$B,F$两点处
D.$E,G$两点处

答案： D 【解析】由题意可知，为了窗框稳固，需要在窗框上钉一根木条，根据三角形具有稳定性，这根木条钉在E,G两点处时,不能构成三角形，所以不应该钉在E,G两点处。故选D。

8 [2025吉林松原期中]如图,自行车框架中的$AB$,$AC$,$BC$构成一个几何图形,其可使得自行车结构更加稳固,这里所运用的几何原理是三角形具有稳定性.

答案： 三角形具有稳定性 【解析】因为AB,AC,BC构成的几何图形是三角形，所以使自行车结构更加稳固用到的几何原理是三角形具有稳定性。故答案为三角形具有稳定性。

9 若等腰三角形两边长分别为$4,9$,则其周长为22.

答案： 22 【解析】①若4是腰长，则底边长是9,但是4+4＜9,故不能构成三角形，舍去。②若4是底边长，则腰长是9,4+9＞9，符合三角形三边关系，成立。故等腰三角形的周长为4+9+9=22。