《2025年初中必刷题八年级数学上册人教版》

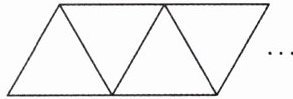
1 [2025 云南玉溪期末]用小木棒按如图的方式搭一行等边三角形,搭 1 个三角形需 3 根小木棒,搭 2 个三角形需 5 根小木棒,搭 3 个三角形需 7 根小木棒,…,照这样的规律搭下去,搭 2024 个三角形需要小木棒的根数为 (C)

A.4048
B.6060
C.4049
D.6042

答案： C【解析】由题图可知，搭1个三角形所需小木棒的根数为3=1×2+1；搭2个三角形所需小木棒的根数为5=2×2+1；搭3个三角形所需小木棒的根数为7=3×2+1；搭4个三角形所需小木棒的根数为9=4×2+1；…，所以搭n个三角形所需小木棒的根数为2n+1，当n=2024时，2n+1=2×2024+1=4049，即搭2024个三角形所需小木棒的根数为4049.

用材质、规格均相同的 24 根火柴棒搭一个三角形(全部用完),则一共可搭12种形状不同的三角形,其中等边三角形有1个.

答案： 12 1【解析】设每根火柴棒的长度均为1.
∵三角形两边之和大于第三边，两边之差小于第三边，三边共用24根火柴棒，
∴三角形三边长度如下：①2,11,11；②3,10,11；③4,9,11；④4,10,10；⑤5,8,11；⑥5,9,10；⑦6,7,11；⑧6,8,10；⑨6,9,9；⑩7,7,10；⑪7,8,9；⑫8,8,8.综上，一共可搭12种形状不同的三角形，其中等边三角形有1个.故答案为12,1.

3 在平面内,分别用相同的 3 根,5 根,6 根,…火柴首尾顺次相接,能搭成什么形状的三角形呢? 通过尝试,列表如下: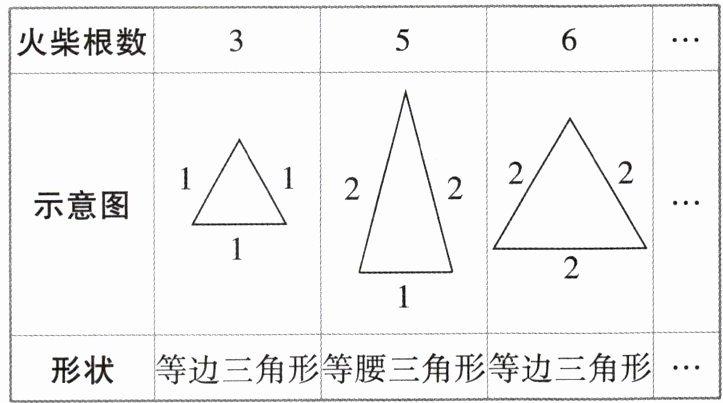
根据以上信息,解答下列问题:
(1)4 根火柴能搭成三角形吗?
(2)12 根火柴能搭成几种不同形状的三角形? 请画出它们的示意图.(提示:如果三角形的三边长 a,b,c 满足 $ a^{2}+b^{2}= c^{2} $,那么这个三角形是直角三角形)

答案：
【解】
(1)4根火柴不能搭成三角形.
(2)12根火柴能搭成3种不同形状的三角形.示意图如下:
　　　 　　 　　
　　　等边三角形　等腰三角形　直角三角形

4 [2025 广东河源期末]

如

图

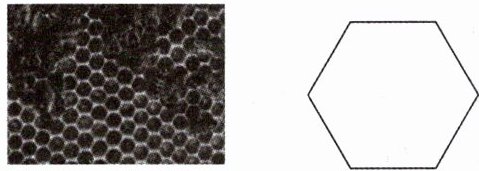
所示的蜂巢由许多六边形构成,将六边形三角剖分,可以分割成三角形的个数为 ( )


A.6
B.5
C.4
D.3

答案：
C【解析】如图，连接对角线，可知一个六边形可以分割成4个三角形.故选C.
　　　　　　　

5 [2025 河南周口质检]五边形可以通过三角剖分分割出 3 个三角形,则共有几种剖分方法 (D)
A.2
B.3
C.4
D.5

答案： D【解析】从五边形的一个顶点出发，可以连接两条对角线，得到3个三角形.
∵五边形有5个顶点，
∴共有5种剖分方法.

6 [2025 江苏苏州质检]从一个多边形的同一个顶点出发,分别连接这个顶点与其余各顶点,可以把这个多边形分割成若干个三角形. 根据下面的图形反映出来的规律,n 边形从一个顶点出发被分割成的三角形的个数为n-2.

答案： n-2【解析】由题图可以看出，四边形被分为4-2=2(个)三角形，五边形被分为5-2=3(个)三角形，六边形被分为6-2=4(个)三角形，…，那么n边形可以被分为(n-2)个三角形.

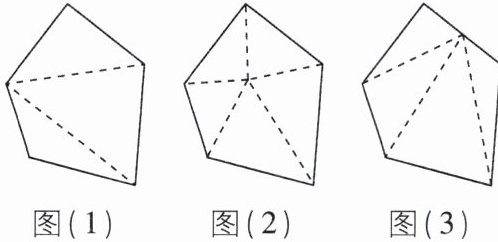
7 [2025 山西太原期中]如图,用三种方法分割五边形.
(1)三种分割方法把多边形分成的三角形的个数与多边形的边数有没有关系? 若有关系,具体是什么关系?
(2)若是 n(n 为大于 3 的整数)边形,请分别写出用上述三种方法分割所得三角形的个数.

答案： 【解】
(1)有关系.关系如下：题图
(1)中，三角形的个数=多边形的边数-2；题图
(2)中，三角形的个数=多边形的边数；题图
(3)中，三角形的个数=多边形的边数-1.
(2)由
(1)得，若是n(n为大于3的整数)边形，三种方法分割所得三角形的个数依次为n-2,n,n-1.