《2025年初中必刷题八年级数学上册人教版》

1 [中]如图(1)所示,将长为6的长方形纸片沿虚线折成3个小长方形,其中左右两侧长方形的宽相等,若要将其围成如图(2)所示的三棱柱形物体,则图中$a$的值可以是 (B)
A.1
B.2
C.3
D.4

答案： B 【解析】因为长为6的线段围成的等腰三角形的腰长为a,所以底边长为6−2a。由三角形的三边关系可得{2a＞6 - 2a,6 - 2a＞0}，解得$\frac{3}{2}$＜a＜3。所以a的值可以是2,故选B。

已知关于$x$的不等式组$\begin{cases}x-a＜0,\\2x-1\geqslant7\end{cases} $至少有两个整数解,且存在三边长为$3,a,7$的三角形,则$a$的整数解有 (C)
A.2个
B.3个
C.4个
D.5个

答案： C 【解析】解不等式x−a＜0,可得x＜a；解不等式2x−1≥7,可得x≥4。因为不等式组至少有两个整数解，所以一定包含4和5。
画数轴：−1 0 1 2 3 4 5 a 6
定范围：因为表示a的点上画的是空心圆圈，所以不能取到5，所以a＞5。因为存在三边长为3,a,7的三角形，所以4＜a＜10,故5＜a＜10,所以a的整数解有4个,故选C。
易错警示：对于等腰三角形不能确定哪条边是腰或底边时，要分情况讨论，还要注意判断分情况后的三条线段能否构成三角形。
思路分析：
(1)利用三角形任意两边之和大于第三边，任意两边之差小于第三边建立不等式组即可解决问题。

3 [2025河北邯郸质检,中]如图,一根直的铁丝$AB= 20\mathrm{cm}$,欲将其弯折成一个三角形,在同一平面内操作如下:

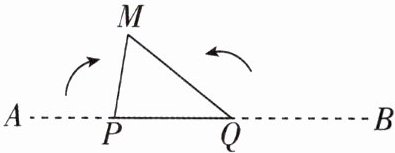
①量出$AP= 5\mathrm{cm}$;
②在点$P右侧取一点Q$,使$PQ＞5\mathrm{cm}$;
③将$AP$向右翻折,$BQ$向左翻折.
若要使$A,B两点能在点M$处重合,则$PQ$的长度可能是 (D)
A.$12\mathrm{cm}$
B.$11\mathrm{cm}$
C.$10\mathrm{cm}$
D.$7\mathrm{cm}$

答案： D 【解析】设PQ=x cm(x＞5)。
∵AP=5 cm,PQ=x cm,
∴BQ=AB−AP−PQ=20−5−x=(15−x)cm。由AP向右翻折,BQ向左翻折,可知AP=MP,MQ=BQ。
∵△MPQ符合三角形三边关系,
∴MQ−MP＜PQ＜MQ+MP,即15−x−5＜x＜15−x+5,解得5＜x＜10,故选D。

4 [2024北京海淀区调研,中]若三角形的三边长是三个连续自然数,其周长$m满足1986＜m＜2022$,则这样的三角形有11个.

答案： 11 【解析】设中间的数为x,则前面一个数为x−1,后面一个数为x+1。由题意得{986＜x - 1+x+x + 1＜2022,x - 1+x＞x + 1}，解得662＜x＜674。
∵x为自然数,
∴x=663,664,665,…,673,
∴这样的三角形有11个。故答案为11。

现有长为$60\mathrm{cm}$的铁丝,要截成$n(n＞2)$段,每段的长为不小于$1\mathrm{cm}$的整数,如果其中任意3段都不能拼成三角形,当$n$取最大值时,有6种方法将该铁丝截成满足条件的$n$段.

答案： 6 【解析】
∵n段之和为定值60 cm,
∴要让n尽可能大,必须每段长度尽可能小,而每段长度为不小于1 cm的整数,且任意3段不能拼成三角形,
∴任意3段中最长的一段的长度不小于其他2段长度之和,因此这些截成的小段的长度(单位:cm)只可能是1,1,2,3,5,8,13,21,34,55。
∵1+1+2+3+5+8+13+21=54＜60,1+1+2+3+5+8+13+21+34=88＞60,
∴n的最大值是8。将长为60 cm的铁丝截成满足条件的8段,共有下列6种方式:①1,1,2,3,5,8,13,27;②1,1,2,3,5,8,14,26;③1,1,2,3,5,8,15,25;④1,1,2,3,5,8,16,24;⑤1,1,2,3,5,9,14,25;⑥1,1,2,3,5,9,15,24。故答案为6。

6 [2025湖北武汉质检,中]已知$\triangle ABC的三边长a,b,c满足a+b= 3c-4,a-b= 2c-6$,且$a＞b$.
(1)求$c$的取值范围;
(2)若$\triangle ABC$的周长为12,求$c$的值.

答案： 【解】
(1)由题意得a−b＜c＜a+b,且a+b=3c−4,a−b=2c−6,
∴2c−6＜c＜3c−4,
∴2＜c＜6。又
∵a＞b,
∴a−b=2c−6＞0,
∴c＞3,
∴3＜c＜6。
(2)
∵△ABC的周长为12,
∴a+b+c=12。又
∵a+b=3c−4,
∴3c−4+c=12,
∴c=4。

(1)以下4组长度的小木棍能组成“不均衡三角形”的为②(填序号).
(2)已知“不均衡三角形”三边长分别为$2x+2,16,2x-6$($x$为整数),求$x$的值.
【解】(2)因为2x+2＞2x−6,所以需分三种情况:
①16＞2x+2＞2x−6,解得x＜7,此时有16−(2x+2)＞2x+2−(2x−6),解得x＜3。因为2x−6＞0,解得x＞3,所以不合题意，舍去;
②2x+2＞16＞2x−6,解得7＜x＜11,此时有2x+2−16＞16−(2x−6),解得x＞9,故9＜x＜11。因为x为整数,所以x=10。当x=10时,2x+2=2×10+2=22,2x−6=2×10−6=14,易知长为22,16,14的线段可组成三角形。
③2x+2＞2x−6＞16,解得x＞11,此时有2x+2−(2x−6)＞2x−6−16,解得x＜15,故11＜x＜15。因为x为整数,所以x=12或13或14。易知当x=12或13或14时,可以组成三角形。
综上所述,x的整数值为10或12或13或14。

答案： 【解】
(1)①中,1+2＜4,故长为4 cm,2 cm,1 cm的小木棍不能组成“不均衡三角形”;②中,18−13＞13−9,所以长为13 cm,18 cm,9 cm的小木棍能组成“不均衡三角形”;③中,19=19,所以长为19 cm,20 cm,19 cm的小木棍不能组成“不均衡三角形”;④中,9−8＜8−6,所以长为9 cm,8 cm,6 cm的小木棍不能组成“不均衡三角形”。故答案为②。
(2)因为2x+2＞2x−6,所以需分三种情况:
①16＞2x+2＞2x−6,解得x＜7,此时有16−(2x+2)＞2x+2−(2x−6),解得x＜3。因为2x−6＞0,解得x＞3,所以不合题意，舍去;
②2x+2＞16＞2x−6,解得7＜x＜11,此时有2x+2−16＞16−(2x−6),解得x＞9,故9＜x＜11。因为x为整数,所以x=10。当x=10时,2x+2=2×10+2=22,2x−6=2×10−6=14,易知长为22,16,14的线段可组成三角形。
③2x+2＞2x−6＞16,解得x＞11,此时有2x+2−(2x−6)＞2x−6−16,解得x＜15,故11＜x＜15。因为x为整数,所以x=12或13或14。易知当x=12或13或14时,可以组成三角形。
综上所述,x的整数值为10或12或13或14。
关键点拨：判断是否组成三角形的步骤：
(1)由于边长中含有参数，需要分类讨论。
(2)因为2x+2一定大于2x−6,所以只需按边长为16的边在三角形三边中的大小关系分三种情况讨论。
(3)三边的长度确定后,均需要用三角形三边关系检验是否能组成三角形。