《2025年初中必刷题八年级数学上册人教版》

1 [2025 山东临沂期末,中]如图是一台起重机的工作简图,前后两次吊杆位置 $OP_1$, $OP_2$ 与线绳(线绳垂直于地面)的夹角分别是 $35^{\circ}$ 和 $80^{\circ}$,则吊杆前后两次的夹角 $\angle P_1OP_2$ 的度数为 ( )

A.$55^{\circ}$
B.$45^{\circ}$
C.$40^{\circ}$
D.$35^{\circ}$

答案：
B 【解析】如图，由题意知$P_{1}B$，$P_{2}A$垂直于 OA.在$\text{Rt}\triangle OAP_{2}$中，$∠AOP_{2}=90^{\circ }-80^{\circ }=10^{\circ }$，在$\text{Rt}\triangle OBP_{1}$中，$∠BOP_{1}=90^{\circ }-35^{\circ }=55^{\circ }$，$\therefore$$∠P_{1}OP_{2}=∠P_{1}OA-∠P_{2}OA=55^{\circ }-10^{\circ }=45^{\circ }$.故选 B.

2 [中]如图,在由 25 个边长为 1 的小正方形拼成的网格中,以 $AB$ 为边画 $Rt\triangle ABC$,使点 $C$ 在格点上,满足这样条件的点 $C$ 共有 ( )

A.5 个
B.6 个
C.7 个
D.8 个

答案：
D 【解析】根据题意可得以 AB 为边画$\text{Rt}\triangle ABC$，使点 C 在格点上，满足这样条件的点 C 共 8 个，如图所示.故选 D.

3 [中]已知非直角三角形 $ABC$ 中, $\angle A = 45^{\circ}$,高 $BD$ 与高 $CE$ 所在直线交于点 $H$, 则 $\angle BHC$ 的度数是______.

答案：
$135^{\circ }$或$45^{\circ }$【解析】①如图（1），$\triangle ABC$是锐角三角形时，$\because$BD，CE 是$\triangle ABC$的高线，$\therefore$$∠ADB=90^{\circ }$，$∠BEC=90^{\circ }$.在$\triangle ABD$中，$\because$$∠A=45^{\circ }$，$\therefore$$∠ABD=90^{\circ }-45^{\circ }=45^{\circ }$.在$\text{Rt}\triangle BEH$中，$∠EHB=90^{\circ }-45^{\circ }=45^{\circ }$，$\therefore$$∠BHC=180^{\circ }-∠EHB=180^{\circ }-45^{\circ }=135^{\circ }$.

②如图（2），$\triangle ABC$是钝角三角形时，$\because$BD，CE 是$\triangle ABC$的高线，$\therefore$$∠A+∠ACE=90^{\circ }$，$∠BHC+∠HCD=90^{\circ }$.$\because$$∠ACE=∠HCD$（对顶角相等），$\therefore$$∠BHC=∠A=45^{\circ }$.综上所述，$∠BHC$的度数是$135^{\circ }$或$45^{\circ }$.

4 [2024 江苏盐城校级质检,中]在 $\triangle ABC$ 中, $AB = AC$,将 $\triangle ABC$ 折叠,使 $A$, $B$ 两点重合,折痕所在直线与 $AC$ 边所在直线的夹角为 $40^{\circ}$,则 $\angle A$ 的度数为______.

答案：
$50^{\circ }$或$130^{\circ }$【解析】分两种情况讨论：①如图（1），由折叠的性质可知$EF⊥AB$，$\therefore$$∠AEF=90^{\circ }$.$\because$折痕所在直线与 AC 边所在直线的夹角为$40^{\circ }$，$\therefore$$∠AFE=40^{\circ }$，$\therefore$$∠A=90^{\circ }-40^{\circ }=50^{\circ }$.

②如图（2），由折叠的性质可知$EF⊥AB$，$\therefore$$∠AFD=90^{\circ }$.$\because$折痕所在直线与 AC 边所在直线的夹角为$40^{\circ }$，$\therefore$$∠D=40^{\circ }$，$\therefore$$∠DAB=90^{\circ }-∠D=90^{\circ }-40^{\circ }=50^{\circ }$，$\therefore$$∠BAC=180^{\circ }-∠DAB=180^{\circ }-50^{\circ }=130^{\circ }$.故答案为$50^{\circ }$或$130^{\circ }$.

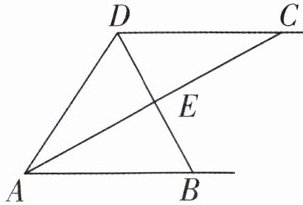
5 [2025 浙江杭州质检,中]如图, $AB // CD$, $AC$ 平分 $\angle BAD$, $BD$ 平分 $\angle ADC$, $AC$ 和 $BD$ 交于点 $E$. 写出图中所有的直角三角形.

答案： 【解】$\because$$AB// CD$，$\therefore$$∠ADC+∠BAD=180^{\circ }$.
思路分析
分$\triangle ABC$是锐角三角形与钝角三角形两种情况讨论，结合直角三角形的性质求解即可.
关键点拨
本题主要考查的是折叠的性质和直角三角形的性质，根据题意画出图形是解题的关键.
$\because$AC 平分$∠BAD$，BD 平分$∠ADC$，$\therefore$$∠DAE=\frac {1}{2}∠BAD$，$∠ADE=\frac {1}{2}∠ADC$，$\therefore$$∠ADE+∠DAE=\frac {1}{2}∠ADC+\frac {1}{2}∠BAD=\frac {1}{2}(∠ADC+∠BAD)=90^{\circ }$，$\therefore$$∠AED=90^{\circ }$.$\because$AC 和 BD 交于点 E，$\therefore$$∠DEC=∠AEB=∠AED=90^{\circ }$，$\therefore$$\triangle AED$，$\triangle AEB$，$\triangle DEC$均为直角三角形.

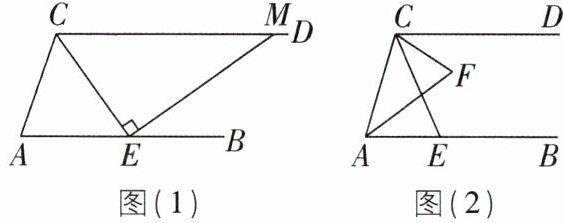
6 核心素养 几何直观 [2024 重庆沙坪坝区期末,较难]如图, $AB // CD$,点 $E$ 是 $AB$ 上一点,连接 $CE$.
(1)如图(1),若 $CE$ 平分 $\angle ACD$,过点 $E$ 作 $EM \perp CE$ 交 $CD$ 于点 $M$,试说明 $\angle A = 2\angle CME$;
(2)如图(2),若 $AF$ 平分 $\angle CAB$, $CF$ 平分 $\angle DCE$,且 $\angle F = 70^{\circ}$,求 $\angle ACE$ 的度数;
(3)如图(3),过点 $E$ 作 $EM \perp CE$ 交 $\angle DCE$ 的平分线于点 $M$, $MN \perp CM$ 交 $AB$ 于点 $N$, $CH \perp AB$,垂足为 $H$. 若 $\angle ACH = \frac{1}{2}\angle ECH$,请直接写出 $\angle MNB$ 与 $\angle A$ 之间的数量关系.

答案：
【解】（1）$\because$$EM⊥CE$，$\therefore$$∠CEM=90^{\circ }$，$\therefore$$∠ECD+∠CME=90^{\circ }$，$\therefore$$2∠ECD+2∠CME=180^{\circ }$.$\because$CE 平分$∠ACD$，$\therefore$$∠ACD=2∠ECD$，$\therefore$$∠ACD+2∠CME=180^{\circ }$.$\because$$AB// CD$，$\therefore$$∠ACD+∠A=180^{\circ }$，$\therefore$$∠A=2∠CME$.
（2）如图（1），过点 F 作$FM// AB$.
$\because$$AB// CD$，$\therefore$$FM// AB// CD$，$\therefore$$∠AFM=∠BAF$，$∠CFM=∠DCF$，$\therefore$$∠AFM+∠CFM=∠BAF+∠DCF$，即$∠AFC=∠BAF+∠DCF$.$\because$AF 平分$∠CAB$，CF 平分$∠DCE$，$\therefore$$∠CAB=2∠BAF$，$∠DCE=2∠DCF$，$\therefore$$∠CAB+∠DCE=2(∠BAF+∠DCF)=2∠AFC$.$\because$$∠AFC=70^{\circ }$，$\therefore$$∠CAB+∠DCE=140^{\circ }$.$\because$$AB// CD$，$\therefore$$∠CAB+∠ACD=∠CAB+∠ACE+∠DCE=180^{\circ }$，$\therefore$$∠ACE=180^{\circ }-(∠CAB+∠DCE)=180^{\circ }-140^{\circ }=40^{\circ }$.

（3）$∠MNB$与$∠A$之间的数量关系是$∠MNB=135^{\circ }-∠A$.如图（2），延长 CM 交 AB 于点 G.$\because$$MN⊥CM$，$\therefore$$∠NMG=90^{\circ }$，$\therefore$$∠MNB=90^{\circ }-∠MGN$，同理$∠HCG=90^{\circ }-∠MGN$，$\therefore$$∠MNB=∠HCG$.$\because$$∠ACH=\frac {1}{2}∠ECH$，$\therefore$设$∠ACH=x$，则$∠ECH=2x$.$\because$CM 平分$∠DCE$，$\therefore$设$∠ECM=∠DCM=y$，$\therefore$$∠MNB=∠HCG=2x+y$.$\because$$AB// CD$，$CH⊥AB$，$\therefore$$CH⊥CD$，$\therefore$$∠HCD=90^{\circ }$，$\therefore$$∠ECH+∠ECD=90^{\circ }$，$\therefore$$2x+2y=90^{\circ }$，$\therefore$$x+y=45^{\circ }$.$\because$$CH⊥AB$，$\therefore$$∠A=90^{\circ }-∠ACH=90^{\circ }-x$，$\therefore$$∠A+∠MNB=90^{\circ }-x+2x+y=90^{\circ }+x+y=135^{\circ }$，$\therefore$$∠MNB=135^{\circ }-∠A$.