《2025年初中必刷题八年级数学上册人教版》

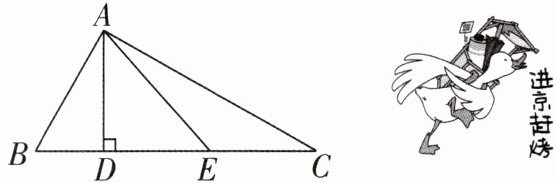
1[2024陕西中考]如图,在△ABC中,∠BAC= 90°,AD是BC边上的高,E是DC的中点,连接AE,则图中的直角三角形共有(C)

A.2个
B.3个
C.4个
D.5个

答案： 1. C 【解析】由题意得△ABD，△ABC，△ADC，△ADE均为直角三角形，
∴共有4个直角三角形.故选C.

用一根小木棒与两根长度分别为3cm,5cm的小木棒组成三角形,则这根小木棒的长度可以是(B)
A.9cm
B.7cm
C.2cm
D.1cm

答案： 2. B 【解析】设这根小木棒长为x cm.由三角形三边关系得5 - 3 ＜ x ＜ 5 + 3，所以x的取值范围是2 ＜ x ＜ 8，观察选项，只有选项B符合题意.故选B.

若长度分别为3,6,a的三条线段能组成一个三角形,则整数a的值可以是4.(写出一个即可)

答案： 3. 4(答案不唯一) 【解析】
∵长度分别为3,6,a的三条线段能组成一个三角形，
∴6 - 3 ＜ a ＜ 6 + 3，
∴3 ＜ a ＜ 9，
∴整数a的值可以是4，故答案为4(答案不唯一).

如图,在△ABC中,AD是高,AE是中线,AD= 4,$S_{△ABC}= 12,$则BE的长为(B)
A.1.5
B.3
C.4
D.6

答案： 4. B 【解析】
∵S△ABC = $\frac{1}{2}$BC×AD = 12，AD = 4，
∴BC = 6.
∵AE是中线，
∴BE = $\frac{1}{2}$BC = 3，故选B.

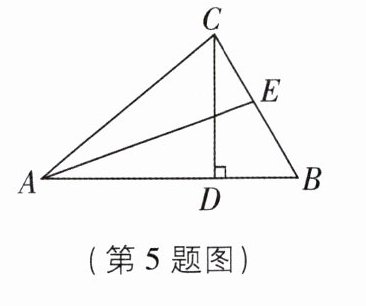
5[2024四川凉山州中考]如图,△ABC中,∠BCD= 30°,∠ACB= 80°,CD是边AB上的高,AE是∠CAB的平分线,则∠AEB的度数是______.

100°

答案： 5. 100° 【解析】
∵∠BCD = 30°，∠ACB = 80°，
∴∠ACD = 50°.
∵CD是边AB上的高，
∴∠ADC = 90°，
∴∠DAC = 40°.
∵AE是∠CAB的平分线，
∴∠CAE = $\frac{1}{2}$∠DAC = 20°，
∴∠AEB = ∠CAE + ∠ACB = 20° + 80° = 100°.故答案为100°.

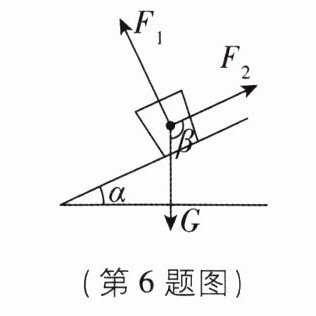
6新考向跨学科综合[2024山西中考]一只杯子静止在斜面上,其受力分析如图所示,重力G的方向竖直向下,支持力$F_1$的方向与斜面垂直,摩擦力$F_2$的方向与斜面平行.若斜面的坡角α= 25°,则摩擦力$F_2$与重力G方向的夹角β的度数为( )

A.155°
B.125°
C.115°
D.65°

答案：
6. C 【解析】如图，
∵重力G的方向竖直向下，
∴重力G与水平方向夹角为90°.
∵摩擦力F₂的方向与斜面平行，α = 25°，
∴β = ∠1 = α + 90° = 25° + 90° = 115°，故选C.

若三角形三个内角的比为1:2:3,则这个三角形是直角三角形.

答案： 7. 直角 【解析】设这个三角形最小的内角度数是x°，则另外两内角的度数分别为2x°，3x°.根据题意得x + 2x + 3x = 180，解得x = 30，
∴3x° = 3×30° = 90°，
∴这个三角形是直角三角形，故答案为直角.

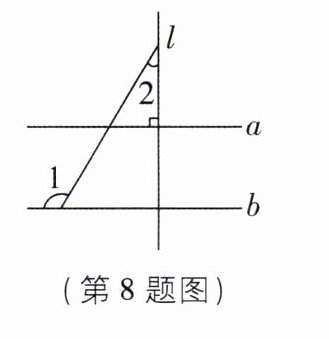
8[2024江苏连云港中考]如图,直线a//b,直线l⊥a,∠1= 120°,则∠2= ______°.

答案：
8. 30 【解析】如图.
∵a//b，
∴∠3 = ∠1 = 120°.
∵l⊥a，
∴∠3 = ∠2 + 90°，
∴∠2 = 30°.故答案为30.

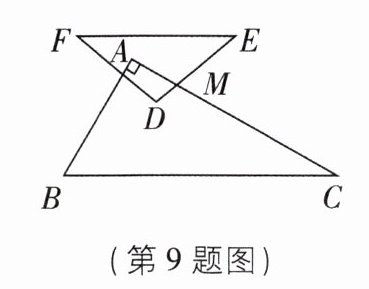
9[四川绵阳中考]两个三角形如图摆放,其中∠BAC= 90°,∠EDF= 100°,∠B= 60°,∠F= 40°,DE与AC交于点M,若BC//EF,则∠DMC的大小为______.

答案：
9. 110° 【解析】如图，延长ED交BC于点G.
∵∠BAC = 90°，∠B = 60°，
∴∠C = 90° - 60° = 30°.
∵∠EDF = 100°，∠F = 40°，
∴∠E = 180° - 40° - 100° = 40°.
∵BC//EF，
∴∠EGC = ∠E = 40°，
∴∠DMC = 180° - ∠EGC - ∠C = 110°.故答案为110°.

10[2023辽宁辽阳中考]如图,在三角形纸片ABC中,AB= AC,∠B= 20°,点D是边BC上的动点,将三角形纸片沿AD对折,使点B落在点B'处,当B'D⊥BC时,∠BAD的度数为______.

答案：
10. 25°或115° 【解析】由折叠的性质得∠ADB' = ∠ADB.
∵B'D⊥BC，
∴∠BDB' = 90°.分两种情况讨论:①当B'在BC下方时，如图
(1).
∵∠ADB + ∠ADB' + ∠BDB' = 360°，
∴∠ADB = $\frac{1}{2}$×(360° - 90°) = 135°，
∴∠BAD = 180° - ∠B - ∠ADB = 25°.
思路分析
分两种情况:①点B'在BC的下方，由折叠的性质及∠BDB' = 90°可知∠ADB' = ∠ADB = 135°，即可求得∠BAD = 25°;②点B'在BC的上方，由折叠的性质及∠BDB' = 90°可知∠ADB' = ∠ADB = 45°，即可求得∠BAD = 115°.
归纳总结
见平行，延长线段构造同位角、内错角或同旁内角.

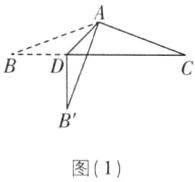
②当B'在BC上方时，如图
(2).
∵∠ADB + ∠ADB' = 90°，
∴∠ADB = $\frac{1}{2}$×90° = 45°，
∴∠BAD = 180° - ∠B - ∠ADB = 115°.综上，∠BAD的度数为25°或115°.故答案为25°或115°.