第57页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
汉字是中华文明的标志,它经历了甲骨文、金文、篆书、隶书、草书、楷书、行书的演变过程,每种书体都有着鲜明的艺术特征.下面文字属于轴对称图形的是(
C
)
答案:
1. C 【解析】只有 C 选项中的文字能找到这样的一条直线,使其沿这条直线折叠,直线两旁的部分能够互相重合,所以 C 选项中的文字是轴对称图形。
2 [2025 湖南长沙质检]已知网格中每个小正方形的边长都是 1,图(1)中的阴影图案是由四个小正方形组成的大正方形的一条对角线和以其中一个小正方形顶点为圆心、2 为半径所画的圆弧围成的弓形.请你在图(2)中以图(1)为基本图案,借助轴对称和平移设计一个图案,使该图案为轴对称图形.
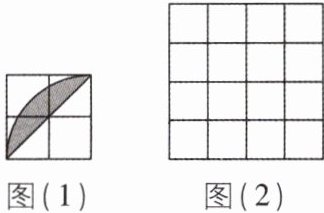

答案:
2.【解】如图所示(答案不唯一)。

2.【解】如图所示(答案不唯一)。

3 [2025 山西吕梁期中]问题情境:
数学活动课上,老师提出了一个问题:等腰三角形底边中点到两腰的距离相等吗?同学们就这个问题展开探究.
问题初探:
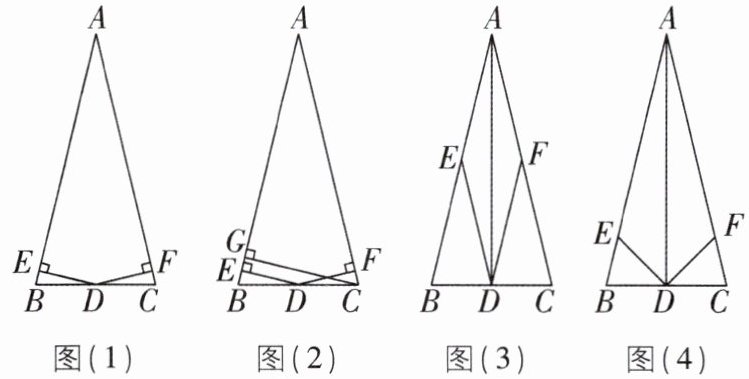
(1)希望小组的同学们根据题意画出了相应的图形,如图(1),在△ABC 中,AB = AC,D 是 BC 的中点,DE⊥AB,DF⊥AC,垂足分别为点 E,F.经过探究讨论,该小组的同学们得出的结论是 DE = DF,他们的证法如下:
证明:∵ DE⊥AB,DF⊥AC,∴ ∠DEB = ∠DFC = 90°.∵ AB = AC,∴ ∠B = ∠C(依据 1).∵ D 是 BC 的中点,∴ BD = CD.在△BDE 和△CDF 中,
$\left\{ \begin{array} { l } { ∠ D E B = ∠ D F C, } \\ { ∠ B = ∠ C, } \\ { B D = C D, } \end{array} \right.$
∴ △BDE ≌ △CDF(依据 2),∴ DE = DF.
①请写出依据 1 和依据 2 的内容:
依据 1:______.
依据 2:______.
②请你写出另一种证法.
问题再探:
(2)未来小组的同学们经过探究又有新的发现,如图(2),在△ABC 中,D 是 BC 的中点,DE⊥AB,DF⊥AC,垂足分别为 E,F,作腰 AB 上的高 CG,则 CG 与 DE 有确定的数量关系.请你直接写出这个数量关系:______.
类比探究:
(3)奋斗小组的同学们认真研究过后,发现了以下两个正确结论:①如图(3),在△ABC 中,AB = AC,D 为 BC 的中点,若 DE,DF 分别为△ABD 和△ACD 的中线,那么 DE = DF 仍然成立;②如图(4),在△ABC 中,AB = AC,D 为 BC 的中点,若 DE,DF 分别为△ABD 和△ACD 的角平分线,那么 DE = DF 仍然成立.请你选择其中一个结论证明.
数学活动课上,老师提出了一个问题:等腰三角形底边中点到两腰的距离相等吗?同学们就这个问题展开探究.
问题初探:
(1)希望小组的同学们根据题意画出了相应的图形,如图(1),在△ABC 中,AB = AC,D 是 BC 的中点,DE⊥AB,DF⊥AC,垂足分别为点 E,F.经过探究讨论,该小组的同学们得出的结论是 DE = DF,他们的证法如下:
证明:∵ DE⊥AB,DF⊥AC,∴ ∠DEB = ∠DFC = 90°.∵ AB = AC,∴ ∠B = ∠C(依据 1).∵ D 是 BC 的中点,∴ BD = CD.在△BDE 和△CDF 中,
$\left\{ \begin{array} { l } { ∠ D E B = ∠ D F C, } \\ { ∠ B = ∠ C, } \\ { B D = C D, } \end{array} \right.$
∴ △BDE ≌ △CDF(依据 2),∴ DE = DF.
①请写出依据 1 和依据 2 的内容:
依据 1:______.
依据 2:______.
②请你写出另一种证法.
问题再探:
(2)未来小组的同学们经过探究又有新的发现,如图(2),在△ABC 中,D 是 BC 的中点,DE⊥AB,DF⊥AC,垂足分别为 E,F,作腰 AB 上的高 CG,则 CG 与 DE 有确定的数量关系.请你直接写出这个数量关系:______.
类比探究:
(3)奋斗小组的同学们认真研究过后,发现了以下两个正确结论:①如图(3),在△ABC 中,AB = AC,D 为 BC 的中点,若 DE,DF 分别为△ABD 和△ACD 的中线,那么 DE = DF 仍然成立;②如图(4),在△ABC 中,AB = AC,D 为 BC 的中点,若 DE,DF 分别为△ABD 和△ACD 的角平分线,那么 DE = DF 仍然成立.请你选择其中一个结论证明.

答案:
3.
(1)【解】①依据1:等腰三角形的两个底角相等(或等边对等角)。依据2:两角分别相等且其中一组等角的对边相等的两个三角形全等(或角角边或 AAS)。故答案为等腰三角形的两个底角相等(或等边对等角),两角分别相等且其中一组等角的对边相等的两个三角形全等(或角角边或 AAS)。
关键点拔:利用等量代换及等式的性质得出∠CBF= 是解题关键。
思路分析:
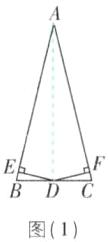
②另一种证法如下:如图
(1),连接 AD。
∵AB = AC,D 是 BC 的中点,
∴AD 是∠BAC 的平分线。
∵DE⊥AB,DF⊥AC,
∴DE = DF。(证法不唯一)
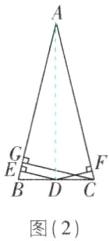
(2)【解】如图
(2),连接 AD。
∵AB = AC,D 是 BC 的中点,
∴AD 是∠BAC 的平分线。
∵DE⊥AB,DF⊥AC,
∴DE = DF。
∵S△ABC = S△ABD + S△ACD,
∴$\frac{1}{2}$×AB×CG = $\frac{1}{2}$×AB×DE + $\frac{1}{2}$×AC×DF,
∴CG = 2DE,故答案为 CG = 2DE。
(3)【证明】(任选一个证明即可)选择①:
∵DE,DF 分别是△ABD 和△ACD 的中线,
∴BE = $\frac{1}{2}$AB,CF = $\frac{1}{2}$AC。
∵AB = AC,
∴BE = CF,∠B = ∠C。又
∵D 是 BC 的中点,
∴BD = CD。在△BDE 与△CDF 中,$\begin{cases}BE = CF\\∠B = ∠C\\BD = CD\end{cases}$,
∴△BDE≌△CDF(SAS),
∴DE = DF。
选择②:
∵AB = AC,D 是 BC 的中点,
∴∠B = ∠C,BD = CD,AD⊥BC,
∴∠ADB = ∠ADC = 90°。又
∵DE,DF 分别是△ABD 和△ACD 的角平分线,
∴∠BDE = ∠CDF = 45°。在△BDE 与△CDF 中,$\begin{cases}∠B = ∠C\\BD = CD\\∠BDE = ∠CDF\end{cases}$,
∴△BDE≌△CDF(ASA),
∴DE = DF。
3.
(1)【解】①依据1:等腰三角形的两个底角相等(或等边对等角)。依据2:两角分别相等且其中一组等角的对边相等的两个三角形全等(或角角边或 AAS)。故答案为等腰三角形的两个底角相等(或等边对等角),两角分别相等且其中一组等角的对边相等的两个三角形全等(或角角边或 AAS)。
关键点拔:利用等量代换及等式的性质得出∠CBF= 是解题关键。
思路分析:
②另一种证法如下:如图
(1),连接 AD。
∵AB = AC,D 是 BC 的中点,
∴AD 是∠BAC 的平分线。
∵DE⊥AB,DF⊥AC,
∴DE = DF。(证法不唯一)

(2)【解】如图
(2),连接 AD。
∵AB = AC,D 是 BC 的中点,
∴AD 是∠BAC 的平分线。
∵DE⊥AB,DF⊥AC,
∴DE = DF。
∵S△ABC = S△ABD + S△ACD,
∴$\frac{1}{2}$×AB×CG = $\frac{1}{2}$×AB×DE + $\frac{1}{2}$×AC×DF,
∴CG = 2DE,故答案为 CG = 2DE。

(3)【证明】(任选一个证明即可)选择①:
∵DE,DF 分别是△ABD 和△ACD 的中线,
∴BE = $\frac{1}{2}$AB,CF = $\frac{1}{2}$AC。
∵AB = AC,
∴BE = CF,∠B = ∠C。又
∵D 是 BC 的中点,
∴BD = CD。在△BDE 与△CDF 中,$\begin{cases}BE = CF\\∠B = ∠C\\BD = CD\end{cases}$,
∴△BDE≌△CDF(SAS),
∴DE = DF。
选择②:
∵AB = AC,D 是 BC 的中点,
∴∠B = ∠C,BD = CD,AD⊥BC,
∴∠ADB = ∠ADC = 90°。又
∵DE,DF 分别是△ABD 和△ACD 的角平分线,
∴∠BDE = ∠CDF = 45°。在△BDE 与△CDF 中,$\begin{cases}∠B = ∠C\\BD = CD\\∠BDE = ∠CDF\end{cases}$,
∴△BDE≌△CDF(ASA),
∴DE = DF。
查看更多完整答案,请扫码查看


