《2025年初中必刷题八年级数学上册人教版》

10 如图,已知点$P(2m - 1,6m - 5)在第一象限角平分线OC$上,一直角顶点与点$P$重合,角的两边与$x$轴、$y轴分别交于A$点,$B$点,则：
(1)点$P$的坐标为____；
(2)$OA + BO= $____.

答案：

(1)(1,1)
(2)2 【解析】
(1)如图,作 PE⊥y 轴于点 E,PF⊥x轴于点 F. 根据题意,得PE=PF,
∴2m-1=6m-5,解得 m=1,
∴P(1,1).
(2)由
(1)得∠EPF=90°,PE=PF=1.
∵∠BPA=90°,
∴∠EPB=∠FPA.在△BEP 和△AFP 中,$\left\{\begin{array}{l} ∠PEB=∠PFA,\\ PE=PF,\\ ∠EPB=∠FPA,\end{array}\right.$
∴△BEP≌△AFP(ASA),
∴BE=AF,
∴OA+OB=OF+AF+OE-BE=OF+OE,
∴OA+BO=2.

11 [2024福建福州期中]如图,$\triangle ABC$中,$BC= 10$,$AC - AB= 5$,$AD是\angle BAC$的平分线,$CD\perp AD$,则$S_{\triangle BDC}$的最大值为____.

答案：
12.5 【解析】如图,延长AB,CD 交于点 E.
∵AD平分∠BAC,
∴∠CAD=∠EAD.
∵CD⊥AD,
∴∠ADC=∠ADE=90°.在△ADE 和△ADC 中,$\left\{\begin{array}{l} ∠ADE=∠ADC,\\ AD=AD,\\ ∠EAD=∠CAD,\end{array}\right.$
∴△ADE≌△ADC(ASA),
∴AC=AE,DE=CD.
∵AC-AB=5,
∴AE-AB=5,即 BE=5.
∵DE=DC,
∴$S_{△BDC}=\frac{1}{2}S_{△BCE}$,
∴当 BE⊥BC时,$S_{△BEC}$取最大值,即$S_{△BDC}$取最大值,此时$S_{△BDC}=\frac{1}{2}×\frac{1}{2}×10×5=12.5$.故答案为 12.5.

12 [2025河北秦皇岛期中]如图,在$\triangle ABC$中,$D是AC$上一点($CD＞AD$).
(1)连接$BD$,作$\triangle DEF$(点$E在线段CD$上,点$F在线段AC$的右侧),使得$\triangle DEF\cong\triangle DAB$；(保留作图痕迹,不写作法)
(2)作图依据是____.

答案：
【解】
(1)如图,△DEF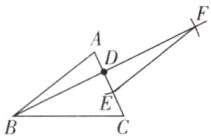 即为所求.
(2)在△DEF 和△DAB 中,$\left\{\begin{array}{l} DE=DA,\\ ∠EDF=∠ADB,\\ DF=DB,\end{array}\right.$
∴△DEF≌△DAB(SAS).故答案为 SAS(答案不唯一,与
(1)的作图痕迹对应即可).
思路分析
(1)作 PE⊥y 轴于 E,PF⊥x轴于 F.由角平分线的性质得出 PE=PF,进而得出方程 2m-1=6m-5,解方程求出 m=1,即可得出 P 点坐标;
(2)由 ASA 证明△BEP≌△AFP,得出 BE=AF,则 OA+OB=OE+OF=2.

13 如图,$\triangle ABC和\triangle DEF$,点$E$,$F在直线BC$上,$AB= DF$,$\angle A= \angle D$,$\angle ABC= \angle DFE$. 如图(1),易证：$BC + BE= BF$. 请解答下列问题：
(1)如图(2)、图(3),请猜想$BC$,$BE$,$BF$之间的数量关系,并直接写出猜想结论；
(2)请选择(1)中任意一种结论进行证明.

答案：
(1)【解】图
(2):BC+BE=BF,图
(3):BE-BC=BF.
(2)【证明】图
(2):
∵AB=DF,∠A=∠D,∠B=∠F,
∴△ABC≌△DFE(ASA),
∴BC=EF.
∵BE=BC+CE,
∴BC+BE=EF+BC+CE=BF.
图
(3):
∵AB=DF,∠A=∠D,∠ABC=∠DFE,
∴△ABC≌△DFE(ASA),
∴BC=EF.
∵BE=BF+EF,
∴BE-BC=BF+EF-BC=BF+BC-BC=BF.(任选一种回答即可)

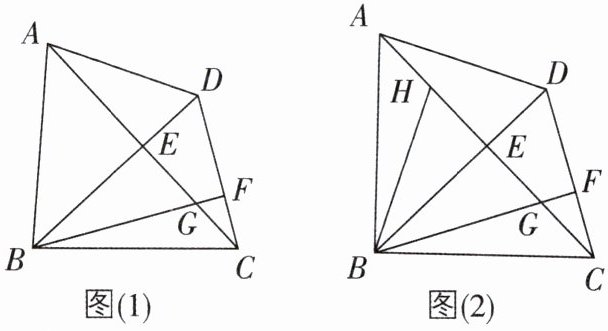
14 已知在四边形$ABCD$中,对角线$AC$,$BD相交于点E$,且$AC\perp BD$,作$BF\perp CD$,垂足为$F$,$BF与AC交于点G$,$\angle BGE= \angle ADE$.
(1)如图(1),求证：$AD= CD$；
(2)如图(2),$BH是\triangle ABE$的中线,若$AE= 2DE$,$DE= EG$,在不添加任何辅助线的情况下,请直接写出图(2)中四个三角形,使写出的每个三角形的面积都等于$\triangle ADE$面积的2倍.

答案：
(1)【证明】
∵∠BGE=∠ADE,∠BGE=∠CGF,
∴∠ADE=∠CGF.
∵AC⊥BD,BF⊥CD,
∴∠ADE+∠DAE=∠CGF+∠GCF=90°,
∴∠DAE=∠GCF.在△ADE 和△CDE 中,$\left\{\begin{array}{l} ∠DAE=∠DCE,\\ ∠AED=∠CED,\\ DE=DE,\end{array}\right.$
∴△ADE≌△CDE(AAS),
∴AD=CD.
(2)【解】面积等于△ADE 面积的 2 倍的三角形有△ACD,△ABE,△BCE,△BHG.设DE=a,则 AE=2DE=2a,EG=DE=a,
∴$S_{△ADE}=\frac{1}{2}AE\cdot DE=\frac{1}{2}\cdot2a\cdot a=a^{2}$.
∵BH是△ABE 的中线,
∴AH=HE=a.
∵AC⊥BD,
∴∠AED=∠CED=90°.
∵AD=CD,DE=DE,
∴Rt△ADE≌Rt△CDE(HL),
∴CE=AE=2a,则$S_{△ADC}=\frac{1}{2}AC\cdot DE=\frac{1}{2}\cdot(2a+2a)\cdot a=2a^{2}=2S_{△ADE}$.在△ADE 和△BGE 中,$\left\{\begin{array}{l} ∠AED=∠BEG,\\ DE=GE,\\ ∠ADE=∠BGE,\end{array}\right.$
∴△ADE≌△BGE(ASA),
∴BE=AE=2a,
∴$S_{△ABE}=\frac{1}{2}AE\cdot BE=\frac{1}{2}\cdot2a\cdot2a=2a^{2}=2S_{△ADE}$,$S_{△BCE}=\frac{1}{2}CE\cdot BE=\frac{1}{2}\cdot2a\cdot2a=2a^{2}=2S_{△ADE}$,$S_{△BHG}=\frac{1}{2}HG\cdot BE=\frac{1}{2}\cdot(a+a)\cdot2a=2a^{2}=2S_{△ADE}$.综上所述,面积等于△ADE 面积的 2 倍的三角形有△ACD,△ABE,△BCE,△BHG.
关键点拨
(2)设 DE=a,用含 a 的代数式表示出各相关线段的长,易证$S_{△ADC}=S_{△ABE}=S_{△BCE}=S_{△BHG}=2a^{2}=2S_{△ADE}$.