第62页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
二、填空题(本大题共4小题,每小题5分,共20分)
10[2025北京西城区期末]如图,在3×3的正方形网格中有四个格点A,B,C,D,以其中一个点为原点,网格线所在直线为坐标 轴(水平向右为x轴正方向,竖直向上为y轴正方向),建立平面直角坐标系,使其余三个点中存在两个点关于一条坐标轴对称,则原点可能是点______.
轴(水平向右为x轴正方向,竖直向上为y轴正方向),建立平面直角坐标系,使其余三个点中存在两个点关于一条坐标轴对称,则原点可能是点______.
10[2025北京西城区期末]如图,在3×3的正方形网格中有四个格点A,B,C,D,以其中一个点为原点,网格线所在直线为坐标
 轴(水平向右为x轴正方向,竖直向上为y轴正方向),建立平面直角坐标系,使其余三个点中存在两个点关于一条坐标轴对称,则原点可能是点______.
轴(水平向右为x轴正方向,竖直向上为y轴正方向),建立平面直角坐标系,使其余三个点中存在两个点关于一条坐标轴对称,则原点可能是点______.
答案:
10. D [解析]如图所示,点A与点B关于x轴对称,原点是点D。故答案为D。

10. D [解析]如图所示,点A与点B关于x轴对称,原点是点D。故答案为D。

11小曹同学复习时将几种三角形的关系整理如图,则“?”处的条件可以是
∠A=60°(答案不唯一)
.(填一个即可)
答案:
11. ∠A=60°(答案不唯一) [解析]添加∠A=60°。理由如下:
∵△ABC为等腰三角形,∠A=60°,
∴∠B=∠C=(180° - ∠A)/2=60°,
∴△ABC为等边三角形,故答案为∠A=60°(答案不唯一)。
∵△ABC为等腰三角形,∠A=60°,
∴∠B=∠C=(180° - ∠A)/2=60°,
∴△ABC为等边三角形,故答案为∠A=60°(答案不唯一)。
12若$(a-3)^{2}+\sqrt{b-5}= 0,$则以a,b为边长的等腰三角形的周长为______
11或13
.
答案:
12. 11或13 [解析]
∵(a - 3)²+√(b - 5)=0,
∴a=3,b=5。当a=3为腰时,三角形周长为2a + b=6 + 5=11;当b=5为腰时,三角形的周长为a + 2b=3 + 10=13,故答案为11或13。
∵(a - 3)²+√(b - 5)=0,
∴a=3,b=5。当a=3为腰时,三角形周长为2a + b=6 + 5=11;当b=5为腰时,三角形的周长为a + 2b=3 + 10=13,故答案为11或13。
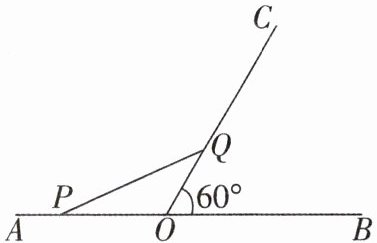
13如图,∠BOC= 60°,点A是OB反向延长线上的一点,OA= 10cm,动点P从点A出发沿AB以2cm/s的速度移动,动点Q从点O出发沿OC以1cm/s的速度移动,如果P,Q同时出发,用t s表示移动的时间,当t= ______时,△POQ是等腰三角形.

答案:
13. $\frac {10}{3}$或10 [解析]当P在OA上,PO=QO时,△POQ是等腰三角形,如图
(1)所示。
∵PO=AO - AP=(10 - 2t)cm,OQ=t cm,
∴当PO=QO时,10 - 2t=t,解得t=$\frac{10}{3}$。当P在OB上,PO=QO时,△POQ是等腰三角形,如图
(2)所示。
∵PO=AP - AO=(2t - 10)cm,OQ=t cm,
∴当PO=QO时,2t - 10=t,解得t=10。
易错警示:当△POQ是等腰三角形时,需分情况讨论:①当点P在OA上时,PO=OQ;②当点P在OB上时,PO=OQ。
故当t=$\frac {10}{3}$或10时,△POQ是等腰三角形。
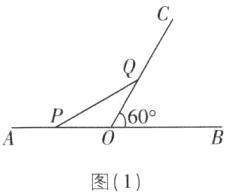

13. $\frac {10}{3}$或10 [解析]当P在OA上,PO=QO时,△POQ是等腰三角形,如图
(1)所示。
∵PO=AO - AP=(10 - 2t)cm,OQ=t cm,
∴当PO=QO时,10 - 2t=t,解得t=$\frac{10}{3}$。当P在OB上,PO=QO时,△POQ是等腰三角形,如图
(2)所示。
∵PO=AP - AO=(2t - 10)cm,OQ=t cm,
∴当PO=QO时,2t - 10=t,解得t=10。
易错警示:当△POQ是等腰三角形时,需分情况讨论:①当点P在OA上时,PO=OQ;②当点P在OB上时,PO=OQ。
故当t=$\frac {10}{3}$或10时,△POQ是等腰三角形。


14[2025山西吕梁期中]如图,在△ABC中,AB= AC,∠A= 36°.
(1)尺规作图:作线段AB的垂直平分线,交AB于点E,交AC于点D,连接BD.(不必写作图步骤,保留作图痕迹)
(2)求证:BD= BC.
(1)尺规作图:作线段AB的垂直平分线,交AB于点E,交AC于点D,连接BD.(不必写作图步骤,保留作图痕迹)
(2)求证:BD= BC.

答案:
14.
(1)【解】如图。
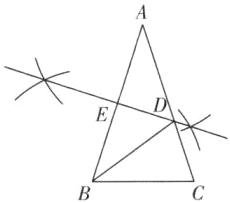
(2)【证明】
∵AB=AC,∠A=36°,
∴∠ABC=∠C=$\frac {1}{2}$(180° - ∠A)=72°。
∵DE是AB的垂直平分线,
∴AD=BD,
∴∠ABD=∠A=36°,
∴∠BDC=∠A+∠ABD=36°+36°=72°=∠C,
∴BD=BC。
14.
(1)【解】如图。

(2)【证明】
∵AB=AC,∠A=36°,
∴∠ABC=∠C=$\frac {1}{2}$(180° - ∠A)=72°。
∵DE是AB的垂直平分线,
∴AD=BD,
∴∠ABD=∠A=36°,
∴∠BDC=∠A+∠ABD=36°+36°=72°=∠C,
∴BD=BC。
15[2025江苏无锡质检]在如图所示的由小正方形组成的网格中建立平面直角坐标系,已知△ABC的顶点都在小正方形的顶点上.
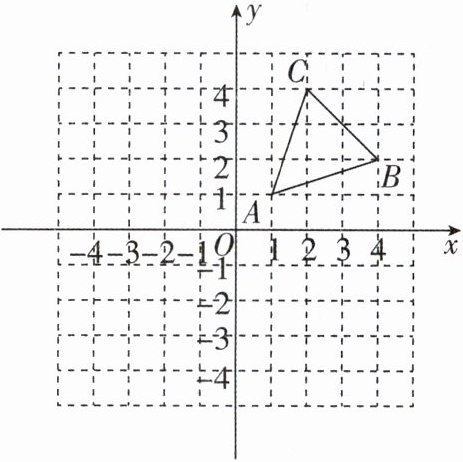
(1)△ABC三个顶点的坐标分别为A______,B______,C______.
(2)借助网格,请只用直尺(不含刻度)在x轴上找一点Q,使得△QAB的周长最小(在图中标出点Q),此时点Q的坐标为______.

(1)△ABC三个顶点的坐标分别为A______,B______,C______.
(2)借助网格,请只用直尺(不含刻度)在x轴上找一点Q,使得△QAB的周长最小(在图中标出点Q),此时点Q的坐标为______.
答案:
15. 【解】
(1)根据题图得A(1,1),B(4,2),C(2,4),故答案为(1,1),(4,2),(2,4)。
(2)如图,作点B关于x轴对称的点B',连接AB',交x轴于Q,则点Q即为所求,点Q的坐标为(2,0)。故答案为(2,0)。

15. 【解】
(1)根据题图得A(1,1),B(4,2),C(2,4),故答案为(1,1),(4,2),(2,4)。
(2)如图,作点B关于x轴对称的点B',连接AB',交x轴于Q,则点Q即为所求,点Q的坐标为(2,0)。故答案为(2,0)。

16[2024辽宁丹东期末]如图,点O是等边△ABC内一点,D是△ABC外的一点,∠AOB= 110°,∠BOC= α,△BOC≌△ADC,∠OCD= 60°,连接OD.
(1)求证:△OCD是等边三角形.
(2)当α= 150°时,试判断△AOD的形状,并说明理由.
(3)探究:当α为多少度时,△AOD是等腰三角形?
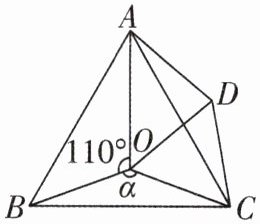
(1)求证:△OCD是等边三角形.
(2)当α= 150°时,试判断△AOD的形状,并说明理由.
(3)探究:当α为多少度时,△AOD是等腰三角形?

答案:
16.
(1)【证明】
∵△BOC≌△ADC,
∴OC=DC。
∵∠OCD=60°,
∴△OCD是等边三角形。
【解】
(2)△AOD是直角三角形。理由如下:
∵△OCD是等边三角形,
∴∠ODC=60°。
∵△BOC≌△ADC,α=150°,
∴∠ADC=∠BOC=α=150°,
∴∠ADO=∠ADC - ∠ODC=150° - 60°=90°,
∴△AOD是直角三角形。
(3)
∵△OCD是等边三角形,
∴∠COD=∠ODC=60°。
∵∠AOB=110°,∠ADC=∠BOC=α,
∴∠AOD=360° - ∠AOB - ∠BOC - ∠COD=360° - 110° - α - 60°=190° - α,∠ADO=∠ADC - ∠ODC=α - 60°,
∴∠OAD=180° - ∠AOD - ∠ADO=180°-(190° - α)-(α - 60°)=50°。分三种情况:①当∠AOD=∠ADO时,190° - α=α - 60°,
∴α=125°。②当∠AOD=∠OAD时,190° - α=50°,
∴α=140°。③当∠ADO=∠OAD时,α - 60°=50°,
∴α=110°。综上所述,当α=110°或125°或140°时,△AOD是等腰三角形。
(1)【证明】
∵△BOC≌△ADC,
∴OC=DC。
∵∠OCD=60°,
∴△OCD是等边三角形。
【解】
(2)△AOD是直角三角形。理由如下:
∵△OCD是等边三角形,
∴∠ODC=60°。
∵△BOC≌△ADC,α=150°,
∴∠ADC=∠BOC=α=150°,
∴∠ADO=∠ADC - ∠ODC=150° - 60°=90°,
∴△AOD是直角三角形。
(3)
∵△OCD是等边三角形,
∴∠COD=∠ODC=60°。
∵∠AOB=110°,∠ADC=∠BOC=α,
∴∠AOD=360° - ∠AOB - ∠BOC - ∠COD=360° - 110° - α - 60°=190° - α,∠ADO=∠ADC - ∠ODC=α - 60°,
∴∠OAD=180° - ∠AOD - ∠ADO=180°-(190° - α)-(α - 60°)=50°。分三种情况:①当∠AOD=∠ADO时,190° - α=α - 60°,
∴α=125°。②当∠AOD=∠OAD时,190° - α=50°,
∴α=140°。③当∠ADO=∠OAD时,α - 60°=50°,
∴α=110°。综上所述,当α=110°或125°或140°时,△AOD是等腰三角形。
查看更多完整答案,请扫码查看


