第21页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
下列各项中,两个图形属于全等形的是(
C
)
答案:
C 【解析】能够完全重合的两个图形叫作全等形.只有 C 选项中的两个图形能够完全重合,是全等形,故选 C.
2 [2025重庆巴南区期中]下列说法正确的是( )
A.周长相等的两个三角形是全等三角形
B.形状、大小相同的两个三角形是全等三角形
C.面积相等的两个三角形是全等三角形
D.所有的等边三角形都是全等三角形
A.周长相等的两个三角形是全等三角形
B.形状、大小相同的两个三角形是全等三角形
C.面积相等的两个三角形是全等三角形
D.所有的等边三角形都是全等三角形
答案:
B 【解析】根据全等三角形的定义能够判断出 B 选项的说法正确,A、C、D 选项的反例如下;

B 【解析】根据全等三角形的定义能够判断出 B 选项的说法正确,A、C、D 选项的反例如下;

如图所示的两个三角形全等,则∠E的度数为(
A.$80^{\circ}$
B.$70^{\circ}$
C.$60^{\circ}$
D.$50^{\circ}$
B
)A.$80^{\circ}$
B.$70^{\circ}$
C.$60^{\circ}$
D.$50^{\circ}$
答案:
B 【解析】由题可知△ABC≌△FED,
∴∠E=∠B=180° - 44° - 66°=70°,故选 B.
∴∠E=∠B=180° - 44° - 66°=70°,故选 B.
4 [2025浙江宁波期末]如图,$\triangle ABC \cong \triangle ADE$,点A,B,E在同一条直线上,$AC = 6$,$BE = 2$,则AB的长为(
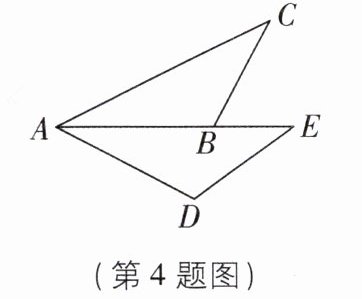
A.2
B.4
C.6
D.8
B
)
A.2
B.4
C.6
D.8
答案:
B 【解析】
∵△ABC≌△ADE,AC=6,
∴AE = AC=6.
∵BE=2,
∴AB=AE - BE=6 - 2=4,故选 B.
∵△ABC≌△ADE,AC=6,
∴AE = AC=6.
∵BE=2,
∴AB=AE - BE=6 - 2=4,故选 B.
5 如图,在平面直角坐标系中,$\triangle OAB的顶点坐标分别是A(-6,0)$,$B(0,5)$,$\triangle OA'B' \cong \triangle AOB$,若点$A'$在x轴上,则点$B'$的坐标是
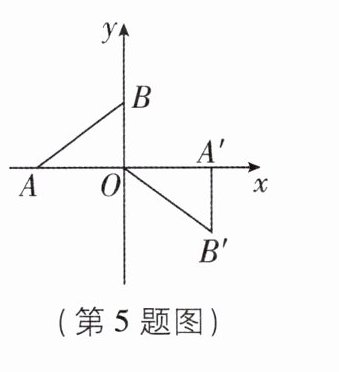
(6, - 5)
.
答案:
(6, - 5) 【解析】
∵A( - 6,0),B(0,5),
∴OA = 6,OB=5,∠AOB=90°.
∵△OA'B'≌△AOB,
∴OA'=OA=6,A'B'=OB=5,∠B'A'O=90°.
∵点 B'在第四象限,
∴点 B'的坐标是(6, - 5).
∵A( - 6,0),B(0,5),
∴OA = 6,OB=5,∠AOB=90°.
∵△OA'B'≌△AOB,
∴OA'=OA=6,A'B'=OB=5,∠B'A'O=90°.
∵点 B'在第四象限,
∴点 B'的坐标是(6, - 5).
6 如图,点B,C,D在同一条直线上,$\angle B = \angle D = 90^{\circ}$,$\triangle ABC \cong \triangle CDE$,$AB = 6$,$BC = 8$,$CE = 10$.
(1)求$\triangle ABC$的周长;
(2)求$\triangle ACE$的面积.
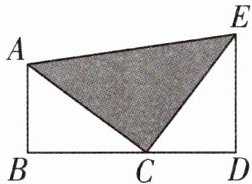
(1)求$\triangle ABC$的周长;
(2)求$\triangle ACE$的面积.

答案:
【解】
(1)
∵△ABC≌△CDE,CE=10,
∴AC = CE=10.
∵AB=6,BC=8,
∴△ABC 的周长为AB+BC+AC=6+8+10=24.
(2)
∵∠B=90°,
∴∠ACB+∠BAC=90°.
∵△ABC≌△CDE,
∴∠ECD=∠CAB,
∴∠ACB+∠ECD=90°,
∴∠ACE=90°.
∵AC=CE=10,
∴△ACE 的面积为$\frac{1}{2}$AC·CE=$\frac{1}{2}$×10×10=50.
(1)
∵△ABC≌△CDE,CE=10,
∴AC = CE=10.
∵AB=6,BC=8,
∴△ABC 的周长为AB+BC+AC=6+8+10=24.
(2)
∵∠B=90°,
∴∠ACB+∠BAC=90°.
∵△ABC≌△CDE,
∴∠ECD=∠CAB,
∴∠ACB+∠ECD=90°,
∴∠ACE=90°.
∵AC=CE=10,
∴△ACE 的面积为$\frac{1}{2}$AC·CE=$\frac{1}{2}$×10×10=50.
7 一个三角形的三条边的长分别是5,8,10,另一个三角形的三条边的长分别是5,$4x + 2$,$2y - 2$,若这两个三角形全等,则$x + y$的值是______
7.5 或 7
.
答案:
7.5 或 7 【解析】
∵两个三角形全等,
∴当4x+2=8,2y - 2=10 时,解得 x=1.5,y=6,此时 x+y=7.5;当4x+2=10,2y - 2=8 时,解得x=2,y=5,此时 x+y=7.综上,x+y 的值是7.5或7,故答案为7.5或7.
易错警示 注意全等三角形中边与边之间的对应关系.本题中有两种对应关系,故会产生两个点 D 的坐标,不要漏解.
易错警示 当两个全等三角形的对应角的对应关系未定时,需分情况讨论.
∵两个三角形全等,
∴当4x+2=8,2y - 2=10 时,解得 x=1.5,y=6,此时 x+y=7.5;当4x+2=10,2y - 2=8 时,解得x=2,y=5,此时 x+y=7.综上,x+y 的值是7.5或7,故答案为7.5或7.
易错警示 注意全等三角形中边与边之间的对应关系.本题中有两种对应关系,故会产生两个点 D 的坐标,不要漏解.
易错警示 当两个全等三角形的对应角的对应关系未定时,需分情况讨论.
查看更多完整答案,请扫码查看


