第89页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
一、选择题(本大题共5小题,每小题5分,共25分)
1 [2025江苏无锡惠山区期中]下列分解因式正确的是(
A.$-2x^{2}+4x= -2x(x + 2)$
B.$x^{2}+xy + x = x(x + y)$
C.$x(x - y)-y(x - y)= (x - y)^{2}$
D.$x^{2}+6x - 9= (x - 3)^{2}$
1 [2025江苏无锡惠山区期中]下列分解因式正确的是(
C
)A.$-2x^{2}+4x= -2x(x + 2)$
B.$x^{2}+xy + x = x(x + y)$
C.$x(x - y)-y(x - y)= (x - y)^{2}$
D.$x^{2}+6x - 9= (x - 3)^{2}$
答案:
C 【解析】
A $-2x^{2}+4x=-2x(x-2)\neq-2x(x+2)$
B $x^{2}+xy+x=x(x+y+1)\neq x(x+y)$
C $x(x-y)-y(x-y)=(x-y)(x-y)=(x-y)^{2}$
D $x^{2}+6x-9\neq(x-3)^{2}$
A $-2x^{2}+4x=-2x(x-2)\neq-2x(x+2)$
B $x^{2}+xy+x=x(x+y+1)\neq x(x+y)$
C $x(x-y)-y(x-y)=(x-y)(x-y)=(x-y)^{2}$
D $x^{2}+6x-9\neq(x-3)^{2}$
2 [2025安徽安庆质检]多项式$a^{2}b + 4a^{2}b^{2}-2a^{3}b^{2}c$各项的公因式是( )
A.$2a^{2}b^{2}c$
B.$2a^{2}b$
C.$a^{2}b$
D.$4a^{3}b^{2}c$
A.$2a^{2}b^{2}c$
B.$2a^{2}b$
C.$a^{2}b$
D.$4a^{3}b^{2}c$
答案:
C 【解析】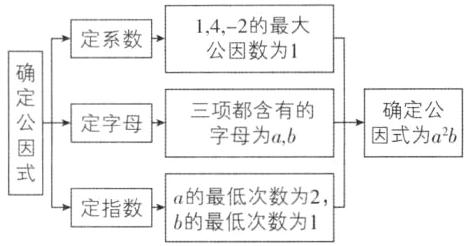
故选C.
C 【解析】

故选C.
3 已知$m^{2}+n^{2}= 25$,$mn = 12$,则$m^{3}n - mn^{3}$的值为(
A.$-84$
B.$84$
C.$\pm84$
D.$300$
C
)A.$-84$
B.$84$
C.$\pm84$
D.$300$
答案:
C 【解析】$\because m^{2}+n^{2}=25$,$mn=12$,$\therefore (m-n)^{2}=m^{2}+n^{2}-2mn=25-2×12=1$,$(m+n)^{2}=m^{2}+n^{2}+2mn=25+2×12=49$,$\therefore m-n=\pm1$,$m+n=\pm7$.当$m-n=1$,$m+n=7$时,$m^{3}n-mn^{3}=mn(m^{2}-n^{2})=mn(m+n)(m-n)=12×7×1=84$;当$m-n=1$,$m+n=-7$时,$m^{3}n-mn^{3}=mn(m^{2}-n^{2})=mn(m+n)(m-n)=12×(-7)×1=-84$;当$m-n=-1$,$m+n=7$时,$m^{3}n-mn^{3}=mn(m^{2}-n^{2})=mn(m+n)(m-n)=12×7×(-1)=-84$;当$m-n=-1$,$m+n=-7$时,$m^{3}n-mn^{3}=mn(m^{2}-n^{2})=mn(m+n)(m-n)=12×(-7)×(-1)=84$.故选C.
4 若$k$为任意整数,则$(2k + 3)^{2}-4k^{2}$的值总能(
A.被2整除
B.被3整除
C.被5整除
D.被7整除
B
)A.被2整除
B.被3整除
C.被5整除
D.被7整除
答案:
B 【解析】$\because (2k+3)^{2}-4k^{2}=(2k+3)^{2}-(2k)^{2}=(2k+3+2k)\cdot(2k+3-2k)=3(4k+3)$,$k$为任意整数,$\therefore$其值总能被3整除.故选B.
5 [2025浙江宁波镇海区质检]若关于$x的不等式组\begin{cases}x + m\leqslant4,\frac{x}{2}-\frac{x - 1}{4}>1\end{cases} $有解且至多有4个整数解,且多项式$x^{2}-(1 - m)$能在有理数范围内因式分解,则符合条件的整数$m$的个数为(
A.1
B.2
C.3
D.4
B
)A.1
B.2
C.3
D.4
答案:
B 【解析】$\because$不等式组$\begin{cases}x+m\leqslant4\\\dfrac{x}{2}-\dfrac{x-1}{4}>1\end{cases}$有解,$\therefore 3<x\leqslant4-m$.$\because$不等式组$\begin{cases}x+m\leqslant4\\\dfrac{x}{2}-\dfrac{x-1}{4}>1\end{cases}$有解且至多有4个整数解,$\therefore 3<4-m<8$,解得$-4<m<1$,$\therefore 0<1-m<5$.又$\because$多项式$x^{2}-(1-m)$能在有理数范围内因式分解,$\therefore 1-m=4$或$1-m=1$,$\therefore$符合条件的整数$m$的值为-3,0,即符合条件的整数$m$的个数为2.故选B.
二、填空题(本大题共3小题,每小题5分,共15分)
6 已知$m^{2}-2m - 2011 = 0$,则$m^{3}-m^{2}-2013m - 2014 = $
6 已知$m^{2}-2m - 2011 = 0$,则$m^{3}-m^{2}-2013m - 2014 = $
-3
.
答案:
-3 【解析】$\because m^{2}-2m-2011=0$,$\therefore m(m-2)=2011$.$m^{3}-m^{2}-2013m-2014=m^{3}-m^{2}-m^{2}+m^{2}-2013m-2014=m^{3}-2m^{2}+m^{2}-2013m-2014=m^{2}(m-2)+m(m-2013)-2014=m^{2}(m-2)+m(m-2-2011)-2014=m^{2}(m-2)+m(m-2)-2011m-2014$.把$m(m-2)=2011$代入上式,得原式$=2011m+2011-2011m-2014=-3$.故答案为-3.
7 [2025黑龙江哈尔滨期中]我们在学习许多代数公式时,可以用几何图形来推理验证. 观察图(1),$a^{2}-1 = a(a - 1)+(a - 1)= (a - 1)(a + 1)$. 接下来,观察图(2),通过类比思考,因式分解:$a^{3}-1 = $
$(a-1)(a^{2}+a+1)$
.
答案:
$(a-1)(a^{2}+a+1)$ 【解析】将题图
(2)分成三个长方体,可得体积为$a× a×(a-1)+1×1×(a-1)+1× a×(a-1)=a^{2}(a-1)+a(a-1)+(a-1)=(a-1)(a^{2}+a+1)$,$\therefore a^{3}-1=(a-1)(a^{2}+a+1)$.故答案为$(a-1)(a^{2}+a+1)$.
(2)分成三个长方体,可得体积为$a× a×(a-1)+1×1×(a-1)+1× a×(a-1)=a^{2}(a-1)+a(a-1)+(a-1)=(a-1)(a^{2}+a+1)$,$\therefore a^{3}-1=(a-1)(a^{2}+a+1)$.故答案为$(a-1)(a^{2}+a+1)$.
8 [2024广东深圳校级模拟]定义:任意两个数a,b,按规则c = a + b - ab扩充得到数c,称所得的数c为“鸿蒙数”. 若a = 2,b = x^{2}-2x + 2,c为由a,b扩充得到的“鸿蒙数”,则b,c的大小关系为b
$\geqslant$
c.
答案:
$\geqslant$ 【解析】由题意得,当$a=2$,$b=x^{2}-2x+2$时,$c=a+b-ab=2+(x^{2}-2x+2)-2(x^{2}-2x+2)=2+x^{2}-2x+2-2x^{2}+4x-4=-x^{2}+2x$,$\therefore b-c=(x^{2}-2x+2)-(-x^{2}+2x)=x^{2}-2x+2+x^{2}-2x=2x^{2}-4x+2=2(x^{2}-2x+1)=2(x-1)^{2}\geqslant0$,$\therefore b\geqslant c$.故答案为$\geqslant$.
9 把下列各式分解因式:
(1)$ax^{3}-16ax$;
(2)$(2x - 3y)^{2}-2x(2x - 3y)+x^{2}$;
(3)$(m^{2}+1)^{2}-4m^{2}$.
(1)$ax^{3}-16ax$;
(2)$(2x - 3y)^{2}-2x(2x - 3y)+x^{2}$;
(3)$(m^{2}+1)^{2}-4m^{2}$.
答案:
【解】
(1)原式$=ax(x^{2}-16)=ax(x+4)(x-4)$.
(2)原式$=(2x-3y-x)^{2}=(x-3y)^{2}$.
(3)原式$=(m^{2}+1+2m)(m^{2}+1-2m)=(m+1)^{2}(m-1)^{2}$.
(1)原式$=ax(x^{2}-16)=ax(x+4)(x-4)$.
(2)原式$=(2x-3y-x)^{2}=(x-3y)^{2}$.
(3)原式$=(m^{2}+1+2m)(m^{2}+1-2m)=(m+1)^{2}(m-1)^{2}$.
(1)观察图形,可以发现代数式$2m^{2}+5mn + 2n^{2}$可以因式分解为
(2)若每块小长方形的面积为$10\mathrm{cm}^{2}$,两块大正方形和两块小正方形的面积和为$58\mathrm{cm}^{2}$.
①试求$m + n$的值.
②图中所有裁剪线(虚线部分)长之和为
$(2m+n)(m+2n)$
.(2)若每块小长方形的面积为$10\mathrm{cm}^{2}$,两块大正方形和两块小正方形的面积和为$58\mathrm{cm}^{2}$.
①试求$m + n$的值.
【解】依题意得,$2m^{2}+2n^{2}=58$,$mn=10$,$\therefore m^{2}+n^{2}=29$,$\therefore (m+n)^{2}=m^{2}+n^{2}+2mn=29+20=49$.$\because m+n>0$,$\therefore m+n=7$.
②图中所有裁剪线(虚线部分)长之和为
42
$\mathrm{cm}$.
答案:
【解】
(1)由图形可知,$2m^{2}+5mn+2n^{2}=(2m+n)(m+2n)$.故答案为$(2m+n)(m+2n)$.
(2)①依题意得,$2m^{2}+2n^{2}=58$,$mn=10$,$\therefore m^{2}+n^{2}=29$,$\therefore (m+n)^{2}=m^{2}+n^{2}+2mn=29+20=49$.$\because m+n>0$,$\therefore m+n=7$.
②所有裁剪线长之和为$7×6=42(\text{cm})$.故答案为42.
(1)由图形可知,$2m^{2}+5mn+2n^{2}=(2m+n)(m+2n)$.故答案为$(2m+n)(m+2n)$.
(2)①依题意得,$2m^{2}+2n^{2}=58$,$mn=10$,$\therefore m^{2}+n^{2}=29$,$\therefore (m+n)^{2}=m^{2}+n^{2}+2mn=29+20=49$.$\because m+n>0$,$\therefore m+n=7$.
②所有裁剪线长之和为$7×6=42(\text{cm})$.故答案为42.
查看更多完整答案,请扫码查看


