《2025年初一入学分班必刷卷六年级数学》

14. (抽屉原理)衣柜中有三种不同颜色的手套各 3 双,在黑暗中从衣柜中取出手套,为确保能取得一双颜色相同且左、右相配对的一双手套,至少要取10只手套。

答案： 10 【解析】先将3种不同颜色的手套都取3只，即3只左手或3只右手，再任取1只，一定能左右配对。所以只要取$3×3 + 1 = 10$(只)就可以保证取到一双左右配对的同色手套。

15. (沏茶问题)小亮下午放学回家煮饭,淘米要 3 分钟,煮饭要 25 分钟,洗菜要 7 分钟,切菜要 4 分钟,炒菜要 10 分钟,如果煮饭和炒菜用不同的锅和炉子,小亮要把饭、菜都烧好,最少要28分钟。

答案： 28 【解析】先淘米，然后煮饭，煮饭的同时洗菜、切菜、炒菜，时间最省为$3 + 25 = 28$(分钟)。

16. (代换问题)某小学组织六年级学生春游。学校买了 182 瓶汽水分给学生,如果每 5 个空瓶又可换 1 瓶汽水,那么这些汽水瓶最多可换得45瓶汽水。

答案： 45 【解析】根据题意，5个空瓶可以换一瓶汽水，第一次：$182÷5 = 36$(瓶)……2(个)，第二次：$(36 + 2)÷5 = 7$(瓶)……3(个)，第三次：$(7 + 3)÷5 = 2$(瓶)，可换到$36 + 7 + 2 = 45$(瓶)。

17. (逻辑推理)如图是一把游戏锁,上面有 16 个按钮,游戏规则如下:按照按钮上的提示,按遍全部按钮,才能把锁打开。比如,当你按下第 1 行的第 2 个按钮"右 2"时,就要按照提示,向右移动 2 格按"下 2"钮,再按照提示按"下 1"钮……为了打开这把游戏锁,请你选择第一次应按的按钮,它在第 行的第 个。

答案：
2 3 【解析】如图，从可以得到“开”这个键的位置开始逆推，只有“左2”可以得到“开”这个键，再找出可以得到“左2”的键，只有“上2”……依次找出最后的位置是第2行第3列的“右1”。

18. (逻辑推理)甲、乙、丙三个同学中有一个人在同学们都不在时把教室打扫干净,事后老师问他们是谁做的好事,甲说:"是乙干的。"乙说:"不是我干的。"丙说:"不是我干的。"如果他们中有两人说了谎话,一个人说的是真话,由此断定是丙干的。

答案： 丙 【解析】假设甲说的是真话，那么是乙干的，这时丙说的话是真话，与只有一人说真话产生矛盾，因此甲说的是假话，即不是乙干的，所以乙说的是真话，从而丙说的是假话，故是丙干的。

19. (抽屉原理)王叔叔只记得李叔叔的电话号码是 76045□□,还记得最大数字是 7,各个数字又不重复,王叔叔要拨通李叔叔的电话,最多要试打6次。

答案： 6 【解析】根据题意，最大数字是7，各个数字又不重复，那么剩下的两个数字只能是1，2，3中的两个，倒数第二位有3种可能，倒数第一位剩2种可能，因此最多试打$3×2 = 6$(次)。

20. (逻辑推理)爸爸给女儿优优买了一个(圆柱形的)生日蛋糕,优优想把蛋糕切成大小不一定相等的若干块(不少于 10 块)分给 10 个小朋友,若设沿竖直方向切分这块蛋糕,至少需要切 刀。

答案：
4 【解析】要想切的刀数尽量少，就要求每一刀都切出尽量多的块数。把一整个蛋糕看成一块，第一刀切开变成两块，增加了一块，第二刀最多变成4块，在第一刀的基础上增加了2块，并且可以发现，第n刀最多增加n块，所以切n刀，蛋糕的块数最多就是$1 + 1 + 2 + 3 +... + n$块。当$n = 4$的时候，蛋糕的块数为11块，满足题目要求。

1. (计数原理)某条铁路线上,包括起点和终点在内原来共有 7 个车站,现在新增了 3 个车站,铁路上两站之间往返的车票不一样,这样需要增加不同的车票(C)
A.24 种
B.42 种
C.48 种
D.21 种

答案： C 【解析】新增车站前共有车票$(1 + 2 + 3 +... + 6)×2 = 42$(种)，新增车站后共有车票$(1 + 2 + 3 +... + 9)×2 = 90$(种)，需要增加$90 - 42 = 48$(种)。

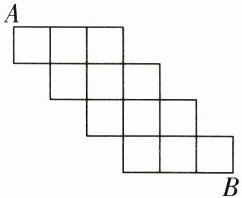
2. (排列组合)某街道分布示意图如图所示,一个居民从 A 处前往 B 处,若规定只能走从左到右或从上到下的方向,这样该居民可选择的不同路线共有( )


A.119 条
B.121 条
C.123 条
D.125 条

答案：
B514274040144181B121【解析】如解图所示，从A点开始，把到达每个路口的路径条数标记出来，每个小正方形右下角的数字等于左下角和右上角两个数字之和，直到求出到达B点所能选择的路线条数。

3. (排列组合)某市举办的名校足球联谊比赛,共有 A,B,C,D,E,F 六支足球队参加,已知最终比赛结果中,A 的排名高于 B,B 的排名高于 C,D 的排名高于 E,E 的排名高于 F,无排名相同的结果,则符合这种情况的所有比赛排名有(B)
A.12 种
B.20 种
C.36 种
D.50 种

答案： B 【解析】根据题意可知获得小组第一名的球队只能是A队或D队，假设A队是第一名，那么可能的排名为ABCDEF，ABDCEF，ABDECF，ABDEFC，ADBCEF，ADBECF，ADBEFC，ADEBCF，ADEBFC，ADEBCF；假设D队为第一名，那么可能的排名为DEFABC，DEAFBC，DEABFC，DEABCF，DABCEF，DABECF，DABEFC，DAEFBC，DAEBFC，DAEBCF，共计20种情况。

4. (容斥原理)同学们去春游,带水壶的有 80 人,带水果的有 70 人,两样都没带的有 6 人,若两样都带的人数是所有参加春游人数的一半,则参加春游的同学人数是(B)
A.102
B.104
C.106
D.108

答案： B 【解析】设两样都带的同学有n人，则参加春游的同学共2n人，只带水壶的同学有$(80 - n)$人，只带水果的同学有$(70 - n)$人，根据题意可得$n + (80 - n) + (70 - n) + 6 = 2n$，解得$n = 52$，所以参加春游的同学共有$52×2 = 104$(人)。