《2025年初一入学分班必刷卷六年级数学》

1. (植树问题)把一根木料锯成3段要3.6分钟,锯成8段要12.6分钟。(每段所需时间一样)

答案： 12.6 【解析】根据题意可知,锯木次数=段数-1。所以锯成3段,要锯3-1=2(次),每次需要3.6÷2=1.8(分钟),锯8段,要锯8-1=7(次),需要1.8×7=12.6(分钟)。

2. (圆柱与圆锥)若圆柱与圆锥的体积与底面积都相等,圆柱的高是12厘米,圆锥的高是______厘米。
36

答案： 36 【解析】因为等底等高的圆柱体积是圆锥的3倍,故体积和底面积相等时圆锥的高是圆柱的3倍,圆柱的高是12厘米,则圆锥的高是12×3=36(厘米)。

3. (工程问题)一项工程,如果由甲、乙合做需要8天完成,现由甲先做3天,乙再做5天,才完成工程的$\frac {7}{16}$,如果由乙单独做,需32天完成。

答案： 32 【解析】将总的工作量看作单位“1”,所以甲、乙两人合做的工效为$\frac{1}{8}$,甲做3天,乙做5天,完成$\frac{7}{16}$,相当于甲、乙合做3天后乙独做2天完成$\frac{7}{16}$,则可计算得到乙的工效为$(\frac{7}{16}-\frac{3}{8})÷2=\frac{1}{32}$,则乙单独做需要$1÷\frac{1}{32}=32$(天)完成。

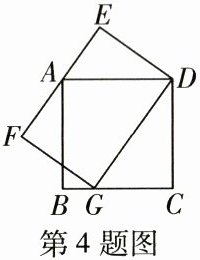
4. (等积转换)如图,正方形ABCD的边长是6厘米,长方形DEFG的边EF过点A,点G在BC上,且$DG= 8$厘米,长方形的宽DE为______厘米。

答案：
4.5 【解析】如解图,连接AG,因为△ADG的面积=$\frac{1}{2}×AD×AB=\frac{1}{2}×6×6=18$(平方厘米),若以DG为底时,则△ADG的面积=$\frac{1}{2}×DE×DG$,即$\frac{1}{2}×DE×8=18$,解得DE=4.5。

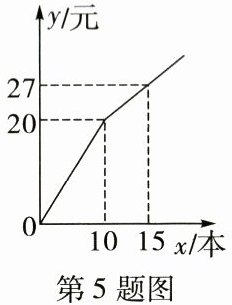
5. (变量间的关系)小明到超市买练习本,超市正在打折促销:购买10本以上,从第11本开始按标价打折优惠,买练习本所花费的钱数y(元)与练习本的本数x(本)之间的关系如图所示,那么在这个超市买10本以上的练习本优惠折扣是______折。

七

答案： 七 【解析】打折前,每本练习本的价格为20÷10=2(元),打折后,每本练习本的价格为(27-20)÷(15-10)=1.4(元),1.4÷2=0.7,所以,在这个超市买10本以上的练习本优惠折扣是七折。

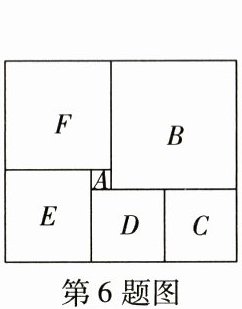
6. (可能性)如图,是一块在电脑屏幕上出现的长方形色块,由A、B、C、D、E、F六个正方形组成,已知中间最小的正方形A的边长为1。现在将鼠标随机指向这个长方形色块,那么鼠标落在正方形A的可能性的大小为______$\frac{1}{143}$。

答案： $\frac{1}{143}$【解析】设D,C正方形的边长为x,依次可得E正方形的边长为x+1,F正方形的边长为x+2,B正方形的边长为x+3,则有$x+x+x+1=x+2+x+3$,解得x=4,所以长方形的长为4+4+4+1=13,宽为4+2+4+1=11,面积为13×11=143。因为A的边长为1,故其面积为1,则鼠标落在正方形A内的可能性的大小为$\frac{1}{143}$。

7. (找规律)若一个正整数能表示为两个正整数的平方差,则称这个正整数为"智慧数"(如$3= 2^{2}-1^{2},5= 3^{2}-2^{2}$)。已知"智慧数"按照从小到大的顺序构成如下数列:3,5,7,8,9,11,12,13,15,16,17,19,20,21,23,24,25,…,则第100个"智慧数"是______。136

答案： 136 【解析】根据规律把全部智慧数从小到大可按每三个数分为一组,从第2组开始每组的第一个数依次都是4的倍数。归纳可得第n组的第一个数为4n(n≥2),又因为100=3×33+1,所以第100个智慧数是第34组中的第1个数,从而得到4×34=136。

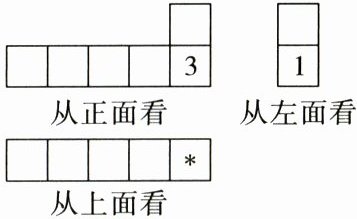
8. (逻辑推理)骰子是6个面上分别写有数字1,2,3,4,5,6的小立方体,它任意两对面上所写的两个数字之和为7。将这样相同的几个骰子按照相接触的两个面上的数字的积为6摆成一个几何体,这个几何体的三视图如图所示。已知图中所标注的是能看到的面上的部分数字,则"*"代表的数字是______。

4

答案： 4 【解析】利用三视图可以得出,这个几何体由6个小正方体组成,从正面看,第一层有5个,第二层有1个,并且在最右端。根据从左面看,下层最左端的正方体左面是1,所以它的对面是6,依次可得,下层最右端的正方体左右面分别是1和6,又根据从正面看,下层最右端的正方体前面是3,则它的对面是4,因此下层最右端正方体上下面分别为2,5,又因为相接触的两个面上的数字的积为6,则下层最右端正方体上面只能为2,上层正方体的下面为3,所以上面为4,故“*”代表的数字为4。

9. (数的认识)一种饼干包装袋上标着:净重$(150\pm 5$克),下面质量不符合要求的是(D)
A.145克
B.150克
C.155克
D.160克

答案： D 【解析】净重(150±5克),表示这种饼干标准的质量是150克,实际每袋最多不多于150+5=155(克),最少不少于150-5=145(克)。所以选项中只有D项160克不符合要求。