《2025年初一入学分班必刷卷六年级数学》

1. (轴对称图形)如图,下面是四个小正方形组成的“L”图形。请你用三种方法,在已知图案上添画一个小正方形后,使其成为一个轴对称图形,并画出对称轴。

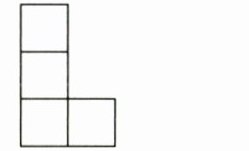
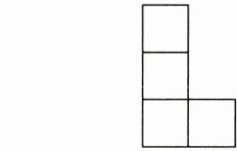
答案：
见解析 【解析】

2. (画变换后的图形)在下面边长为1的方格图中有线段AB,请画出所有使三角形ABC是面积为8的等腰三角形ABC。

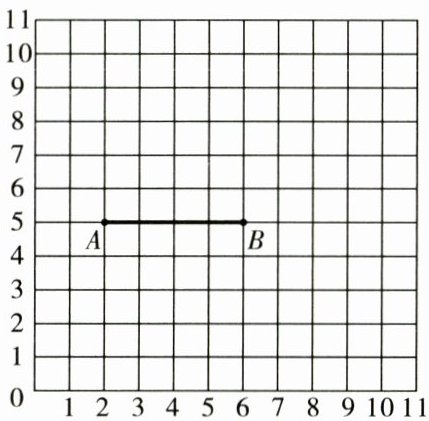
答案：
见解析 【解析】线段AB长为4，所以以AB为边的三角形面积为8时，AB边上的高应是4，在AB的上下两侧各作一条距离AB为4的直线，则所有满足要求的点都应该在这两条直线上，如图所示：

3. (图形的变换与位置)一块正方形的巧克力,猴妈妈先把其中四分之一掰下来孝敬猴王,然后把余下来的平均分给了她的四个孩子(如图所示),每个孩子必须分一整块。她想使得每个孩子获得的巧克力不但面积相同,而且形状也相同。猴妈妈能做到吗?如果不能,请说明理由;如果可以,请你帮猴妈妈画出分割图。

答案：
见解析 【解析】能做到。如图，每个小猴子可分得面积相同且形状相同的巧克力。

4. (旋转的特征)如图,四边形ABCD是长方形,BC= 6cm,AB= 10cm,对角线AC,BD相交于点O。E,F分别是AD与BC的中点,图中阴影部分以EF为轴旋转一周,则白色部分扫出的立体图形的体积是多少立方厘米?(保留π)

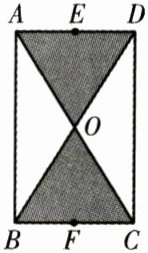
答案：
60π cm³ 【解析】圆柱体的体积为π×$(\frac{6}{2})^2$×10 = 90π(cm³)，两个圆锥体的体积为2×$\frac{1}{3}$π×$(\frac{6}{2})^2$×$\frac{10}{2}$ = 30π(cm³)。
则白色部分扫出的体积为90π - 30π = 60π(cm³)。
答：白色部分扫出的立体图形的体积是60π cm³。