《2025年初一入学分班必刷卷六年级数学》

1. (计数原理)房管员不小心把 11 个房间的 11 把钥匙放混了,若每把钥匙恰好能开启一个房间,则至少试55次才能一定把房间与钥匙配对好。

答案： 55 【解析】11把钥匙开11个房间，要一定能打开，从最坏的情况考虑，若第1把钥匙前10个房间门都打不开，则最后1个房间门不用试肯定能打开，此时第1把钥匙需要试10次。同理可得：第2把钥匙需要试9次，第3把钥匙需要试8次，以此类推，第10把钥匙需要试1次，而最后一把钥匙不用试直接就可以打开。所以至少试$10 + 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 = 55$(次)。

2. (计数原理)现有 1 克、2 克、5 克砝码各一个,那么在天平上能称出7种不同质量的物体。(砝码只能放在一个托盘中)

答案： 7 【解析】只放一个砝码：1克，2克，5克，共3种不同的质量；两个砝码搭配：1克 + 2克 = 3(克)，1克 + 5克 = 6(克)，2克 + 5克 = 7(克)，共3种不同的质量；三个砝码搭配：1克 + 2克 + 5克 = 8(克)，共能称出$3 + 3 + 1 = 7$(种)不同质量的物体。

3. (计数原理)如图,在 10 个空白的正方形中选 1 个(把其余 9 个都剪掉),与分别写有"祝学习进步"字样的 5 个正方形折成一个正方体纸盒,共有4种不同的选法。

答案： 4 【解析】①选“祝”的左面的一个构成“33”型；②分别取“习”，“进”，“步”下面的都构成“132”型。所以共有4种不同的选法。

4. (计数原理)有三个完全相同的立方体,每个立方体的六个面上都分别标有 1~6 这六个数字,那么当任意摆放时,三个立方体向上的三个面的数字之和有16种不同的取值。

答案： 16 【解析】因为1到6数字是连续的，所以我们只需要求出三个面的数字之和为最大的值和最小的值就可以了。三个面的数字之和最小为$1 + 1 + 1 = 3$，三个面的数字之和最大为$6 + 6 + 6 = 18$，不同的取值种数共有$18 - 3 + 1 = 16$(种)。

5. (计数原理)某学校四、五、六三个年级组织了一场文艺演出,共演出 18 个节目,如果每个年级至少演出 4 个节目,那么这三个年级演出节目数的所有不同情况共有 28种。

答案： 28 【解析】$18 - 3×4 = 6$(个)，然后把这6个节目分给三个年级。六年级多出6个，就有1种情况；六年级多出5个节目，有2种情况；六年级多出4个节目，有3种情况；六年级多出3个节目，有4种情况；六年级多出2个节目，有5种情况；六年级多出1个节目，有6种情况；六年级不多出节目，有7种情况。由此可得$1 + 2 + 3 + 4 + 5 + 6 + 7 = 28$(种)情况。

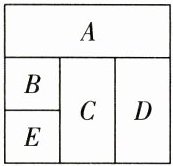
6. (排列组合)如果用 5 种不同的颜色对图中的 A、B、C、D、E 五个区域染色,要求相邻区域染不同的颜色,共有540种染法。

答案： 540 【解析】因为C与其他区域都相连，故先考虑C，C有5种，D有4种，A有3种。当B和D一样时，B有1种，E有3种；当B和D不一样时，B有2种，E有3种。故共有$5×4×3×1×3 + 5×4×3×2×3 = 540$(种)。

7. (排列组合)小学六年级毕业时,小明和班上的 14 位同学都是非常好的朋友,他和这些朋友(包括小明共 15 人)决定组合照相以留作纪念,但只允许一张照片出现三个人,且相同三人只能合影一次,则在他们所有的照片中,小明最多出现 91 次。

答案： 91 【解析】本题要求小明最多出现多少次，并且三人只能合影一次，不能重复。可将问题简化为从14人中选取2人与小明合影，则小明出现的次数最多为$13 + 12 + 11 +... + 1 = \frac{(1 + 13)×13}{2} = 91$(次)。

8. (排列组合)小明有 20 颗糖,其中水果糖 9 颗,巧克力糖 5 颗,夹心糖 6 颗,从中任取 10 颗糖,使得水果糖不少于 2 颗但不多于 8 颗,巧克力糖不少于 2 颗,夹心糖不多于 3 颗,那么符合这种取法的有 种。

答案：
16 【解析】根据题意，则水果糖有7种取法：2，3，4，5，6，7，8；巧克力糖有4种取法：2，3，4，5；夹心糖有4种取法：0，1，2，3。然后根据所取糖的总颗数为10，用枚举法，将所有可能的情况列举出来，如下： 则符合这种取法的有16种。

9. (容斥原理)在一次考试中,某班数学得 100 分的有 17 人,语文得 100 分的有 8 人,两科都得 100 分的有 3 人,那么全班 50 人中两科都没有得 100 分的有28人。

答案： 28 【解析】至少一科得100分的有$17 + 8 - 3 = 22$(人)，两科都没得100分的有$50 - 22 = 28$(人)。

10. (容斥原理)有一根长 240 厘米的绳子,从一端开始每 4 厘米作一个记号,每 6 厘米也作一个记号,然后将标有记号的地方剪断,绳子共被剪成80段。

答案： 80 【解析】4厘米的标记个数为$240÷4 - 1 = 59$(个)，6厘米的标记个数为$240÷6 - 1 = 39$(个)。而4和6的最小公倍数是12，则标记在12厘米及其倍数的地方标记会重合，共有$240÷12 - 1 = 19$(个)，则这根绳子上共有标记数为$59 + 39 - 19 = 79$(个)，所以绳子共被剪成$79 + 1 = 80$(段)。

11. (容斥原理)在 1~500 中,不能被 2 整除,不能被 3 整除,又不能被 7 整除的数有143个。

答案： 143 【解析】被2整除的有$500÷2 = 250$(个)，被3整除的有$500÷3 = 166$(个)……2(个)，被7整除的有$500÷7 = 71$(个)……3(个)。2和3的最小公倍数是6，$500÷6 = 83$(个)……2(个)；3和7的最小公倍数是21，$500÷21 = 23$(个)……17(个)；2和7的最小公倍数是14，$500÷14 = 35$(个)……10(个)；2，3，7的最小公倍数是42，$500÷42 = 11$(个)……38(个)。因此不能被2整除，不能被3整除，不能被7整除的数有$500 - 250 - 166 - 71 + 83 + 23 + 35 - 11 = 143$(个)。

12. (抽屉原理)布袋里有 4 种不同颜色的球(球的大小、质地完全相同),每种都有 10 个,至少取出9个球,才能保证其中一定有 3 个球的颜色相同。

答案： 9 【解析】根据最不利原则可知，要保证其中一定有3个球颜色相同，可每种颜色先取2个，若再取1个，即可出现3个球颜色相同，即$4×2 + 1 = 9$(个)。

13. (抽屉原理)从自然数 1~1000 中最多可以选出334个数,使被选出的数中任意两个数的差都不能整除它们的和。

答案： 334 【解析】将自然数1到999分成333组：1，2，3；4，5，6；7，8，9；……；997，998，999。每组中的数都是三个连续的自然数，任选出其中的两个数，如果这两个数奇偶相同，则和为偶数，差为2；否则，和为奇数，差为1。所以，在某组中任选两个数，它们的差都可以整除它们的和。根据抽屉原理，如果从1~1000中选出的数的个数大于334，必定有两个数在前面所给的333组数的某组中，这样选出的数不满足题目要求。另一方面，当选出1，4，7，……，1000，即选出的数为$3k + 1(k = 0, 1, 2, ..., 333)$时，其中任意两个数的和被3除余2，它们的差是3的倍数，满足题目的要求。所以最多可以选出334个数。