《2025年初一入学分班必刷卷六年级数学》

1. (组合图形的面积)如图,在长方形ABCD中,AD= 6,CD= 4。弧DF和弧DE是分别以A,C为圆心,AD,CD为半径画出来的。求图中阴影部分的面积。(结果保留π)

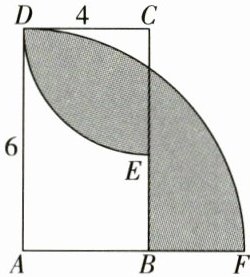
答案： $13\pi - 24$ [解析]$S_{阴}=S_{扇形ADF}+S_{扇形CDE}-S_{长方形ABCD}=\frac{1}{4}×\pi×6^{2}+\frac{1}{4}×\pi×4^{2}-6×4=9\pi + 4\pi - 24=13\pi - 24$
答：图中阴影部分的面积是$13\pi - 24$。

2. (组合图形的面积)如图,在直角三角形ABC的两条直角边AC、BC上分别作正方形ACFE和CBGD,连接DF,连接AG交BC于点P,连接DP,若AC= 12,BC= 26,则△ADP的面积是多少?

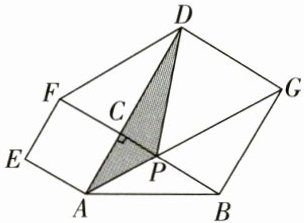
答案： 156 [解析]四边形BCDG是正方形，$S_{\triangle ABC}=\frac{1}{2}S_{正方形BCDG}$，$S_{\triangle DPC}=\frac{1}{2}S_{正方形BCDG}$，因此$S_{\triangle ABC}+S_{\triangle DGP}=S_{正方形BCDG}=S_{\triangle DCF}+S_{\triangle DGP}+S_{\triangle GPB}$，从而得到$S_{\triangle APB}=S_{\triangle DPC}$，△ADP的面积就等于△ABC的面积。$S_{\triangle ADP}=S_{\triangle ABC}=12×26÷2 = 156$。
答：△ADP的面积是156。

3. (组合图形的面积)如图,四边形ABCD是直角梯形,四边形ACFE是长方形,已知BC-AD= 4 cm,CD= 6 cm,梯形面积是$60 cm^2,$求阴影部分的面积。

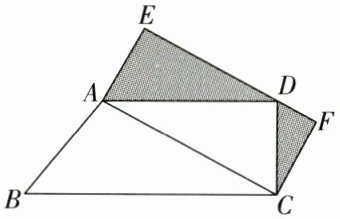
答案： $24\,\text{cm}^2$ [解析]△ADC的面积是$(60 - 6×4÷2)÷2 = 24(\text{cm}^2)$由于△ADC的面积是长方形ACFE面积的一半，故阴影部分的面积等于△ADC的面积，即$24\,\text{cm}^2$。